最新北师大版六年级上册数学整理与复习+五年级数学上册总复习数与代数 72页

整理与复习 北师大版六年级上册 （ 4 ＋ 6 ） ×4 ÷2 =10×4÷2 =20cm 2 （ 4 ÷2 ） 2 × 3.14÷2 =12.56 ÷2 =6.28cm 2 20 —6.28=13.72cm 2 20×20=400cm 2 （ 10÷2 ） 2 × 3.14 =78.5cm 2 400 —78.5=321.5cm 2 小圆半径： 43.96÷3.14÷2=7m 大圆半径： 7 ＋ 3=10m 10 2 × 3.14—7 2 × 3.14 =314—153.86 =160.14cm 2 答 : 这条路的面积是 160.14cm 2 总复习 数与代数 （ 20-10.5 ） ÷2.5=3.8 （元） 倍数与因数 1. 因数和倍数 2. 2、 5 、 3 的倍数的特征 3. 找因数、倍数的方法 4. 质数和合数 重要知识点： 重要概念： 1、一个数的因数的个数是 有限 的，最小的因数是 1 ，最大的因数是 它本身 。 2、一个数的倍数的个数是 无限 的，最小的倍数是 它本身 ，没有最大的倍数。 3、（ ）是任一自然数（0除外）的因数。 4、一个非零自然数的因数最少有（ ）个，这个数是（ ）。比 1 大的任何整数至少有（ ）个因数。 5、一个数的因数都（ ）他本身， 一个数的倍数都（ ）他本身。 6、 一个数的最小倍数=这个数的最大因数=这个数 1 1 两 小于等于 大于等于 1 2 的倍数特征： 5 的倍数特征： 3 的倍数特征： 同时是 2 和 5 的倍数特征： 同时是 3 和 5 的倍数特征： 同时是 2 和 3 的倍数特征： 同时是 2 、 3 、 5 的倍数特征： 个位上是 0 、 2 、 4 、 6 、 8 的数 个位上是 0 或 5 的数 个位上是 0 的数 各个 数位 上的 数字之和 是 3 的倍数的数 2 、 5 、 3 倍数的特征： 个位上是 0 或 5 ，且各个数位上的数字 之和是 3 的倍数 个位上是 0 、 2 、 4 、 6 、 8 ，且各个数位 上的数字之和是 3 的倍数 个位上是 0 ，且各个数位上的数字 之和是 3 的倍数 自然数 ( 是否是 2 的倍数 ) 奇数 偶数 “ 自然数中，除了奇数就是偶数”，这句话对吗？ 奇数和偶数（ 0 也是偶数 ） 1 、在 1 ， 2 ， 15 ， 48 ， 60 ， 13 ， 59 ， 39 中， 2 的倍数有： 3 的倍数有： 5 的倍数有： 是 2 的倍数又是 3 的倍数有： 是 2 的倍数又是 5 的倍数有： 是 3 的倍数又是 5 的倍数有： 既是 2 和 5 的倍数 , 又是 3 的倍数 : 2 ， 48 ， 60 15 ， 48 ， 60 ， 39 15 ， 60 48 ， 60 60 15 ， 60 60 3 、 1 是质数还是合数 ? 为什么 ? 1 既不是质数也不是合数 质数和合数（ 不包括 0 ） 1 、什么是质数（素数）？ 2 、什么是合数？ 一个数，如果除了 1 和它本身还有别的因数，这 样的数叫做合数。 一个数，如果只有 1 和它本身两个因数，这样的数叫做质数（或素数） 自然数 ( 按因数的个数 ) 质数 合数 1 “ 自然数中，除了质数就是合数”，这句话对吗？ 只有两个因数 至少有 3 个因数 2 、最小的质数是（ ），最小的合数是（ ），最小的偶数是（ ），最小的奇数是（ ），一个合数至少有（ ）个因数。 3、1-100各数中，最大的质数是（ ）。 4 、 20 以内，最小的质数与最大的合 数的和是（ ），积是 （ ）。 97 4 22 40 1、 背一背 100 以内质数表 ！ 2 0 1 3 判断 1、因为 2×6=12, 所以 2 是因数 ,12 是倍数 ( ) 2、如果A ÷ B=5，那么A是B的倍数（ ） 3、一个数越大，因数个数越多。（ ） 4、一个自然数不是奇数就是偶数（ ） 5、任何一个合数的因数个数都是偶数个 （ ） × × × × 6、两个质数的乘积一定是合数。（ ） 7 、一个数的因数一定比它的倍数小（ ） 8 、一个数的因数是有限的，倍数是无限的。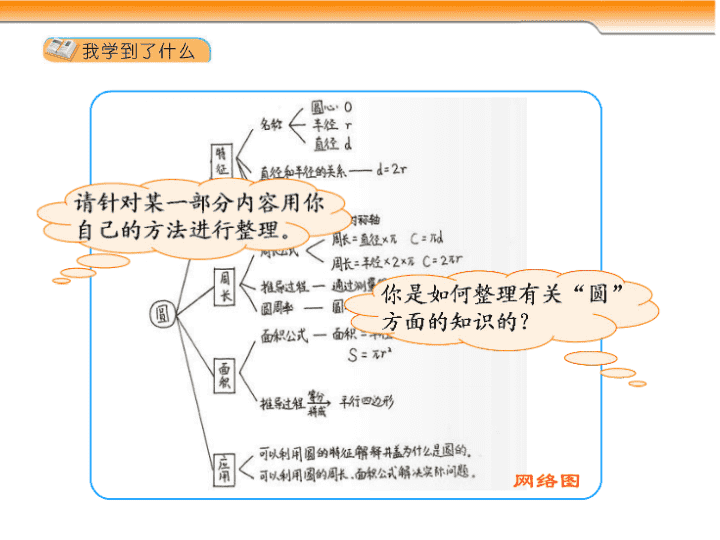 （ ） 9 、 31, 41, 51, 61, 71 都是质数 .( ) × × 密码： ABCDEFGH A 、既是质数又是偶数 B 、 10 以内既是奇数又是合数 C 、只有因数 1 和 7 D 、 10 以内是 2 和 3 的倍数 E 、能被 9 整除的最小一位数 F 、既不是质数也不是合数 G 、最小的合数 H 、既有因数 5 又是 5 的倍数的一位数 密码： 29769145 智破密码 汇总图 分数的意义 看见这两个分数你想起了什么？我们这个单元都学习了一些什么内容？ 分数的意义 分数单位 真分数 分数的基本性质 约分 通分 小数化成分数 分数和小数的互化 分数大小比较 本单元学习的主要内容 分 数 的 意 义 和 性 质 意义 分数的意义，单位“ 1” 的含义 小结：单位“ 1” 与分数单位的区别 单位 “ 1 ” 表示：一个物体、 一些 物体、 一个计量单位或者一个整体。 分数单位表示：把单位 “ 1 ” 平均分成若干份，其中 1 份的数。 本单元学习的主要内容 分 数 的 意 义 和 性 质 意义 分数的意义，单位“ 1” 的含义 分数与除法的关系 小结：分数与除法的关系 分数可以表示整数除法的商，在表示整数除法时，要用除数作分母，用被除数作分子。 用关系式表示： 被除数 ÷ 除数 = ———— 用字母可以表示成： a÷b= —— 因为除数不能等于 “ 0 ” ，所以 b 也不能等于 “ 0 ” 。 被除数 除数 a b 本单元学习的主要内容 分 数 的 意 义 和 性 质 意义 分数的意义，单位“ 1” 的含义 分数与除法的关系 真分数和假分数 带分数的定义 小结：真分数、假分数和带分数 与 1 的关系 真分数小于 1 ； 假分数大于 1 或者等于 1 ； 带分数大于 1 ； 本单元学习的主要内容 分 数 的 意 义 和 性 质 意义 分数的意义，单位“ 1” 的含义 分数与除法的关系 真分数和假分数 性质 带分数的定义 分数的基本性质与商不变的规律 约分 约分的方法 （最大公因数） 通分 通分的方法（最小公倍数） 分数的基本性质 1 、分数的基本性质 分数的分子和分母同时乘上或者除以相同的数（ 0 除外），分数的大小不变。这叫做分数的基本性质。 2 、约分 把一个分数化成同它相等，但分子、分母都比较小的分数，叫做约分。 3 、通分 把异分母分数分别化成和原来分数相等的同分母分数，叫做通分。 4 、最简分数 分子、分母是互质数的分数，叫做最简分数。 第二关：分数的基本性质 2 、比较下面每组中两个分数的大小 3 8 5 8 ○ 1 5 1 7 ○ 5 9 7 12 ○ 1 、把不是最简分数的化简成最简分数 6 8 10 11 7 21 20 70 3 4 = 3 4 1 3 = 1 3 2 7 = 2 7 分母相同 ， 分子大 的分数比较 大 。 分子相同 ， 分母大 的分数比较 小 。 5 9 20 36 = 7 12 21 36 = 20 36 21 36 < < > < 本单元学习的主要内容 分 数 的 意 义 和 性 质 意义 分数的意义，单位“ 1” 的含义 分数与除法的关系 真分数和假分数 性质 带分数的定义 假分数与带分数（整数）的互化 互化 分数和小数的互化 分数的基本性质与商不变的规律 约分 约分的方法 （最大公因数） 通分 通分的方法（最小公倍数） 本单元学习的主要内容 分 数 的 意 义 和 性 质 意义 分数的意义，单位“ 1” 的含义 分数与除法的关系 真分数和假分数 性质 带分数的定义 假分数与带分数（整数）的互化 互化 分数和小数的互化 分数的基本性质与商不变的规律 约分 约分的方法 （最大公因数） 通分 通分的方法（最小公倍数） （ 1 ）假分数一定比 1 大。　　　　（ 　） （ 2 ） 1 米的　 和 4 米　 的一样长。（ 　） （ 3 ）分数的分子和分母同时乘以或除以相同的数，分数的大小不变。　　　 （ 　） （ 4 ）最简分数的分子和分母一定都是质数。　　　　　　　　　　　　　 （ 　 ） （ 5 ）把单位“ 1” 分成若干份，表示这样的 1 份或几份的数，叫做分数。 　　　 （ 　 ） （9 ） 分数单位是 九分之一 的真分数有8 个 。 （ ） × × × × √ 判断。（对的画 “√” ，错的画“ ×” ） √ 扩展题： 一个分数的分母加 4 ，这个分数就等于 —— ，如果在原分数的分子上加 1 ，这 个分数就等于 1 。原分数是几？ 10 11 3 、王师傅 6 分钟加工 14 个零件，李师傅 8 分 钟加工 20 个同样的零件。谁做得比较快？ 方法一： 每分钟加工多少个零件？ 方法二： 每个零件需要多少分钟？ 王： 14÷6 ＝ 李： 20÷8 ＝ ( 个 ) 14 6 20 8 ( 个 ) 2 1 3 1 2 2 2 1 3 1 2 2 < 王： 6÷14 ＝ 李： 20÷8 ＝ ( 分 ) 6 14 8 20 ( 分 ) 3 7 2 5 3 7 2 5 > 每分钟加工多的快，每个零件用时少的快。 答：李师傅做得比较快。 分数 1 、意义 一个、一些物体 平均分 比大小 2 、分类 真分数 ＜ 1 假分数 ≥ 1 带分数 3 、基本性质 加减 约分 4 、分数小数互化 单位 “ 1 ” 分数单位 整数 通分 最简分数 分子、分母 最大公因数 ( 互质数 ) 分母 最小公倍数 同分母分数 一个整体 分数 分母 10 、 100 … 再化简 小数 分子 ÷ 分母 分数 1 、意义 一个、一些物体 平均分 比大小 2 、分类 真分数 ＜ 1 假分数 ≥ 1 带分数 3 、基本性质 加减 约分 4 、分数小数互化 单位 “ 1 ” 分数单位 整数 通分 最简分数 分子、分母 最大公因数 ( 互质数 ) 分母 最小公倍数 同分母分数 一个整体 分数 分母 10 、 100 … 再化简 小数 分子 ÷ 分母 小数除法 小数除以整数 例： 5.07÷6 ） 5.07 6 0 . 8 4 8 2 7 4 24 3 =0.845 小数除以整数的计算方法： （ 1 ）按 整数除法 的方法去除 （ 2 ） 商 的小数点要和 被除数 的小数点对齐 （ 3 ）整数部分 不够除 ， 商 0 ， 点上小数点 （ 4 ）如果 有余数 , 要 添 0 再除 0 5 30 0 除数是小数 例： 12.6÷0.28 （ 1 ）怎样写竖式 （ 2 ）接下来怎么算 除数是小数的计算方法： （ 2 ）按 整数除法 的方法去除 （ 3 ） 商 的小数点要和 被除数 的小数点对齐 （ 4 ）整数部分 不够除 ， 商 0 ， 点上小数点 （ 5 ）如果 有余数 ，要 添 0 再除 把 除数 变成 整数 , 被除数和 除数 同时扩大相同 的倍数 ） 12.6 0.28 （ 1 ）用 商不变 定律 被除数位数不够 , 用 0 补足 例： 12.6÷0.28 0.28 12.6 例： 12.6÷0.28 0.28 被除数位数不够 , 用 0 补足 12.6 例： 12.6÷0.28 0.28 13.5 ÷ 30 1 0.3 被除数（ ），除数（ ） 1 ，商（ ）被除数。 除数（ ） 1 ，商（ ）被除数。 除数（ ） 1 ，商（ ）被除数。 = 商的变化规律 13.5 45 不变 大于 小于 等于 等于 小于 大于 0.45 在（ ）里填上 “ ＞” “＜” 说说你的理由 4.48÷3.5 （ ） 4.48 12.3÷1.5 （ ） 12.3 13.3÷0.95 （ ） 13.3 7.2÷0.64 （ ） 7.2 ＜ ＜ ＞ ＞ ÷0. 12 5 0.5 0.05 = 0.5 计算下面两组题，你发现了什么？把发现写在下面的横线上。 5 50 0.48 4.8 48 = 4 2.5 ÷ 40 400 ⑴ 被除数不变，除数缩小，商扩大 . ⑵ 除数不变 , 被除数扩大 , 商扩大 . 求商的近似值，一般先除到比需要保留的小数位数 多一位 ，再按照“ 四舍五入 ”法取商的近似值 。 商的近似数 7.14545 … 5.33 … 1.555 … 一个小数的 小数部分 ，从 某一位 起，一个数字或者几个数字 依次不断重复出现 ，这样的小数叫 循环小数 。 概括规律 循环小数 依次不断重复出现的数字是？ 6 2438 47 2 一个循环小数的小数部分，依次重复出现的数字，叫做循环小数的 循环节 。 3.4666 （ ） 0.2 4382438 （ ） 8.4747 （ ） 0.44222 （ ） … … … … 继续探索 15:1 ， 15 ， 3 ， 5 。 36:1 ， 36 ， 2 ， 18 ， 3 ， 12 ， 4 ， 9 。 3: 3 ， 6 ， 9 ， 12 ， 15,18,21,24,27,30,33,36,39,42,45,48 。 8: 8 ， 16 ， 24 ， 32 ， 40 ， 48 。 8 、 28 、 10 、 90 、 100 90 、 45 25 、 10 、 90 、 45 、 100 240÷120=2 120÷240=0.5= 3÷6= =0.5 （千克） 5 7 3 3 8 25 < > > < 480 10 32 . 0.0 6 . . 0.42 （ 52.9-30.5 ） ÷4=5.6 （元） 86.1÷3=28.7 （米） 6.4m=64dm 64÷1.4=40 （个） 3.9×2×2=15.6 （千米） 28.8÷0.6=48 （本） 48÷2=24 （只）