小学数学精讲教案3_2_9 接送问题 学生版 9页

接送问题 教学目标 ‎1、准确画出接送问题的过程图——标准：每个量在相同时间所走的路程要分清 ‎2、理解运动过程，抓住变化规律 ‎3、运用行程中的比例关系进行解题 知识精讲 一、 校车问题——行走过程描述 队伍多，校车少，校车来回接送，队伍不断步行和坐车，最终同时到达目的地，即到达目的地的最短时间，不要求证明。‎ 二、常见接送问题类型 根据校车速度（来回不同）、班级速度（不同班不同速）、班数是否变化分类为四种常见题型：‎ ‎（1）车速不变-班速不变-班数2个（最常见） （2）车速不变-班速不变-班数多个 （3）车速不变-班速变-班数2个 （4）车速变-班速不变-班数2个 三、标准解法：‎ 画图＋列3个式子 ‎1、总时间=一个队伍坐车的时间+这个队伍步行的时间；‎ ‎2、班车走的总路程；‎ ‎3、一个队伍步行的时间=班车同时出发后回来接它的时间。‎ 模块一、汽车接送问题——接一个人 【例 1】 某校和某工厂之间有一条公路，该校下午2时派车去该厂接某劳模来做报告，往返需用1小时．这位劳模在下午1时便离厂步行向学校走来，途中遇到接他的汽车，便立刻上车驶向学校，在下午2时40分到达．问：汽车速度是劳模步行速度的几倍？‎ 【巩固】 张工程师每天早上点准时被司机从家接到厂里。一天，张工程师早上点就出了门，开始步行去厂里，在路上遇到了接他的汽车，于是，他就上车行完了剩下的路程，到厂时提前分钟。这天，张工程师还是早上点出门，但分钟后他发现有东西没有带，于是回家去取，再出门后在路上遇到了接他的汽车，那么这次他比平常要提前 分钟到厂。‎ 【例 1】 李经理的司机每天早上7点30分到达李经理家接他去公司。有一天李经理7点从家里出发去公司，路上遇到从公司按时来接他的车，再乘车去公司，结果比平常早到5分钟。则李经理乘车的速度是步行速度的 倍。（假设车速、步行速度保持不变，汽车掉头与上下车时间忽略不计）‎ 模块二、汽车接送问题——接两个人或多人 ‎（一）、车速不变、人速不变 【例 2】 ‎（难度级别 ※※※）A、B两个连队同时分别从两个营地出发前往一个目的地进行演习，A连有卡车可以装载正好一个连的人员，为了让两个连队的士兵同时尽快到达目的地，A连士兵坐车出发一定时间后下车让卡车回去接B连的士兵，两营的士兵恰好同时到达目的地，已知营地与目的地之间的距离为‎32千米，士兵行军速度为‎8千米/小时，卡车行驶速度为‎40千米每小时，求两营士兵到达目的地一共要多少时间？‎ 【巩固】 甲班与乙班学生同时从学校出发去公园，两班的步行速度相等都是千米/小时，学校有一辆汽车，它的速度是每小时千米，这辆汽车恰好能坐一个班的学生．为了使两班学生在最短时间内到达公园，设两地相距千米，那么各个班的步行距离是多少？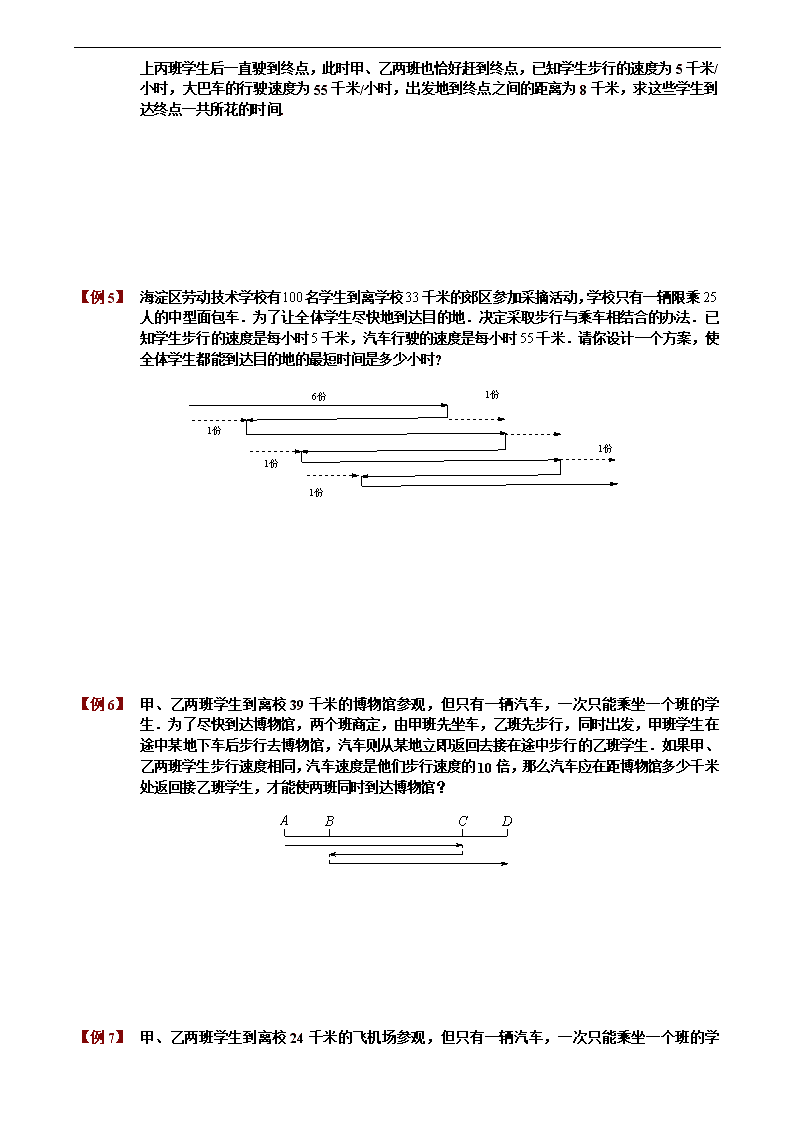‎ 【例 3】 ‎（难度级别 ‎ ‎※※）甲、乙、丙三个班的学生一起去郊外活动，他们租了一辆大巴，但大巴只够一个班的学生坐，于是他们计划先让甲班的学生步行，乙丙两班的学生步行，甲班学生搭乘大巴一段路后，下车步行，然后大巴车回头去接乙班学生，并追赶上步行的甲班学生，再回头载上丙班学生后一直驶到终点，此时甲、乙两班也恰好赶到终点，已知学生步行的速度为‎5千米/小时，大巴车的行驶速度为‎55千米/小时，出发地到终点之间的距离为‎8千米，求这些学生到达终点一共所花的时间.‎ 【例 1】 海淀区劳动技术学校有名学生到离学校千米的郊区参加采摘活动，学校只有一辆限乘人的中型面包车．为了让全体学生尽快地到达目的地．决定采取步行与乘车相结合的办法．已知学生步行的速度是每小时千米，汽车行驶的速度是每小时千米．请你设计一个方案，使全体学生都能到达目的地的最短时间是多少小时?‎ 【例 2】 甲、乙两班学生到离校‎39千米的博物馆参观，但只有一辆汽车，一次只能乘坐一个班的学生．为了尽快到达博物馆，两个班商定，由甲班先坐车，乙班先步行，同时出发，甲班学生在途中某地下车后步行去博物馆，汽车则从某地立即返回去接在途中步行的乙班学生．如果甲、乙两班学生步行速度相同，汽车速度是他们步行速度的10倍，那么汽车应在距博物馆多少千米处返回接乙班学生，才能使两班同时到达博物馆？‎ 【例 3】 甲、乙两班学生到离校‎24千米 的飞机场参观，但只有一辆汽车，一次只能乘坐一个班的学生．为了尽快到达飞机场，两个班商定，由甲班先坐车，乙班先步行，同时出发，甲班学生在途中某地下车后步行去飞机场，汽车则从某地立即返回接在途中步行的乙班学生．如果甲、乙两班学生步行速度相同，汽车速度是他们步行速度的7倍，那么汽车应在距飞机场多少千米处返回接乙班学生，才能使两班同时到达飞机场?‎ 【例 1】 ‎、两地相距千米．有一支游行队伍从出发，向匀速前进；当游行队伍队尾离开时，甲、乙两人分别从、两地同时出发．乙向步行；甲骑车先追向队头，追上队头后又立即骑向队尾，到达队尾后再立即追向队头，追上队头后又立即骑向队尾……当甲第次追上队头时恰与乙相遇在距地千米处；当甲第次追上队头时，甲恰好第一次到达地，那么此时乙距地还有__________千米．‎ 【例 2】 ‎、两地相距千米．有一支游行队伍从出发，向匀速前进；当游行队伍队尾离开时，甲、乙两人分别从、两地同时出发．乙向步行；甲骑车先追向队头，追上队头后又立即骑向队尾，到达队尾后再立即追向队头，追上队头后又立即骑向队尾……当甲第5次追上队头时恰与乙相遇在距地‎5.6千米处；当甲第7次追上队头时，甲恰好第一次到达地，那么此时乙距地还有______千米．‎ ‎（二）车速不变、人速变 【例 3】 ‎（难度级别 ※※）甲班与乙班学生同时从学校出发去公园，甲班步行的速度是每小时4千米，乙班步行的速度是每小时3千米。学校有一辆汽车，它的速度是每小时48千米，这辆汽车恰好能坐一个班的学生。为了使两班学生在最短时间内到达公园，那么甲班学生与乙班学生需要步行的距离之比是多少千米？‎ ‎（三）、车速变、人速不变 【例 1】 甲、乙两班同学到‎42千米外的少年宫参加活动，但只有一辆汽车，且一次只能坐一个班的同学，已知学生步行速度相同为千米／小时，汽车载人速度是千米／小时，空车速度是千米/小时．如果要使两班同学同时到达，且到达时间最短，那么这个最短时间是多少？‎ 【例 2】 有两个班的小学生要到少年宫参加活动，但只有一辆车接送，第一班的学生坐车从学校出发的同时，第二班学生开始步行；车到途中某处，让第一班学生下车步行，车立刻返回接第二班学生上车并直接开往少年宫，学生步行速度为每小时4公里，载学生时车速每小时40公里，空车时车速为每小时50公里．问：要使两班学生同时到达少年宫，第一班学生要步行全程的几分之几？‎ 【例 3】 某学校学生计划乘坐旅行社的大巴前往郊外游玩，按照计划，旅行社的大巴准时从车站出发后能在约定时间到达学校，搭载满学生在预定时间到达目的地，已知学校的位置在车站和目的地之间，大巴车空载的时候的速度为千米/小时，满载的时候速度为千米/小时，由于某种原因大巴车晚出发了分钟，学生在约定时间没有等到大巴车的情况下，步行前往目的地，在途中搭载上赶上来的大巴车，最后比预定时间晚了分钟到达目的地，求学生们的步行速度．‎ ‎（四）、车速变、人速变 【例 4】 ‎（台湾小学数学竞赛选拔赛决赛）甲、乙二人由地同时出发朝向地前进，、两地之距离为千米．甲步行之速度为每小时千米，乙步行之速度为每小时千米．现有一辆自行车，甲骑车速度为每小时千米，乙骑车的速度为每小时千米．出发时由甲先骑车，乙步行，为了要使两人都尽快抵达目的地，骑自行车在前面的人可以将自行车留置在途中供后面的人继续骑．请问他们从出发到最后一人抵达目的地最少需要多少小时？‎ 模块三、汽车接送问题——借车赶路问题 【例 1】 ‎（难度级别 ※※※※※）三个人同时前往相距‎30千米的甲地，已知三人行走的速度相同，都是‎5千米每小时；现在还有一辆自行车，但只能一个人骑，已知骑车的速度为‎10千米每小时。现先让其中一人先骑车，到中途某地后放车放下，继续前进；第二个人到达后骑上再行驶一段后有放下让最后那人骑行，自己继续前进，这样三人同时到达甲地。问，三人花的时间各为多少？‎ 【例 2】 ‎(全国“华罗庚金杯”少年数学邀请赛)、两地相距120千米，已知人的步行速度是每小时‎5千米，摩托车的行驶速度是每小时50千米，摩托车后座可带一人．问：有三人并配备一辆摩托车从地到地最少需要多少小时？(保留—位小数)‎ 【例 3】 兄弟两人骑马进城，全程‎51千米。马每时行‎12千米，但只能由一个人骑。哥哥每时步行‎5千米，弟弟每时步行‎4千米。两人轮换骑马和步行，骑马者走过一段距离就下鞍拴马（下鞍拴马的时间忽略不计），然后独自步行。而步行者到达此地，再上马前进。若他们早晨6点动身，则何时能同时到达城里？‎ 【巩固】 ‎（难度级别 ※）甲乙两人同时从学校出发去距离‎33千米外的公园，甲步行的速度是每小时4千米，乙步行的速度是每小时3千米。他们有一辆自行车，它的速度是每小时5千米，这辆车只能载一个人，所以先让其中一人先骑车到中途，然后把车放下之后继续前进，等另一个人赶到放车的位置后再骑车赶去，这样使两人同时到达公园。那么放车的位置距出发点多少千米？‎ 【巩固】 ‎、两人同时自甲地出发去乙地，、步行的速度分别为米/分、米/分，两人骑车的速度都是米/分，先骑车到途中某地下车把车放下，立即步行前进；走到车处，立即骑车前进，当超过一段路程后，把车放下，立即步行前进，两人如此继续交替用车，最后两人同时到达乙地，那么从甲地到乙地的平均速度是 米/分．‎ 【例 1】 A、B两地相距30千米，甲乙丙三人同时从A到B，而且要求同时到达。现在有两辆自行车，但不许带人，但可以将自行车放在中途某处，后来的人可以接着骑。已知骑自行车的平均速度为每小时20千米，甲步行的速度是每小时‎5千米，乙和丙每小时‎4千米，那么三人需要多少小时可以同时到达？‎ 【例 2】 设有甲、乙、丙三人，他们步行的速度相同，骑车的速度也相同，骑车的速度是步行速度的倍．现甲从地去地，乙、丙从地去地，双方同时出发．出发时，甲、乙为步行，丙骑车．途中，当甲、丙相遇时，丙将车给甲骑，自己改为步行，三人仍按各自原有方向继续前进；当甲、乙相遇时，甲将车给乙骑，自己重又步行，三人仍按各自原有方向继续前进．问：三人之中谁最先达到自己的目的地？谁最后到达目的地？‎ 模块四、汽车接送问题——策略问题 【例 3】 两辆同一型号的汽车从同一地点同时出发，沿同一方向同速直线前进，每车最多能带20桶汽油（连同油箱内的油）。每桶汽油可以使一辆汽车前进‎60千米，两车都必须返回出发地点，两辆车均可借对方的油，为了使一辆车尽可能地远离出发点，那么这辆车最远可达到离出发点多少千米远的地方？‎ 【巩固】 ‎（难度等级 ※※※※）在一个沙漠地带，汽车每天行驶‎200千米，每辆汽车载运可行驶24天的汽油．现有甲、乙两辆汽车同时从某地出发，并在完成任务后，沿原路返回．为了让甲车尽可能开出更远的距离，乙车在行驶一段路程后，仅留下自己返回出发地的汽油，将其他的油给甲车．求甲车所能开行的最远距离．‎ 【例 1】 一个旅游者于是10时15分从旅游基地乘小艇出发，务必在不迟于当日13时返回。已知河水速度为‎1.4千米/小时，小艇在静水中的速度为‎3千米/小时，如果旅游者每过30分钟就休息15分钟，不靠岸，只能在某次休息后才返回，那么他从旅游基地出发乘艇走过的最大距离是＿＿＿＿千米。‎ 【例 2】 某沙漠通讯班接到紧急命令，让他们火速将一份情报送过沙漠。现在已知沙漠通讯班成员只有靠步行穿过沙漠，每个人步行穿过沙漠的时间均为12天，而每个人最多只能带8天的食物，请问，在假定每个人饭量大小相同，且所能带的食物相同的情况下，沙漠通讯班能否完成任务？如果能，那么最少需要几人才能将情报送过沙漠，怎么送？‎ 【例 3】 甲、乙两人要到沙漠中探险，他们每天向沙漠深处走‎20千米，已知每人最多可携带一个人24天的食物和水．⑴ 如果不准将部分食物存放在途中，问其中一人最远可以深人沙漠多少千米（当然要求二人最后返回出发点）？⑵ 如果可以将部分食物存放于途中以备返回时取用，情况又怎样呢？‎ 【例 1】 有5位探险家计划横穿沙漠．他们每人驾驶一辆吉普车，每辆车最多能携带可供一辆车行驶‎312千米的汽油．显然，5个人不可能共同穿越‎500千米以上的沙漠．于是，他们计划在保证其余车完全返回出发点的前提下，让一辆车穿越沙漠，当然实现这一计划需要几辆车相互借用汽油．问：穿越沙漠的那辆车最多能穿越多宽的沙漠？‎ 【例 2】 ‎（小学数学奥林匹克决赛试题）科学考察队的一辆越野车需要穿越一片全程大于千米的沙漠，但这辆车每次装满汽油最多只能驶千米，队长想出一个方法，在沙漠中设一个储油点，越野车装满油从起点出发，到储油点时从车中取出部分油放进储油点，然后返回出发点，加满油后再开往，到储油点时取出储存的油放在车上，从出发点到达终点．用队长想出的方法，越野车不用其他车帮助就完成了任务，那么，这辆越野车穿越这片沙漠的最大行程是 千米．‎ 【例 3】 ‎ (北大附中“资优博雅杯”数学竞赛)有一只小猴子在深山中发现了一片野香蕉园，它一共摘了根香蕉，然后要走米才能到家，如果它每次最多只能背根香蕉，并且它每走米就要吃掉一根香蕉，那么，它最多可以把 根香蕉带回家？‎