六年级下册数学试题 小升初数学模拟试卷（五）全国通用 PDF 含答案 4页

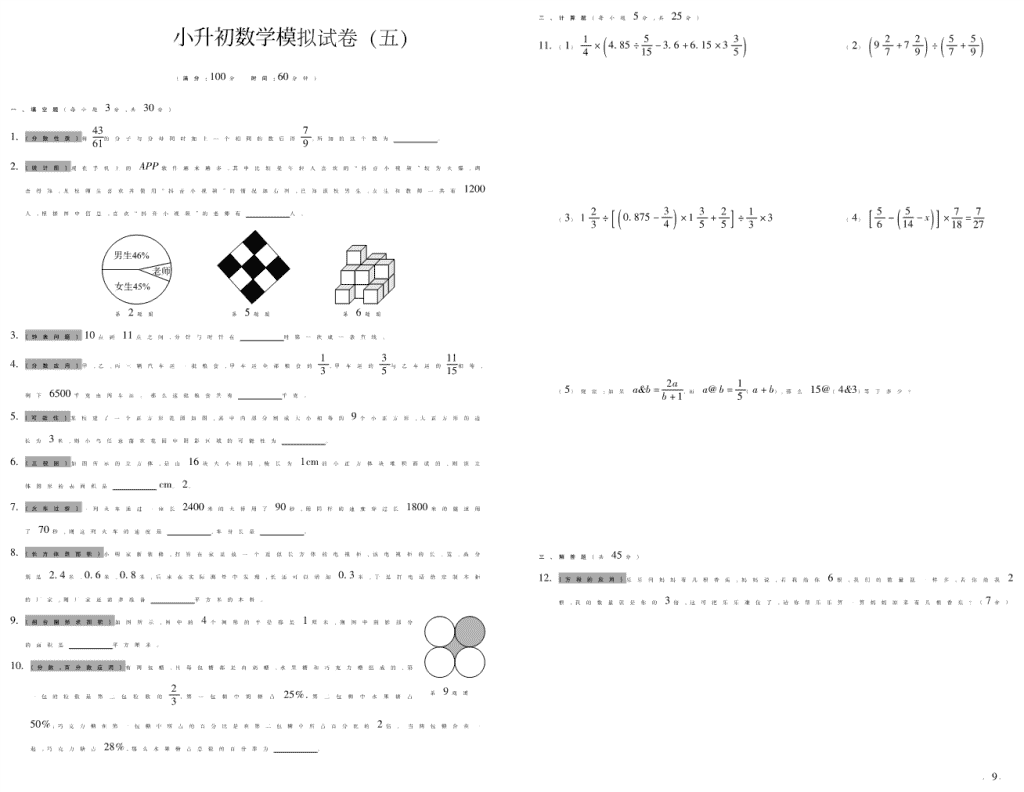
小升初数学模拟试卷（五） （满分：１００分　时间：６０分钟） 一、填空题（每小题 ３分，共 ３０分） １．（分数性质）将４３ ６１的分子与分母同时加上一个相同的数后得 ７ ９，所加的这个数为 。 ２．（统计图）现在手机上的 ＡＰＰ软件越来越多，其中比较受年轻人喜欢的“抖音小视频”较为火爆，调 查得知，某校师生喜欢并使用“抖音小视频”的情况如右图，已知该校男生、女生和教师一共有 １２００ 人，根据图中信息，喜欢“抖音小视频”的老师有 人。 第 ２题图 　　　　 第 ５题图 　　　　 第 ６题图 ３．（钟表问题）１０点到 １１点之间，分针与时针在 时第一次成一条直线。 ４．（分数应用）甲、乙、丙三辆汽车运一批粮食，甲车运全部粮食的 １ ３，甲车运的 ３ ５与乙车运的１１ １５相等， 剩下 ６５００千克由丙车运。那么这批粮食共有 千克。 ５．（可能性）某校建了一个正方形花园如图，其中内部分割成大小相等的 ９个小正方形，大正方形的边 长为 ３米，则小鸟任意落在花园中阴影区域的可能性为 。 ６．（三视图）如图所示的立方体，是由 １６块大小相同，棱长为 １ｃｍ的小正方体块堆积而成的，则该立 体图形的表面积是 ｃｍ。２。 ７．（火车过桥）一列火车通过一座长 ２４００米的大桥用了 ９０秒，用同样的速度穿过长 １８００米的隧道用 了 ７０秒，则这列火车的速度是 ，车身长是 。 ８．（长方体表面积）小明家新装修，打算在家里放一个近似长方体的电视柜，该电视柜的长、宽、高分 别是 ２．４米、０．６米、０．８米，后来在实际测量中发现，长还可以增加 ０．３米，于是打电话给定制木柜 的厂家，则厂家还需多准备 平方米的木料。 第 ９题图 ９．（组合圈形求面积）如图所示，图中的 ４个圆形的半径都是 １厘米，则图中阴影部分 的面积是 平方厘米。 １０．（分数、百分数应用）有两包糖，且每包糖都是由奶糖、水果糖和巧克力糖组成的，第 一包的粒数是第二包粒数的 ２ ３，第一包糖中奶糖占 ２５％．第二包糖中水果糖占 ５０％；巧克力糖在第一包糖中所占的百分比是在第二包糖中所占百分比的 ２倍。当两包糖合在一 起，巧克力糖占 ２８％，那么水果糖占总数的百分率为 。 二、计算题（每小题 ５分，共 ２５分） １１．（１）１ ４× ４．８５÷５ １５－３．６＋６．１５×３( )３ ５ 　　　　　　　　　（２） ９２ ７＋７( )２ ９ ÷ ５ ７＋( )５ ９ （３）１２ ３÷ ０．８７５－( )３ ４ ×１３ ５＋[ ]２ ５ ÷１ ３×３ （４） ５ ６－ ５ １４－( )[ ]ｘ ×７ １８＝７ ２７ （５）规定：如果 ａ＆ｂ＝ ２ａ ｂ＋１，而 ａ＠ｂ＝１ ５（ａ＋ｂ），那么 １５＠（４＆３）等于多少？ 三、解答题（共 ４５分） １２．（方程的应用）乐乐问妈妈有几根香蕉，妈妈说，若我给你 ６根，我们的数量就一样多，若你给我 ２ 根，我的数量就是你的 ３倍，这可把乐乐难住了，请你帮乐乐算一算妈妈原来有几根香蕉？（７分） ·９· １３．（圆柱表面积）一张长方形铁皮，如图剪下阴影部分刚好制成圆柱体（单位：分米），求这个圆柱体 的表面积？（π取 ３．１４）（７分） 第 １３题图 １４．（水管问题）甲、乙两个长方体水池装满了水，两水池的高相等。已知甲池的排水管 １０分钟可将水 排完，乙池的排水管 ６分钟可将水排完。问：同时打开甲、乙两池的排水管，多长时间后甲池的水 位高正好是乙池水位高的 ３倍？（７分） １５．（底高模型）如图所示，在△ＡＢＣ中，ＣＰ＝１ ２，ＣＱ＝１ ３ＣＡ，ＢＱ与 ＡＰ相交于点 Ｘ，若△ＡＢＣ的面积为 ６，则△ＡＢＸ的面积等于多少？（８分） 第 １５题图 １６．（行程问题）乐乐和玲玲同时从家里出发相向而行。玲玲每分钟走 ５２米，乐乐每分钟走 ７０米，两 人在途中 Ａ处相遇。若玲玲提前 ４分钟出发，且速度不变，乐乐每分钟改为走 ９０米，则两人仍在 Ａ处相遇。问玲玲和乐乐两人的家相距多少米？（８分） １７．（方程组的应用）莱工厂购进 Ａ、Ｂ两种品牌的设备，通过再加工然后售出，这两种设备的进价和销 售如下表所示： Ａ Ｂ 进价（万元／套） １．５ １．２ 售价（万元／套） １．６５ １．４ 该工厂计划购进两种设备若干套，共需 ６６万元，全部销售后可获毛利润 ９万元。［毛利润 ＝（售价 －迸价）×销售量］（８分） （１）该工厂计划购进 Ａ、Ｂ两种品牌的设备各多少套？ （２）通过市场调研，该工厂决定在原计划的基础上，减少 Ａ种设备的购进数盘，增加 Ｂ种设备的购 进数量，已知 Ｂ种设备增加数量是 Ａ种设备减少数量的 １．５倍，若用于购进这两种设备的总 资金不超避 ６９万元，则 Ａ种设备购进数量至多减少多少套？ ·０１· 小升初数学模拟试卷（五） 一、１．２０ 【解析】设所加的数为 ｘ，则４３＋ｘ ６１＋ｘ＝７ ９，解得 ｘ＝ ２０，因此所加的这个数为 ２０。 ２．１０８ 【解析】因为该校男生、女生和教师一共有 １２００人， 而根据扇形统计图中男生和女生占的百分比可知， 老师占：１－４６％ －４５％ ＝９％，所以喜欢“抖音小视 频”的老师有 １２００×９％ ＝１０８（人）。 ３．１０点 ２１９ １１分 【解析】时针每分钟走 ０．５°，分针每分钟走 ６°，１０点 时分针与时针的夹角是 ２×３０°＝６０°，设走 ｘ分时， 分针与删针笫一次在一条直线上，则 ６ｘ－０．５ｘ＝ １８０°－６０°，解褂 ｘ＝２１ ９ １１，即分针与时针在 １０点 ２１９ １１分时第一次成一条直线。 ４．１６５００ 【解析】乙运了全部粮食的 １ ３ ×３ ５ ÷１１ １５＝３ １１，根根量 率对应可知这批粮食共有 ６５００÷ １－１ ３ －３( )１１ ＝ １６５００（千克）。 ５．５ ９ 【解析】由题图可知，大正方形的面积是 ３×３＝９（平 方米），而题图中将大正方形分成 ９个大小相等的小 正方形，即每个小正方形的而积是 ９÷９＝１（平方 米），题图中有 ５个阴影小正方形，所以小岛落在阴 影区域的概率是 ５÷９＝５ ９。 ６．５０ 【解析】该立方体由 １６个小立方体组成，其从前面可 以看到 ７个小正方形，从左面可以看到 ９个小正方 形，从上面也同样的可以看到 ９个面，根据这三个面 可以看到的小正方形的个数可以得出，外立方体的 外表面一共有（７＋９＋９）×２＝５０（个）面，则可的该 立方体的表面积是 １×１×５０＝５０（ｃｍ２）。 ７．３０米／秒 ３００米 【解析】该列火车通过两座不同长度的桥所用时间不 同，则可计算出火车的速度是（２４００－１８００）÷（９０－ ７０）＝３０（米／秒），再利用车速可得车长是 ３０×９０－ ２４００＝３００（米）。 ８．０．８４ 【解析】原电视拒是近似的长方体，原长方体的长增 加了 ０．３米，则长方体增加了 ４个面，即两个长是 ０．６米，宽是 ０．３米的面和两个长为 ０．８米，宽为 ０．３ 米的面，所以厂家还需多准备 （０．３×０．６＋０．３× ０．８）×２＝０．８４（平方米）的木料。 ９．４ 【解析】将四个圆中间部分所求的阴 影部分分别沿圆的交点连线分成四 份，如解图所示，则阴影部分面积即 为 ４个小正方形的面积，所以阴影部分的面积是 ４× １×１＝４（平方厘米）。 １０．４４％ 【解析】第一包糖的粒数是第二包的 ２ ３，可设第一包 糖的粒数是 ２，第二包糖的粒数是 ３，则第一包中的 奶糖是 ２×２５％ ＝０．５，第二包糖中的水果精是 ３× ５０％ ＝１．５，两包糖的巧克力糖是（２＋３）×２８％ ＝ １．４，第一、第二包糖的巧克力糖的比是（２×２）∶（３ ×１）＝４∶３，则第一包中的巧克力糖的粒数是 １．４÷ （４＋３）×４＝０．８，所以第一包中的水果糖是 ２－０．５ －０．８＝０．７，则两包中水果糖占总数的（１．５＋０．７） ÷（２＋３）×１００％ ＝４４％。 二、 １１．（１）解：原式 ＝１ ４×（４．８５×３．６－３．６＋６．１５×３．６） ＝１ ４ ×３．６×（４．８５－１＋６．１５） ＝０．９×１０ ＝９ （２）解：原式 ＝ ６５ ７ ＋６５( )９ ÷ ５ ７ ＋( )５ ９ ＝ ６５× １ ７ ＋( )１ ９ ５× １ ７ ＋( )１ ９ ＝１３ （３）解：原式 ＝５ ３ ÷ ７ ８ －( )３ ４ ×８ ５ ＋[ ]２ ５ ×３×３ ＝５ ３ ÷ １ ８ ×８ ５ ＋[ ]２ ５ ×３×３ ＝５ ３ ×５ ３ ×３×３ ＝２５ （４） ５ ６ － ５ １４－( )[ ]ｘ ×７ １８＝７ ２７ 解： ５ ６ －５ １４＋ｘ＝７ ２７÷７ １８ ３５ ４２－１５ ４５＋ｘ＝２ ３ １０ ２１＋ｘ＝２ ３ ｘ＝４ ２１ （５）按题中规定的新运算顺宁得 ４＆３＝２×４ ３＋１＝２， 所以 １５＠（４＆３）＝１５＠２＝１ ５ ×（１５＋２）＝３２ ５。 三、１２．解：设妈妈原来有香蕉 ｘ根，则乐乐原来有香蕉 ｘ－６－６根，根据题意可列方程为：ｘ＋２＝３（ｘ －６－６－２），解得：ｘ＝２２。 答：妈妈原来有 ２２根香蕉。 １３．解：圆柱底面直径：１８．８４÷３．１４＝６（分米）， 圆柱的高：１０－６＝４（分米）， 圆柱的表面积：１８．８４×４＋３．１４×（６÷２）２ ×２＝ １３１．８８（平方分米）。 答：这个圆柱体的表面积为 １３１．８８平方分米。 １４．解：设甲长方体水池的底面积为 Ｓ１，乙长方体水池 的底面积为 Ｓ２，刚开始的高度为 １，ｘ分钟后甲池的 水位高正好是乙池水位高的 ３倍。 则 Ｓ１ －ｘ １０Ｓ１ Ｓ１ ＝３× Ｓ２ －ｘ ６Ｓ２ Ｓ２ ， 解得：ｘ＝５。 答：５分钟后甲池的水位高正好是乙池水位商的 ３倍。 １５．解：如解图所示，连接 ＰＱ。 由于 ＣＰ＝ １ ２ＣＢ，ＣＱ＝ １ ３ ＣＡ，所以 Ｓ△ＡＢＰ ＝ １ ２Ｓ△ＡＢＣ， Ｓ△ＡＢＱ ＝２ ３Ｓ△ＡＢＣ，Ｓ△ＰＣＱ ＝１ ３Ｓ△ＡＢＣ，所以 Ｓ△ＢＰＱ ＝１ ２ Ｓ△ＢＣＱ ＝１ ６Ｓ△ＡＢＣ。由蝴蝶定理知，ＡＸ∶ＸＰ＝Ｓ△ＡＢＱ∶ Ｓ△ＢＰＱ ＝２ ３Ｓ△ＡＢＣ∶１ ６Ｓ△ＡＢＣ ＝４∶１，所以 Ｓ△ＡＢＸ ＝ ４ ５ Ｓ△ＡＢＰ ＝４ ５ ×１ ２Ｓ△ＡＢＣ ＝２ ５Ｓ△ＡＢＣ ＝２ ５ ×６＝２．４。 答：三角形 ＡＢＸ的面积等于 ２．４。 １６．解：原来玲玲和乐乐速度比为 ５２∶７０＝２６∶３５， 即相遇时乐乐走了全程的 ３５ ２６＋３５＝３５ ６１， 后来玲玲和乐乐的速度比为 ５２∶９０＝２６∶４５，相遇时 乐乐同样走了全程的３５ ６１， 则玲玲在与乐乐同时走的时问里，行了全程的３５ ６１× ２６ ４５＝１８２ ５４９，……玲玲提前 ４分钟走，而走了 ４分钟， 共走了 ５２×４＝２０８（米）， 两家相距 ２０８÷ １－３５ ６１－１８２( )５４９ ＝２１９６（米）。 答：玲玲和乐乐家相距 ２１９６米。 １７．解：（１）设该工厂计划购进 Ａ、Ｂ两种品牌的设备分 别为 ｘ套，ｙ套。 １．５ｘ＋１．２ｙ＝６６ （１．６５－１．５）ｘ＋（１．４－１．２）ｙ{ ＝９ ，解得 ｘ＝２０ ｙ{ ＝３０ 。 答：该工厂计划购进 Ａ品牌设备 ２０套，Ｂ品牌设备 ３０套。 （２）设 Ａ种设备购进数量减少 ａ套，Ｂ种设备购进 数量增加 １．５ａ套。 １．５（２０－ａ）＋１．２（３０＋１．５ａ）≤６９，解得 ａ≤１０。 答：Ａ种设备购进数量至多减少 １０套。