上海中考数学初三相似三角形讲义 12页

‎ 陈老师家庭课堂辅导讲义 年 级：初三 辅导科目： 数学 ‎ 学生姓名： 辅导老师： 陈相远 课 题 相似三角形复习1‎ 教学目的 教学内容 第一部分： 概念梳理 ‎1、相似形 ‎2、在四条线段中，如果其中两条线段的比等于另外两条线段的比，那么这四条线段叫做成比例线段，简称比例线段.‎ ‎3、比例的性质：‎ ‎ 等比性质、合比性质 ‎4、黄金分割、重心 ‎5、三角形一边的平行线的性质定理 ‎6、三角形一边的平行线的判定定理 ‎7、相似三角形的判定预备定理：‎ ‎8、相似三角形的判定定理 ‎9、相似三角形的性质定理 ‎10、向量的概念 ‎11、向量的线性运算 ‎12、向量的线性组合和分解 第二部分：基础小测验（自己分配时间，也可以课下测验）‎ ‎（时间：20--30分钟，总分：100分，每题5分）‎ 选择题 ‎1、东海大桥全长32.5千米，如果东海大桥在某张地图上的长为6.5厘米，那么该地图上距离与实际距离的比为（ ）．‎ A．1：5000000； B．1：500000； C．1：50000； D．1：5000． ‎ ‎2、根据你对相似的理解，下列命题中，不正确的是（ ）．‎ ‎（A）两个全等三角形一定相似； （B）两个等边三角形一定相似；‎ ‎（C）两个直角三角形一定相似； （D）两个正方形一定相似．‎ ‎3、如果（其中），那么下列式子中不正确的是（ ）‎ A． ； B． ； C． ； D． ．‎ ‎4、下列四个命题中，真命题的个数为………………………………（ ）‎ ‎（1）平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似；‎ ‎（2）如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似；‎ ‎（3）如果一个三角形的两边与其中一条边上的中线与另一个三角形的两边及其中一条边上的中线对应成比例，那么这两个三角形相似； ‎ ‎（4）如果一个三角形的两边及第三边上的高与另一个三角形的两边及第三边上的高对应成比例，那么这两个三角形相似.‎ ‎（A）1个； （B）2个； （C）3个； （D）4个.‎ ‎5．如图5，在△ABC中，点D、E分别在边AB、AC上，DE//BC，AD∶BD = 1∶2，那么S△DBE∶S△CBE等于（ ）‎ ‎（A）1∶2； （B）1∶3； （C）1∶4； （D）1∶6．‎ ‎6．已知非零向量和单位向量，则下列等式中正确的是( ) ．‎ A. B. C. D. ‎ ‎7．如图，已知∥∥，，那么下列结论正确的是（ ）‎ ‎（A）；（B）；‎ B A C D ‎8题图 ‎（C）；（D）．‎ A B C D E F ‎7题图 A C D E ‎（5题图）‎ ‎8．如图，在中，，，点在腰上，且，那么下列结论正确的是（ ）‎ ‎（A）；（B）；（C）；（D）．‎ G A B D C O ‎9、如图，梯形ABCD的对角线AC、BD相交于O，G是BD的中点．‎ 若AD = 3，BC = 9，则GO : BG =（ ）．‎ A．1 : 2 B．1 : 3‎ C．2 : 3 D．11 : 20‎ ‎ ‎ ‎10、若△ABC∽△DEF, △ABC与△DEF的相似比为１∶2，则△ABC与△DEF的周长比为（ ）‎ A．1∶4 B．1∶‎2 ‎ C．2∶1 D．１∶‎ ‎11、在△ABC中，AB=12，AC=10，BC=9，AD是BC边上的高.将△ABC按如图所示的方式折叠，使点A与点D 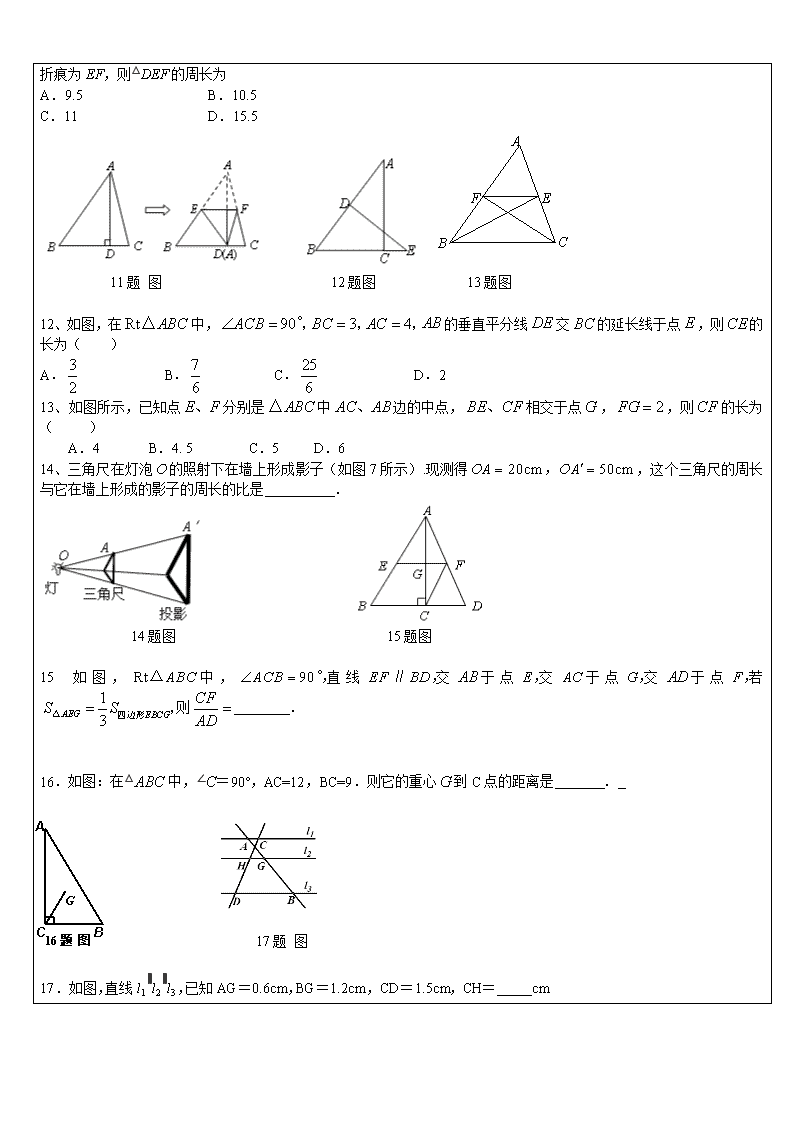重合，折痕为EF，则△DEF的周长为 A．9.5 B．10.5‎ C．11 D．15.5‎ ‎ ‎A F E C B ‎ 11题 图 12题图 13题图 ‎12、如图，在中，的垂直平分线交的延长线于点，则的长为（ ）‎ A． B． C． D．2‎ ‎13、如图所示，已知点分别是中边的中点，相交于点，，则的长为（ ）‎ A．4 B．4. 5 C．5 D．6 ‎ ‎14、三角尺在灯泡的照射下在墙上形成影子（如图7所示）.现测得，这个三角尺的周长与它在墙上形成的影子的周长的比是 ．‎ ‎ ‎ ‎ 14题图 15题图 ‎15如图，中，直线交于点交于点交于点若则 ．‎ ‎16．如图：在△ABC中，∠C＝90°，AC=12，BC=9．则它的重心到C点的距离是 ． ‎ ‎16题 图 ‎ 17题 图 ‎17．如图，直线l1∥l2∥l3，已知AG＝‎0.6cm，BG＝‎1.2cm，CD＝‎1.5cm，CH＝_____cm ‎18.如图，已知在平行四边形ABCD中，点E、F分别在线段 BD、AB上，EF∥AD，DE∶EB=2∶3，EF=9，那么BC的长为 ．‎ D A B C B F E ‎18题图 ‎ ‎ ‎19题 ‎19如图，已知AD∥EF∥BC，且AE＝2EB，AD＝‎8 cm，AD＝‎8 cm，BC＝‎14 cm，‎ 则S梯形A。EFD︰S梯形BCFE＝____________．‎ ‎20将三角形按照如图所示的方式折叠，使点B落在边AC上，记为点B′，折痕为EF．若以点B′，F，C为顶点的三角形与△ABC相似，那么BF的长度是 ．‎ ‎20题图 ‎【请呗忘记总结回顾】‎ 第三部分：综合题分析 ‎1、如图，在△ABC中，点D、E分别在BC、AC上，BE平分∠ABC，‎ ‎ DE∥BA． 如果CE=24， AE=26， AB=45，求DE和CD的长．‎ A E D B C 第21题 2、 已知，在△ABC中，点D、E分别在AB、AC上，且，‎ 已知，求 ‎3、如图，在△ABC中，D是AB的中点，过点D的直线交边AC于E，交BC的延长线于F，‎ 求证：‎ ‎4、如图，在△ABC中,AB=AC,D、E分别是AC及AC延长线上的点,连接BD、BE,已知AC2=AD•AE，‎ 求证:（1）△ＡＢＤ∽△ＡＥＢ．（2）BC平分∠DBE.‎ ‎ ‎ ‎ ‎ ‎5、已知：AD是Rt△ABC中∠A的平分线，∠C=90°，EF是AD的垂直平分线交AD于M，EF、BC的延长线交于 一点N。求证：(1)△AME∽△NMD (2)ND2=NC·NB ‎ ‎ ‎ ‎6、在和中, ·＝·,＝,＝4.‎ 求证∶＝2.‎ ‎7、如图，M为线段AB的中点，AE与BD交于点C，∠DME＝∠A＝∠B＝α，‎ 且DM交AC于F，ME交BC于G．‎ ‎（1）写出图中三对相似三角形，并证明其中的一对；‎ ‎（2）连结FG，如果α＝45°，AB＝，AF＝3，求FG的长．‎ ‎【关键词】直角三角形的有关计算、相似三角形有关的计算和证明 ‎【答案】‎ ‎（1）证：△AMF∽△BGM，△DMG∽△DBM，△EMF∽△EAM（写出两对即可）‎ 以下证明△AMF∽△BGM．‎ ‎∵∠AFM＝∠DME＋∠E＝∠A＋∠E＝∠BMG，∠A＝∠B ‎∴△AMF∽△BGM． ‎ ‎（2）解：当α＝45°时，可得AC⊥BC且AC＝BC ‎∵M为AB的中点，∴AM＝BM＝分 又∵AMF∽△BGM，∴‎ ‎∴ ‎ 又，∴，‎ ‎∴ ‎ ‎8、（本题12分）如图1,在平行四边形中,.‎ ‎ （1）求证：；‎ ‎（2）若点、分别为边、上的两点,且.(如图2)‎ ‎① 求证:∽；‎ F E D C B A ‎ ② 求证:.‎ D C B A ‎ （图1） （图2）‎ ‎9、如图，已知梯形中，//，，，，．‎ 点在边上运动（点不与点、点重合），一束光线从点出发，沿的方向射出，经反射后，反射光线交射线于点．‎ ‎ （1）当 时，求的长度；‎ ‎ （2）当点落在线段上时，设，，试求y与x之间的函数关系，并写出其定义域；‎ ‎（3）联结，若以点、、为顶点的三角形与相似，试求的长度．‎ A D B ‎(备用图）‎ A D B C E P ‎【请别忘记总结回顾】‎ 课外作业：‎ ‎1、（本题满分12分，每小题满分各6分）‎ A M B 第23题图 C E F G 如图，已知：在Rt△ABC中，∠ACB=90°,AC=BC=4， M是边AB的中点，E、G分别是边AC、BC上的一点，∠EMG＝45°,AC与MG的延长线相交于点F，‎ ‎（1）在不添加字母和线段的情况下写出图中一定相似的三角形，并证明其中的一对；‎ ‎（2）联结结EG，当 AE＝3时，求EG的长．‎ ‎2、(2009年义乌)如图，在矩形ABCD中，AB=3,AD=1,点P在线段AB上运动，设AP=，现将纸片折叠，使点D与点P重合，得折痕EF（点E、F为折痕与矩形边的交点），再将纸片还原。‎ ‎ ‎ ‎（1）当时，折痕EF的长为 ；当点E与点A重合时，折痕EF的长为 ；‎ ‎（2）请写出使四边形EPFD为菱形的的取值范围，并求出当时菱形的边长；‎ ‎（3）令，当点E在AD、点F在BC上时，写出与的函数关系式。当取最大值时，判断△EAP与△PBF是否相似？若相似，求出的值；若不相似，请说明理由。‎ 温馨提示：用草稿纸折折看，或许对你有所帮助哦！‎ ‎【关键词】相似三角形 ‎【答案】‎ 解：（1）3， ‎ ‎（2）．‎ D C B A P E F 图1‎ 当时，如图1，连接，‎ 为折痕，，‎ 令为，则，‎ 在中，，‎ ‎，‎ D C F B A P E O 图2‎ H 解得，此时菱形边长为．‎ ‎（3）如图2，过作，‎ 易证，‎ ‎，‎ D C ‎(F)‎ H B A P E O 图3‎ 当与点重合时，如图3，连接，‎ ‎，，‎ ‎．‎ 显然，函数的值在轴的右侧随的增大而增大，‎ 当时，有最大值．‎ 此时，．‎ 综上所述，当取最大值时，，（不写不扣分）．‎