初三中考数学典型的四边形专题训练 5页

中考数学：四边形试题 一、选择题 ‎1.把矩形ABCD沿EF对折后使两部分叠合，如图所示．若，则∠1= （ ） ‎ A.50° B.55° C.60° D.65°‎ ‎（第1题图）‎ ‎1‎ ‎2.如图，直角梯形ABCD中，AB⊥CD，AE∥CD交BC于E，O是AC的中点，，，，下列结论：①∠CAE=30°；②四边形ADCE是菱形；③；④OB⊥CD.其中正确的结论是（ ）‎ A．①②④ 　　B. ②③④ 　　C．①③④ 　　 D．①②③④‎ Ａ Ｂ Ｅ Ｏ Ｄ Ｃ 第2题图 ‎3.如图，ABCD、CEFG是正方形，E在CD上，直线BE、DG交于H，且HE·HB＝，BD、AF交于M，当E在线段CD（不与C、D重合）上运动时，下列四个结论：① BE⊥GD；② AF、GD所夹的锐角为45°；③ GD=；④ 若BE平分∠DBC，则正方形ABCD的面积为4.其中正确的结论个数有（ ）‎ A. 1个B. 2个C. 3个D. 4个 ‎4．如图，把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置，若∠EFB＝65°，则∠AED′等于（　　）‎ A．50°　 B．55°　 C．60°　 D．65°‎ ‎5.如图将矩形ABCD沿DE折叠，使A点落在BC上的F处，若∠EFB＝600，则∠CFD＝（ ）‎ A、200 B、‎300 C、400 D、500‎ ‎6．下列命题中真命题是 （ ）‎ A.有一组邻边相等的四边形是菱形； B.四条边都相等的四边形是菱形； ‎ C.对角线互相垂直的四边形是菱形； D.对角线互相平分且相等的四边形是菱形．‎ ‎7.两条对角线互相垂直平分的四边形是 （ ）.‎ A.等腰梯形； B.菱形； C.矩形； D.平行四边形. ‎ ‎8．如图,四边形ABCD为矩形纸片,将纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF,若CD=6,则AF=( )‎ A:4 B:‎3‎ ‎ C:4 D:8‎ ‎9.如图，正方形ABCD的三边中点E、F、G。连ED交AF于M,‎ GC交DE于N,下列结论　①GM⊥CM ②CD=CM ‎ ‎③四边形MFCG为等腰梯形。　④∠CMD=∠AGM 其中正确的有（　　）‎ A ①②③ 　 B ①②④ 　 C ①③④ 　D ①②③④ ‎ ‎10.如图，已知平行四边形ABCD中，，‎ 于，于，相 交于，的延长线相交于，下面结论：‎ ‎①②③‎ ‎④.其中正确的结论是（ ）‎ A．①②③④ B．①②③ ‎ C．①②④ D．②③④‎ ‎11.（武汉中考命题）如图，直线BD是四边形ABCD的对称轴，已知∠BAD＝120°，∠CDB＝25°，则∠ABC的度数为（ ）‎ A、70° B、60° C、50° D、80°‎ ‎12．如图，Rt△ABC和Rt△CDE中，∠A=30°,‎ ‎∠E=45°,AB=CE,∠BCD=30°,FG⊥AB,下列结论：‎ ‎①CH=FH；②BC=GC；③四边形BDEF为平行四边形；‎ ‎④FH=GF+BH.其中正确的结论是（ ）‎ A．①②③ B．①②④ C．①③④ D．②③④‎ 二、填空题 ‎1.在梯形ABCD中，AD // BC，E、F分别是两腰AB、CD的中点，如果AD = 4，EF = 6，那么BC =____．‎ ‎2.在四边形ABCD中，如果AB∥CD，AB=BC，要使四边形ABCD是菱形，还需添加一个条件，这个条件可以是 . 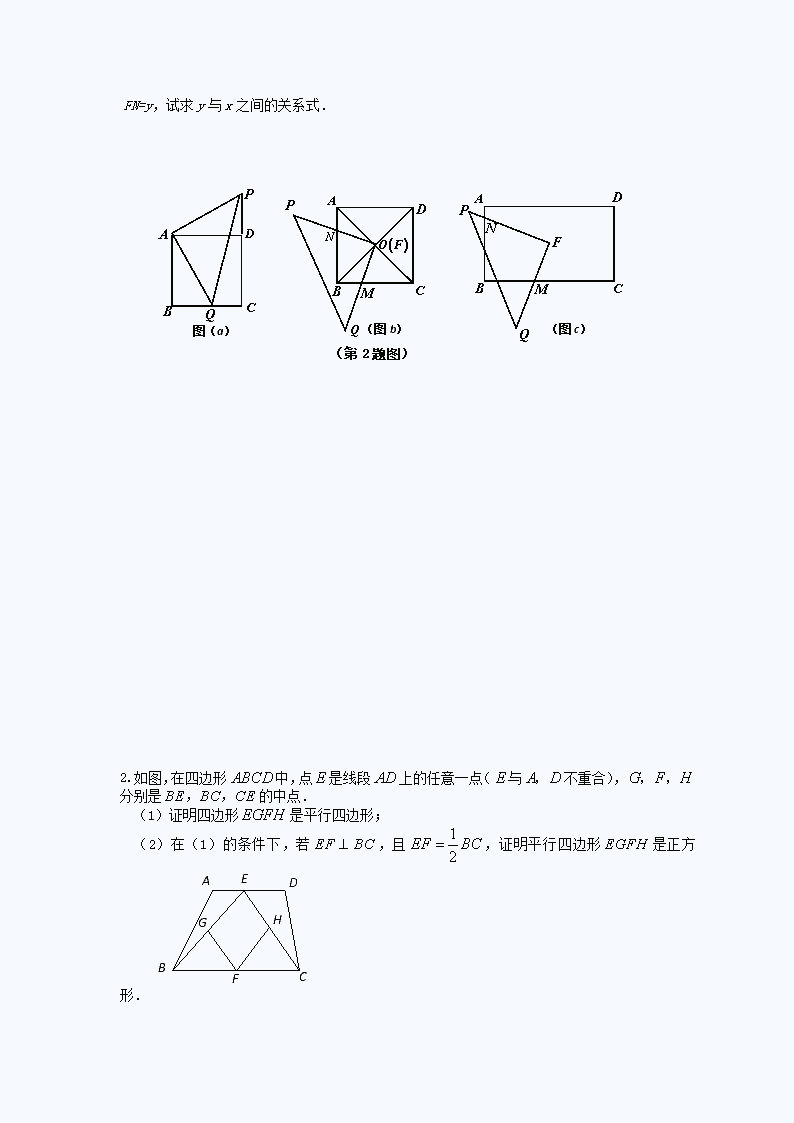‎ ‎3.如图，□ABCD中，∠B＝60°，AB=4,BC=5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是 ‎ ‎4.一个正方形的面积是‎9a2–‎6a+1（a>1），则该正方形的边长是 .‎ 三、解答题 ‎1.一次数学兴趣活动，小明提出这样三个问题，请你解决：‎ ‎（1）把正方形ABCD与等腰Rt△PAQ如图（a）所示重叠在一起，其中∠PAQ=90°，‎ 点Q 在边BC上，连接PD，求证：△ADP≌△ABQ．‎ ‎（2）如图（b），O为正方形ABCD对角线的交点，将一直角三角板FPQ的直角顶点F与点O重合，转动三角板使两直角边始终与BC、AB相交于点M、N，求证：OM=ON．‎ ‎（3）如图（c），将（2）的“正方形”改为“矩形”，其它条件不变，如果AB=4，AD=6，FM=x，‎ FN=y，试求y与x之间的关系式．‎ ‎ ‎ 图（a）‎ ‎（第2题图）‎ ‎（图b）‎ ‎（图c）‎ ‎2.如图，在四边形中，点是线段上的任意一点（与不重合），分别是的中点．‎ ‎（1）证明四边形是平行四边形；‎ ‎（2）在（1）的条件下，若，且，证明平行四边形是正方形．‎B G A E F H D C ‎（（第7题图）‎ A B D C G O E F ‎3.已知：如图，在四边形ABCD中，点G在边BC的延长线上，CE平分∠BCD、CF平分∠GCD， EF∥BC交CD于点O ．‎ ‎（1）求证：OE=OF；‎ ‎（2）若点O为CD的中点，求证：四边形DECF是矩形．‎ ‎4.如图，在△ABC中，D是BC边上的一点，E是AD的 中点，过A点作BC的平行线交CE的延长线于点F，且 AF=BD，连结BF.‎ A F E B D C ‎⑴求证：BD=CD；‎ ‎⑵如果AB=AC，试判断四边形AFBD的形状，‎ 并证明你的结论.‎ ‎5．如图，四边形ABCD中，AD∥BC，对角线AC，BD交于点O，且OA=OC，求证四边形ABCD是平行四边形。‎ ‎6．已知：如图模1-13，在□ABCD中，AE是BC边上的高，将△ABE沿BC方向平移，使点E与点C重合，得△GFC.‎ ‎⑴求证：BE=DG；‎ A D G C B F E ‎⑵若∠B=60°，当AB与BC满足什么数量关系时，四边形ABFG是菱形？证明你的结论.‎ ‎7. 如图,已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上，直线BE与DM交于点N.求证：BN⊥DM A M F D E N B C ‎8. 已知Q是正方形ABCD中CD边上一点,P是BC边上一点;‎ (1) 若∠DAQ=∠PAQ,求证:AP=BP+QD;‎ (2) 若AP=BP+QD,则∠DAQ=∠PAQ成立吗？为什么？‎ A B C D Q P