安徽中考数学试题及答案 7页

安徽省2010年初三毕业生学业考试 数 学 试 题 一、选择题（本大题共10小题，每小题4分，满分40分）‎ 每小题都给出代号为A、B、C、D的四个选项，其中只有一个是正确的，请把正确选项的代号写在题后的括号内，每一小题，选对得4分，不选、选错或选出的代号超过一个的（不论是否写在括号内）一律得0分）‎ ‎1、在－1，0，1，2这四个数中，既不是正数也不是负数的是（ ）‎ ‎ A、－1 B、‎0 ‎‎ C、1 D、2‎ ‎2、计算的结果正确的是（ ）‎ ‎3‎ ‎2‎ ‎1‎ ‎ A、 B、 C、 D、‎ ‎3、如图，直线∥，，，则为（ ）‎ ‎ A、 B、 C、 D、‎ ‎4、2010年第一季度，全国城镇新增就业人数为289万人，用科学记数法表示289万正确的是（ ）‎ ‎ A、 B、 C、 D、‎ ‎5、如图，下列四个几何体中，其主视图、左视图、俯视图中只有两个相同的是（ ）‎ ‎100‎ ‎110‎ ‎115‎ ‎120‎ ‎130‎ ‎140‎ 利润/万元 月份 ‎5‎ ‎4‎ ‎3‎ ‎2‎ ‎1‎ ‎0‎ ‎ A、正方体 B、球体 C、直三棱柱 D、圆柱 ‎6、某企业1～5月份利润的变化情况如图所示，以下说法与图 中反映的信息相符的是（ ）‎ ‎ A、1～2月份利润的增长快于2～3月份利润的增长。‎ B、1～4月份利润的极差与1～5月份利润的极差不同。‎ C、1～5月份利润的众数是130万元。‎ D、1～5月份利润的中位数是120万元。‎ ‎7、若二次函数配方后为，则、的值分别为（ ）‎ A B C O ‎ A、0，5 B、0，‎1 ‎‎ C、－4，5 D、－4，1‎ ‎8、如图。⊙O过点B、C，圆心O在等腰直角△ABC内部，，‎ ‎，，则⊙O的半径为（ ）‎ ‎ A、 B、 C、 D、‎ ‎9、下面两个多位数1248624……，6248624……，都是按照如下方法得到的：将第1位数字乘以2，若积为一位数，将其写在第2位;若积为两位数，则将其个位数字写在第2位，对第2位数字再进行如上操作得到第3位数字……‎ ‎，后面的每一位数字都是由前一位数了进行如上操作得到的，当第1位数字是3时，仍按如上操作得到一个多位数，则这个多位数前100位的所有数字之和是（ ）‎ ‎ A、495 B、‎497 ‎‎ C、501 D、503‎ ‎10、甲、乙两人准备在一段长为‎1200m的笔直公路上进行跑步，甲、乙跑步的速度分别为‎4m/s和‎6m/s，起跑前乙在起点，甲在乙前面‎100m处，若同时起跑，则两人从起跑至其中一人先到达终点的过程中，甲、乙两人之间的距离y（m）与时间t（s）函数图象是（ ）‎ y/m ‎300‎ ‎100‎ ‎275‎ O t/s ‎50‎ y/m ‎300‎ ‎100‎ ‎275‎ O t/s ‎100‎ y/m ‎300‎ ‎100‎ ‎200‎ O t/s ‎50‎ t/s y/m ‎300‎ ‎100‎ ‎200‎ O ‎100‎ A O D B C ‎ A、 B、 C、 D、‎ 二、填空题（本大题共4小题，每小题5分，满分20分）‎ ‎11、计算：______________。‎ ‎12、不等式组的解集是______________。‎ A B C D ‎13、如图，△ABC内接于于⊙O，AC是⊙O的直径，，点D是弧BAC上一点，则_________。‎ ‎14、如图，AD是△ABC的边BC上的高，由下列条件中的某一个就 能推出△ABC是等腰三角形的是_____________（把所有正确答 案的序号都填写在横线上）‎ ‎ ①; ②;‎ ‎③;④;‎ 三、（本大题共2小题，每小题8分，满分16分）‎ ‎15、先化简，再求值。‎ ‎，其中 ‎16、若河岸的两边平行，河宽为‎900米，一只船由河岸的A处沿直线方向开往对岸的B处，AB与河岸的夹角是，船的速度为‎5米/秒，求船从A处到B处的需时间几分。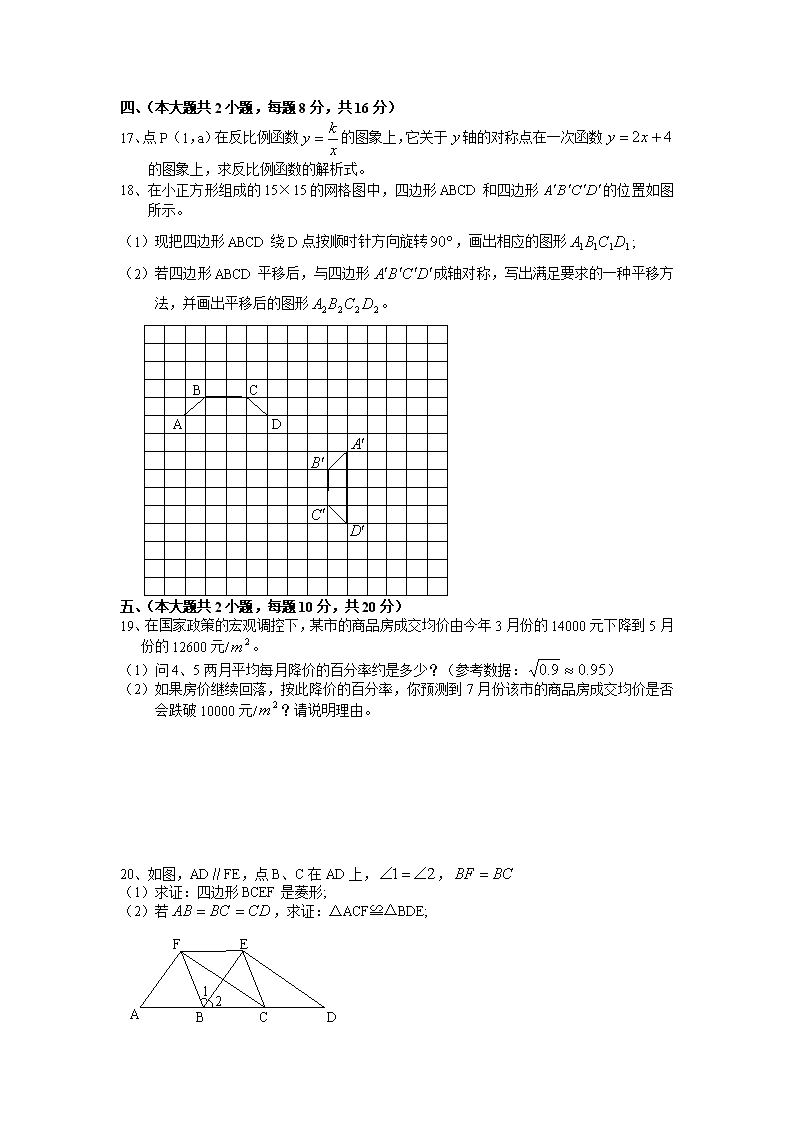（参考数据：）‎ B A 四、（本大题共2小题，每题8分，共16分）‎ ‎17、点P（1，a）在反比例函数的图象上，它关于轴的对称点在一次函数的图象上，求反比例函数的解析式。‎ ‎18、在小正方形组成的15×15的网格图中，四边形ABCD和四边形的位置如图所示。‎ ‎（1）现把四边形ABCD绕D点按顺时针方向旋转，画出相应的图形;‎ ‎（2）若四边形ABCD平移后，与四边形成轴对称，写出满足要求的一种平移方法，并画出平移后的图形。‎ B A C D 五、（本大题共2小题，每题10分，共20分）‎ ‎19、在国家政策的宏观调控下，某市的商品房成交均价由今年3月份的14000元下降到5月份的12600元/。‎ ‎（1）问4、5两月平均每月降价的百分率约是多少？（参考数据：）‎ ‎（2）如果房价继续回落，按此降价的百分率，你预测到7月份该市的商品房成交均价是否会跌破10000元/？请说明理由。‎ ‎20、如图，AD∥FE，点B、C在AD上，，‎ ‎（1）求证：四边形BCEF是菱形;‎ ‎（2）若，求证：△ACF≌△BDE;‎ F A B C D E ‎1‎ ‎2‎ 六、（本题满分12分）‎ ‎21、上海世博会门票的价格如下表示：‎ 门票价格一览表 指定日普通票 ‎200元 平日优惠票 ‎100元 ‎……‎ ‎……‎ 某旅行社准备了1300元，全部用来购买指日普通票和平日优惠票，且每种票至少买一张。‎ ‎（1）有多少种购票方案？列举所有可能结果;‎ ‎（2）如果从上述方案中任意选一种方案购票，求恰好选到11张门票的概率。‎ 七、（本题满分12分）‎ ‎22、春节期间某水库养殖场为适应市场需求，连续用20天时间，采用每天降低水位以减少捕捞成本的办法，对水库中某种鲜鱼进行捕捞、销售。‎ ‎（1）九（1）班数学建模兴趣小组根据调查，整理出第天（且为整数）的捕捞与销售的相关信息如下：‎ 鲜鱼销售单价（元/kg）‎ ‎20‎ 单位捕捞成本（元/kg）‎ 捕捞量（kg）‎ ‎（1）在此期间该养殖场每天的捕捞量与前一天的捕劳量相比是如何变化的？‎ ‎（2）假定该养殖场每天捕捞和销售的鲜鱼没有损失，且能在当天全部售出，求第天的收入（元）与（天）之间的函数关系式;（当天收入＝日销售额－日捕捞成本）‎ ‎（3）试说明（2）中的函数随的变化情况，并指出在第几天取得最大值，最大值是多少？‎ 八、（本题满分14分）‎ ‎23、如图，已知△ABC∽△，相似比为（），且△ABC的三边长分别为、、（），△的三边长分别为、、。‎ ‎（1）若，求证：‎ ‎（2）若，试给出符合条件的一对△ABC和△，使得、、和、、都是正整数，并加以说明;‎ ‎（3）若，，是否存在△ABC和△，使得？请说明理由。‎ B1‎ A1‎ C1‎ b1‎ a1‎ c1‎ A B C c a b 安徽省2010年初中毕业生学业考试 数学试题参考答案 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B A C B D C D C A C 二、填空题 题号 ‎11‎ ‎12‎ ‎13‎ ‎14‎ 答案 ‎②③④‎ 三、解答题 ‎15、解：‎ 当时，原式 ‎16、解：如图，过点B作BC垂直河岸，垂足为C，则在Rt△ACB中，有 B A C ‎ 因而时间.4（分）‎ 即船从A处到B处约需3.5分 ‎17、解：点P（1，）关于轴的对称点是（－1，）‎ ‎ ∵点（－1，）在一次函数的图象上，‎ ‎∴‎ ‎ ∵点P（1，2）在反比例函数的图像上，∴‎ ‎ ∴反比例函数的解析式为 ‎18、解：（1）旋转后得到的图形如图所示 ‎ （2）将四边形ABCD先向右平移4个单位，‎ 再向下平移6个单位，四边形如图所示 B A C D1‎ B2‎ A1‎ B1‎ C1‎ A2‎ C2‎ D2‎ D ‎19、（1）解：设4、5两月平均每月降价的百分率为，‎ 根据题意，得 ‎ ‎ ‎ 化简，得 ‎ 解得：，‎ ‎（不合题意，舍去）‎ ‎ 因此，4，5两月平均每月降价的百分率 约为5％。‎ ‎（2）解：如果按此降价的百分率继续回落，估计7月份的商品房成交均价为 ‎ ‎ ‎ 由此可知，7月份该市的商品房成交均价不会跌破10000元/‎ ‎20、（1）证：∵AD∥EF，∴‎ ‎ ∵，∴‎ ‎ ∴‎ ‎ ∵，∴‎ ‎ ∴四边形BCEF是平行四边形 ‎ ∵‎ ‎ ∴四边形BCEF是菱形。‎ ‎（2）证：∵，，AD∥EF ‎ ∴四边形ABEF、四边形CDEF均为平行四边形，∴，‎ ‎ 又∵‎ ‎ ∴△ACF≌△BDE ‎21、（1）解：有6种购票方案 购票方案 指定日普通票张数 平日优惠票张数 一 ‎1‎ ‎11‎ 二 ‎2‎ ‎9‎ 三 ‎3‎ ‎7‎ 四 ‎4‎ ‎5‎ 五 ‎5‎ ‎3‎ 六 ‎6‎ ‎1‎ ‎（2）解：由（1）知，共有6种购票方案，且选到每种方案的可能性相等，而恰好选到11张门票的方案只有1种，因此恰好选到11张门票的概率是。‎ ‎22、（1）解：该养殖场每天的捕捞量与前一天的捕捞量相比每天减少了‎10kg ‎（2）解：由题意得 ‎ ‎ ‎（3）解：∵，‎ ‎ 又且为整数 ‎ ∴当时，随的增大而增大 ‎ 当时，随的增大而减小 ‎ 当时即在第10天，取得最大值，最大值为14450元 ‎23、（1）证：∵△ABC∽△，且相似比为（），∴，∴‎ ‎ 又∵，∴‎ ‎（2）解：取，，，同时取，，‎ ‎ 此时，∴△ABC∽△且 ‎（3）解：不存在这样的△ABC和△，理由如下：‎ ‎ 若，则 ‎ ∴‎ ‎ ∴，而故不存在这样的△ABC和△，使得