2012年玉林市、防城港中考数学试卷 9页

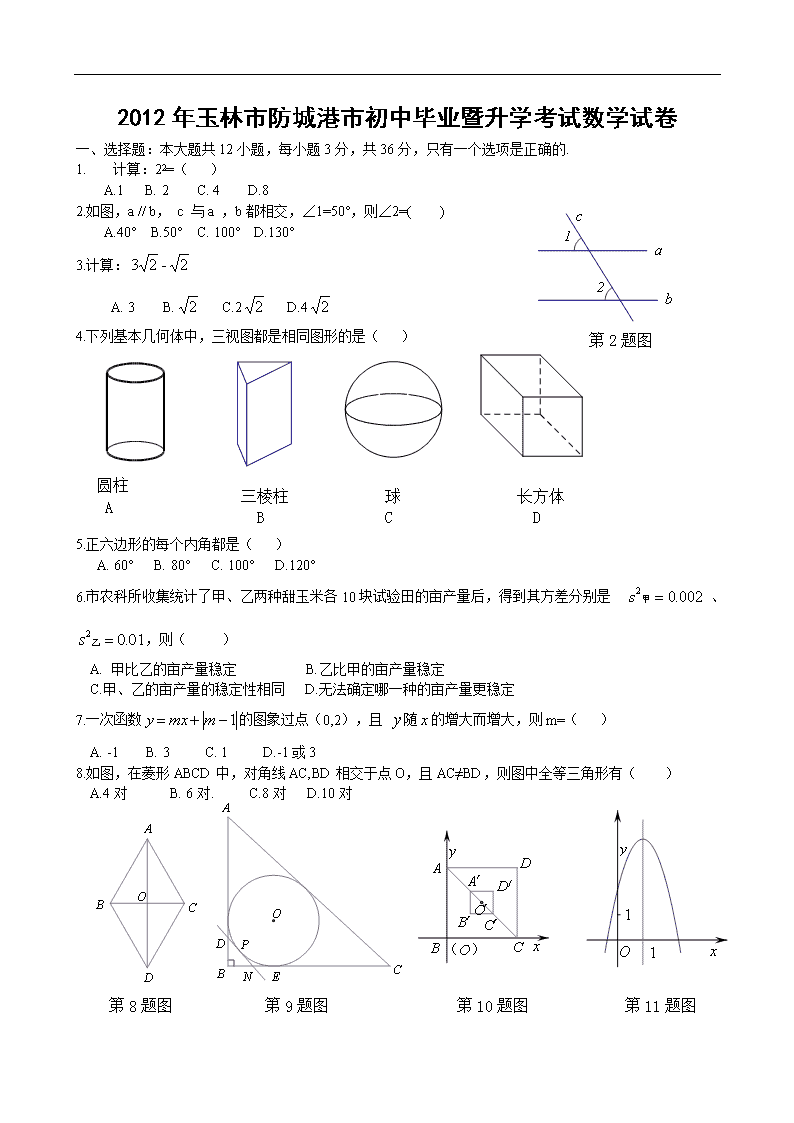
‎2012年玉林市防城港市初中毕业暨升学考试数学试卷 一、选择题：本大题共12小题，每小题3分，共36分，只有一个选项是正确的.‎ ‎1.       计算：22=（ ）‎ A.1 B. 2 C. 4 D.8‎ ‎2.如图，a // b， c 与a ，b都相交，∠1=50°，则∠2=( )‎ A.40° B.50° C. 100° D.130°‎ ‎3.计算：‎ A. 3 B. C.2 D.4‎ 第2题图 ‎4.下列基本几何体中，三视图都是相同图形的是（ ）‎ 长方体 D 球 C 三棱柱 B 圆柱 A ‎5.正六边形的每个内角都是（ ）‎ A. 60° B. 80° C. 100° D.120°‎ ‎6.市农科所收集统计了甲、乙两种甜玉米各10块试验田的亩产量后，得到其方差分别是 、，则（ ）‎ A. 甲比乙的亩产量稳定 B.乙比甲的亩产量稳定 C.甲、乙的亩产量的稳定性相同 D.无法确定哪一种的亩产量更稳定 ‎7.一次函数的图象过点（0,2），且 随的增大而增大，则m=（ ）‎ A. -1 B. 3 C. 1 D.-1或3‎ ‎8.如图，在菱形ABCD中，对角线AC,BD相交于点O，且AC≠BD，则图中全等三角形有（ ）‎ A.4对 B. 6对. C.8对 D.10对 第11题图 第10题图 第9题图 第8题图 ‎9.如图，Rt△ABC的内切圆⊙O与两直角边AB，BC分别相切与点D、E,过劣弧DE（不包括端点D，E）上任一点P作⊙O的切线MN与AB，BC分别交于点M，N，若⊙O的半径为r，则Rt△MBN的周长为（ ）‎ A. r B. r C.2r D. r ‎10.如图，正方形ABCD的两边BC，AB分别在平面直角坐标系的轴、轴的正半轴上，正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形，已知AC=，若点A′的坐标为（1,2），则正方形A′B′C′D′与正方形ABCD的相似比是（ ）‎ A. B. C. D. ‎ ‎11.二次函数（≠0）的图像如图所示，其对称轴为=1，有如下结论：‎ ‎① ＜1 ②2+=0 ③＜4 ④若方程的两个根为，，则+=2.‎ 则结论正确的是（ ）‎ A.      ①② B. ①③ C. ②④ D. ③④‎ ‎12.一个盒子里有完全相同的三个小球，球上分别标有数字-1、1、2.随机摸出一个小球（不放回）其数字记为P ，再随机摸出另一个小球其数字记为q ，则满足关于的方程 有实数根的概率是（ ）‎ A. B. C. D. 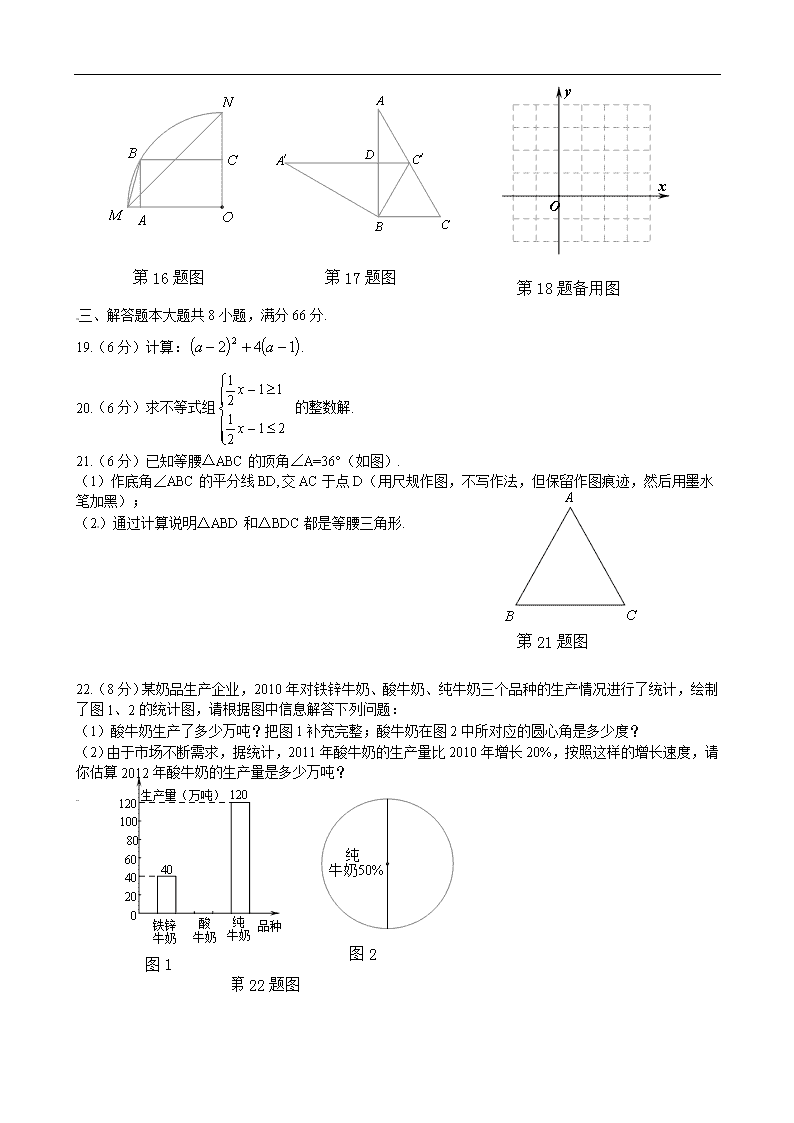‎ 二、填空题：本大题共6小题，每小题3分，共18分，‎ ‎13.既不是正数也不是负数的数是 .‎ ‎14.某种原子直径为1.2×10-2纳米，把这个数化为小数是 纳米.‎ ‎15.在平面直角坐标系中，一青蛙从点A(-1,0)处向右跳2个单位长度，再向上跳2个单位长度到点A′处，则点A′的坐标为 .‎ ‎16.如图，矩形OABC内接于扇形MON，当CN=CO时，∠NMB的度数是 .‎ ‎17.如图，两块相同的三角板完全重合在一起，∠A=30°，AC=10，把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置，点C′在AC上，A′C ′与AB相交于点D，则C′D= .‎ ‎18.二次函数的图像与轴围成的封闭区域内（包括边界），横、纵坐标都是整数的点有 个（提示：必要时可利用下面的备用图画出图像来分析）.‎ 第18题备用图 第17题图 第16题图 ‎ ‎ 三、解答题本大题共8小题，满分66分.‎ ‎19.（6分）计算：.‎ ‎20.（6分）求不等式组 的整数解.‎ ‎21.（6分）已知等腰△ABC的顶角∠A=36°（如图）.‎ ‎（1）作底角∠ABC的平分线BD,交AC于点D（用尺规作图，不写作法，但保留作图痕迹，然后用墨水笔加黑）；‎ ‎（2）通过计算说明△ABD和△BDC都是等腰三角形.‎ 第21题图 ‎22.（8分）某奶品生产企业，2010年对铁锌牛奶、酸牛奶、纯牛奶三个品种的生产情况进行了统计，绘制了图1、2的统计图，请根据图中信息解答下列问题：‎ ‎（1）酸牛奶生产了多少万吨？把图1补充完整；酸牛奶在图2中所对应的圆心角是多少度？‎ ‎（2）由于市场不断需求，据统计，2011年酸牛奶的生产量比2010年增长20%，按照这样的增长速度，请你估算2012年酸牛奶的生产量是多少万吨？‎ 图2‎ 图1‎ 第22题图 ‎23.（8分）如图，已知点O为Rt△ABC斜边上一点，以点O为圆心，OA长为半径的⊙O与BC相切于点E，与AC相交于点D ,连接AE.‎ ‎(1)求证：AE平分∠CAB;‎ ‎(2)探求图中∠1与∠C的数量关系，并求当AE=EC时tanC的值.‎ 第23题图 ‎24.（10分）一工地计划租用甲、乙两辆车清理淤泥，从运输量来估算：若租两车合运，10天可以完成任务；若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.‎ ‎（1）甲、乙两车单独完成任务分别需要多少天？‎ ‎（2）已知两车合运共需租金65000元，甲车每天的租金比乙车每天的租金多1500元，试问：租甲乙两车、单独租甲车、单独租乙车这三种租车方案中，哪一种租金最少？请说明理由.‎ ‎25.（10分）如图，在平面直角坐标系O中，梯形AOBC的边OB在轴的正半轴上，AC//OB,BC⊥OB,过点A的双曲线的一支在第一象限交梯形对角线OC于点D,交边BC于点E.‎ ‎（1）填空：双曲线的另一支在第 象限，的取值范围是 ；‎ ‎（2）若点C的坐标为（2,2），当点E 在什么位置时，阴影部分面积S最小？‎ ‎（3）若，S△OAC=2 ，求双曲线的解析式.‎ 第25题图 ‎26.（12分）如图，在平面直角坐标系O中，矩形AOCD的顶点A的坐标是（0,4），现有两动点P、Q，点P从点O出发沿线段OC（不包括端点O，C）以每秒2个单位长度的速度，匀速向点C运动，点Q 从点C出发沿线段CD（不包括端点C，D）以每秒1个单位长度的速度匀速向点D运动.点P，Q同时出发，同时停止，设运动时间为t秒，当t=2秒时PQ=.‎ ‎（1）求点D的坐标，并直接写出t的取值范围；‎ ‎（2）连接AQ并延长交轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF，则 ‎△AEF的面积S是否随t的变化而变化？若变化，求出S与t的函数关系式；若不变化，求出S的值.‎ ‎（3）在（2）的条件下，t为何值时，四边形APQF是梯形？‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎.‎ ‎ ‎ ‎ ‎ 第26题图 ‎2012年玉林市防城港市初中毕业暨升学考试参考答案 数 学 ‎1.C；2.B；3.C；4.C；5.D；6.A；7.B；8.C；9.C；10B；11.C；12.A；‎ ‎13.0；‎14.0.012‎；15.（1，2）‎ ‎16.30°；17. ；18.7；‎ ‎19.解：原式=a2+4‎-4a+‎4a-4‎ ‎=a2‎ ‎20. 由得：x≥4，‎ 由得：x≤6，‎ 不等式组的解集为：4≤x≤6，‎ 故整数解是：x=4，5，6．‎ ‎21. 解：（1）如图所示：‎ BD即为所求；‎ ‎（2）∵∠A=36°，‎ ‎∴∠ABC=∠C=（180°-36°）÷2=72°，‎ ‎∵BD平分∠ABC，‎ ‎∴∠ABD=∠DBC=72°÷2=36°，‎ ‎∴∠CDB=180°-36°-72°=72°，‎ ‎∵∠A=∠ABD=36°，∠C=∠CDB=72°，‎ ‎∴AD=DB，BD=BC，‎ ‎∴△ABD和△BDC都是等腰三角形．‎ ‎22．‎ 解：（1）牛奶总产量=120÷50%=240吨，‎ 酸牛奶产量=240-40-120=80吨，‎ 酸牛奶在图2所对应的圆心角度数为×360°=120°．‎ ‎（2）2012年酸牛奶的生产量为80×（1+20%）2=115.2吨．‎ 答：2012年酸牛奶的生产量是115.2万吨．‎ ‎23. 证明：连接OE， ∵⊙O与BC相切于点E， ∴OE⊥BC， ∵AB⊥BC， ∴AB∥OE， ∴∠2=∠AEO， ∵OA=OE， ∴∠1=∠AEO， ∴∠1=∠2，即AE平分∠CAB； ‎ ‎（2）解：2∠1+∠C=90°，tanC=‎ ‎∵∠EOC是△AOE的外角， ∴∠1+∠AEO=∠EOC， ∵∠1=∠AEO，∠OEC=90°， ∴2∠1+∠C=90°， 当AE=CE时，∠1=∠C， ∵2∠1+∠C=90° ∴3∠C=90°，∠C=30° ∴tanC=tan30°=‎ ‎24. 设甲车单独完成任务需要x天，乙单独完成需要y天，‎ 由题意可得：；‎ 解得：x=15；y=30‎ 即甲车单独完成需要15天，乙车单独完成需要30天；‎ ‎（2）设甲车租金为a，乙车租金为y，‎ 则根据两车合运共需租金65000元，甲车每天的租金比乙车每天的租金多1500元可得：‎ ‎10a‎+10b=65000；a-b=1500，‎ 解得：a=4000；b=2500，‎ ‎①租甲乙两车需要费用为：65000元；‎ ‎②单独租甲车的费用为：15×4000=60000元；‎ ‎③单独租乙车需要的费用为：30×2500=75000元；‎ 综上可得，单独租甲车租金最少．‎ ‎25. （1）三，k＞0，‎ ‎（2）∵梯形AOBC的边OB在x轴的正半轴上，AC∥OB，BC⊥OB， 而点C的坐标标为（2，2）， ∴A点的纵坐标为2，E点的横坐标为2，B点坐标为（2，0）， 把y=2代入y=得x=；把x=2代入y=得y=‎ ‎∴A点的坐标为（，2），E点的坐标为（2，），‎ ‎∴S阴影部分=S△ACE+S△OBE=×（2-）×（2-）+×2×=k2-k+2=（k-2）2+1.5‎ 当k-2=0，即k=2时，S阴影部分最小，最小值为1.5；‎ ‎∴E点的坐标为（2，1），即E点为BC的中点， ∴当点E在BC的中点时，阴影部分的面积S最小； （3）设D点坐标为（a，），‎ ‎∵OD：OC=1：2，‎ ‎∴OD=DC，即D点为OC的中点， ∴C点坐标为（‎2a，），‎ ‎∴A点的纵坐标为，‎ 把y=代入y=得x=，‎ ‎∴A点坐标为（，），‎ ‎∵S△OAC=2，‎ ‎∴×（‎2a-）×=2，‎ ‎∴k=。‎ ‎∴双曲线的解析式y＝。‎ ‎26. 解：（1）由题意可知，当t=2（秒）时，OP=4，CQ=2， 在Rt△PCQ中，由勾股定理得：PC===4，‎ ‎∴OC=OP+PC=4+4=8，[‎ 又∵矩形AOCD，A（0，4），∴D（8，4）．‎ 点P到达终点所需时间为8÷2=4秒，点Q到达终点所需时间为4÷1=4秒，由题意可知，t的取值范围为：0＜t＜4。‎ ‎（2）结论：△AEF的面积S不变化．‎ ‎∵AOCD是矩形，∴AD∥OE，∴△AQD∽△EQC，‎ ‎∴=，即=，解得CE=。‎ 由翻折变换的性质可知：DF=DQ=4-t，则CF=CD+DF=8-t．‎ S=S梯形AOCF+S△FCE-S△AOE ‎=（OA+CF）•OC+CF•CE-OA•OE ‎=[4+（8-t）]×8+（8-t）•-×4×（8+）‎ 化简得：S=32为定值．‎ 所以△AEF的面积S不变化，S=32．‎ ‎（3）若四边形APQF是梯形，因为AP与CF不平行，所以只有PQ∥AF．‎ 由PQ∥AF可得：△CPQ∽△DAF，‎ ‎∴CP：AD=CQ：DF，即8-2t：8= t：4-t，化简得t2-12t+16=0，‎ 解得：t1=6+2，t2=，‎ 由（1）可知，0＜t＜4，∴t1=6+2不符合题意，舍去．‎ ‎∴当t=（6-2）秒时，四边形APQF是梯形．‎