中考数学试题分类汇编共专题三角形等腰三角形等边三角形全等尺规作图 29页

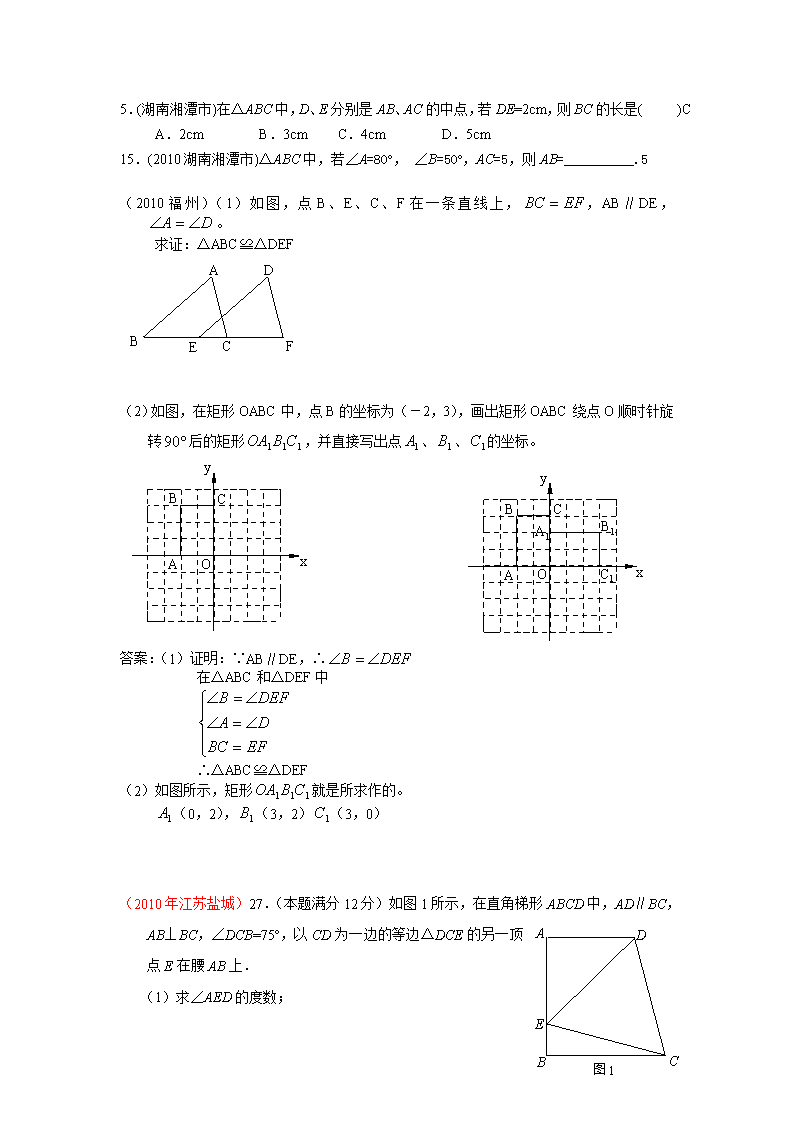
‎5．(湖南湘潭市)在△ABC中，D、E分别是AB、AC的中点，若DE=‎2cm，则BC的长是( )C ‎ A．‎2cm B．‎3cm 　 C．‎4cm D．‎‎5cm ‎15．(2010湖南湘潭市)△ABC中，若∠A=80o， ∠B=50o，AC=5，则AB= .5‎ ‎（2010福州）（1）如图，点B、E、C、F在一条直线上，，AB∥DE，。‎ ‎ 求证：△ABC≌△DEF A B E C F D O y x C A B ‎（2）如图，在矩形OABC中，点B的坐标为（－2，3），画出矩形OABC绕点O顺时针旋转后的矩形，并直接写出点、、的坐标。‎ O y x C A B A1‎ B1‎ C1‎ 答案：（1）证明：∵AB∥DE，∴‎ ‎ 在△ABC和△DEF中 ‎ ‎ ‎ ∴△ABC≌△DEF ‎（2）如图所示，矩形就是所求作的。‎ ‎ （0，2），（3，2）（3，0）‎ ‎（2010年江苏盐城）A B C D E 图1‎ 27．（本题满分12分）如图1所示，在直角梯形ABCD中，AD∥BC，AB⊥BC，∠DCB=75º，以CD为一边的等边△DCE的另一顶点E在腰AB上．‎ ‎（1）求∠AED的度数；‎ ‎（2）求证：AB=BC；‎ ‎（3）如图2所示，若F为线段CD上一点，∠FBC=30º．‎ 求 的值． ‎ A B C D E F 图2‎ ‎(1)∵∠BCD=75º，AD∥BC ∴∠ADC=105º …………………………………（1分）‎ ‎ 由等边△DCE可知：∠CDE =60º，故∠ADE =45º 由AB⊥BC，AD∥BC可得：∠DAB=90º ， ∴∠AED=45º…………………（3分）‎ ‎ (2)方法一：由(1)知：∠AED=45º，∴AD=AE，故点A在线段DE的垂直平分线上．‎ 由△DCE是等边三角形得：CD=CE，故点C也在线段DE的垂直平分线上．‎ ‎∴AC就是线段DE的垂直平分线，即AC⊥DE…………………（5分）‎ 连接AC，∵∠AED =45º，∴∠BAC=45º，又AB⊥BC ∴BA=BC．…………（7分）‎ D A 方法二：过D点作DF⊥BC，交BC于点 ………………（4分）‎ 可证得：△DFC≌△CBE 则DF=BC……………………（6分）‎ 从而：AB=CB ………………………………………………（7分）‎ E ‎（3）∵∠FBC=30º，∴∠ABF=60º 连接AF，BF、AD的延长线相交于点G，‎ 图1‎ F C B ‎∵∠FBC=30º，∠DCB=75º，∴∠BFC=75º，故BC=BF G D A 由(2)知：BA=BC，故BA=BF，∵∠ABF=60º，∴AB=BF=FA，‎ 又∵AD∥BC，AB⊥BC，∴∠FAG=∠G=30º ‎∴FG =FA= FB ……………………………（10分）‎ F ‎∵∠G=∠FBC=30º，∠DFG=∠CFB，FB=FG E ‎∴△BCF≌△GDF ………………………（11分）‎ C 图2‎ B ‎∴DF=CF，即点F是线段CD的中点．‎ ‎∴=1………………………………………（12分）‎ ‎(注:如其它方法仿此得分)‎ ‎（2010年浙江省绍兴市）15.做如下操作：在等腰三角形ABC中,AB= AC,AD平分∠BAC,‎ 交BC于点D.将△ABD作关于直线AD的轴对称变换,所得的 像与△ACD重合.‎ 第15题图 对于下列结论:①在同一个三角形中,等角对等边;②在同一个三角形中,等边对等角;③等腰三角形的顶角平分线、底边上的中线 和高互相重合.‎ 由上述操作可得出的是 ②③ (将正确结论的序号都填上)‎ ‎2010丽水 2.　如图，D，E分别是△ABC的边AC和BC的中点，已知DE=2，则AB=‎ A．1 B．‎2 ‎ C．3 D．4‎ 答案： D ‎ (2010年 丹东市)15．已知△ABC是边长为1的等腰直角三角形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，第n个等腰直角三角形的斜边长是 ．答案：‎ 第15题图 ‎(2010年 丹东市)25．如图， 已知等边三角形ABC中，点D，E，F分别为边AB，AC，BC的中点，M为直线BC上一动点，△DMN为等边三角形（点M的位置改变时， △DMN也随之整体移动） ．‎ ‎ （1）如图①，当点M在点B左侧时，请你判断EN与MF有怎样的数量关系？点F是否在直线NE上？都请直接写出结论，不必证明或说明理由；‎ ‎ （2）如图②，当点M在BC上时，其它条件不变，（1）的结论中EN与MF的数量关系是否仍然成立?若成立，请利用图②证明；若不成立，请说明理由；‎ ‎（3）若点M在点C右侧时，请你在图③中画出相应的图形，并判断（1）的结论中EN与MF的数量关系是否仍然成立?若成立?请直接写出结论，不必证明或说明理由． ‎ 图①‎ 图②‎ 图③‎ 第25题图 A ‎·‎ B C D E F ‎·‎ ‎·‎ ‎·‎ 答案：（1）判断：EN与MF相等 （或EN=MF），点F在直线NE上， 3分 ‎（说明：答对一个给2分）‎ ‎（2）成立． 4分 证明：‎ 法一：连结DE，DF． 5分 ‎∵△ABC是等边三角形， ∴AB=AC=BC．‎ 又∵D，E，F是三边的中点， ‎ ‎∴DE，DF，EF为三角形的中位线．∴DE=DF=EF，∠FDE=60°．‎ 又∠MDF+∠FDN=60°， ∠NDE+∠FDN=60°， ‎ ‎∴∠MDF=∠NDE． 7分 在△DMF和△DNE中，DF=DE，DM=DN， ∠MDF=∠NDE，‎ ‎∴△DMF≌△DNE． 8分 N C A B F M D E N C A B F M D E ‎∴MF=NE． 　 9分 法二：‎ 延长EN，则EN过点F． 5分 ‎∵△ABC是等边三角形， ∴AB=AC=BC．‎ 又∵D，E，F是三边的中点， ∴EF=DF=BF． ‎ ‎ ∵∠BDM+∠MDF=60°， ∠FDN+∠MDF=60°，‎ ‎∴∠BDM=∠FDN． 7分 又∵DM=DN， ∠ABM=∠DFN=60°，‎ ‎∴△DBM≌△DFN． 8分 ‎∴BM=FN．‎ ‎∵BF=EF， ∴MF=EN． 9分 法三：‎ 连结DF，NF． 5分 ‎∵△ABC是等边三角形， ‎ ‎∴AC=BC=AC．‎ 又∵D，E，F是三边的中点， ‎ ‎∴DF为三角形的中位线，∴DF=AC=AB=DB． ‎ 又∠BDM+∠MDF=60°， ∠NDF+∠MDF=60°， ‎ ‎∴∠BDM=∠FDN． 7分 在△DBM和△DFN中，DF=DB，‎ DM=DN， ∠BDM=∠NDF，∴△DBM≌△DFN． ‎ ‎∴∠B=∠DFN=60°． 8分 又∵△DEF是△ABC各边中点所构成的三角形，‎ ‎∴∠DFE=60°．‎ ‎∴可得点N在EF上，‎ ‎∴MF=EN． 9分 ‎（3）画出图形（连出线段NE）， 11分 MF与EN相等的结论仍然成立（或MF=NE成立）． 12分 ‎(2010年 威海市)2．如图，在△ABC中，∠C＝90°．若BD∥AE，∠DBC＝20°，则∠CAE的度数是（ ）答案：C A B C D E A．40° ‎ B．60° ‎ C．70° ‎ D．80° ‎ ‎(2010年 威海市)A D B E 9．如图，在△ABC中，D，E分别是边AC，AB的中点， ‎ 连接BD．若BD平分∠ABC，则下列结论错误的是 （ ）答案：C A．BC＝2BE ‎ B．∠A＝∠EDA ‎ C C．BC＝2AD ‎ D．BD⊥AC ‎ ‎（2010哈尔滨）１。如图，AB、AC为⊙O的弦，连接CO、BO并延长分别交弦AB、AC于点E、F，∠B＝∠C．求证：CE＝BF．‎ ‎（2010珠海）２。如图，在梯形ABCD中，AB∥CD ‎（1）用尺规作图方法，作∠DAB的角平分线AF（只保留作图痕迹，不写作法和证明）‎ ‎（2）若AF交CD边于点E，判断△ADE的形状（只写结果）‎ 解：(1)所以射线AF即为所求 ‎(2)△ADE是等腰三角形.‎ ‎（2010珠海）３．如图，△ABC内接于⊙O，AB＝6,AC＝4,D是AB边上一点，P是优弧BAC的中点，连结PA、PB、PC、PD.‎ ‎(1)当BD的长度为多少时，△PAD是以AD为底边的等腰三角形？并证明；‎ ‎（2）若cos∠PCB=，求PA的长.‎ 解：（1）当BD＝AC＝4时，△PAD是以AD为底边的等腰三角形 ‎∵P是优弧BAC的中点 ∴弧PB＝弧PC ‎∴PB＝PC ‎∵BD＝AC＝4 ∠PBD=∠PCA ‎∴△PBD≌△PCA ‎∴PA=PD 即△PAD是以AD为底边的等腰三角形 ‎（2）由（1）可知，当BD＝4时，PD＝PA，AD＝AB-BD＝6-4＝2‎ 过点P作PE⊥AD于E，则AE＝AD=1‎ ‎∵∠PCB=∠PAD ‎∴cos∠PAD=cos∠PCB=‎ ‎∴PA=‎ ‎（2010红河自治州）11. 如图3，D、E分别是AB、AC上的点，若∠A=70°，∠B=60°，‎ ‎ DE//BC.则∠AED的度数是 50°.‎ ‎（2010年镇江市）20．推理证明（本小题满分6分）‎ ‎ 如图，在△ABC和△ADE中，点E在BC边上，∠BAC=∠DAE，∠B=∠D，AB=AD.‎ ‎ （1）求证：△ABC≌△ADE；‎ ‎ （2）如果∠AEC=75°，将△ADE绕着点A旋转一个锐角后与△ABC重合，求这个旋转角的大小.‎ ‎（1）∵∠BAC=∠DAE，AB=AD，∠B=∠D，‎ ‎∴△ABD≌△ADE.（3分）‎ ‎ （2）∵△ABC≌△ADE，‎ ‎∴AC与AE是一组对应边，‎ ‎∴∠CAE的旋转角，（4分）‎ ‎∵AE=AC，∠AEC=75°，‎ ‎∴∠ACE=∠AEC=75°， （5分）‎ ‎∴∠CAE=180°—75°—75°=30°. （6分）‎ ‎（玉溪市2010）22. 平面内的两条直线有相交和平行两种位置关系.‎ ‎（1）AB平行于CD．如图a，点P在AB、CD外部时，由AB∥CD，有∠B=∠BOD，又因∠BOD是△POD的外角，故∠BOD=∠BPD +∠D，得∠BPD=∠B-∠D．如图b，将点P移到AB、CD内部，以上结论是否成立？，若不成立，则∠BPD、∠B、∠D 之间有何数量关系？请证明你的结论；‎ 图a O 图b ‎（2）在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，‎ 如图c，则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系？（不需证明）；‎ ‎（3）根据（2）的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数．‎ 图c 图d G O 解：（1）不成立，结论是∠BPD=∠B+∠D.‎ 延长BP交CD于点E,‎ ‎ ∵AB∥CD. ∴∠B=∠BED.‎ 又∠BPD=∠BED+∠D，‎ ‎∴∠BPD=∠B+∠D. …………4分 ‎（2）结论： ∠BPD=∠BQD+∠B+∠D. …………7分 ‎（3）由（2）的结论得：∠AGB=∠A+∠B+∠E.‎ ‎ 又∵∠AGB=∠CGF.‎ ‎ ∠CGF+∠C+∠D+∠F=360°‎ ‎∴∠A+∠B+∠C+∠D∠E+∠F=360°. …………11分 ‎（桂林2010）26．（本题满分12分）如图，过A（8，0）、B（0，）两点的直线与直线交于点C．平行于轴的直线从原点O出发，以每秒1个单位长度的速度沿轴向右平移，到C点时停止；分别交线段BC、OC于点D、E，以DE为边向左侧作等边△DEF，设△DEF与△BCO重叠部分的面积为S（平方单位），直线的运动时间为t（秒）．‎ ‎（1）直接写出C点坐标和t的取值范围； ‎ ‎（2）求S与t的函数关系式；‎ ‎（3）设直线与轴交于点P，是否存在这样的点P，使得以P、O、F为顶点的三角形为等腰三角形，若存在，请直接写出点P的坐标；若不存在，请说明理由．‎ ‎26．(本题12 分)解（1）C（4，） ……………………………2分 的取值范围是：0≤≤4 ……………………………… 3分 ‎（2）∵D点的坐标是（，），E的坐标是（，）‎ ‎∴DE=-= ……………………4分 ‎∴等边△DEF的DE边上的高为： ‎ ‎∴当点F在BO边上时：=，∴=3 ……………………5分 ① 当0≤<3时，重叠部分为等腰梯形，可求梯形上底为：- …7分 S=‎ ‎=‎ ‎= ………………………………8分 ② 当3≤≤4时，重叠部分为等边三角形 S= ………………… 9分 ‎= ……………………10分 ‎（3）存在，P（，0） ……………………12分 说明：∵FO≥，FP≥，OP≤4‎ ‎∴以P，O，F以顶点的等腰三角形，腰只有可能是FO，FP,‎ 若FO=FP时，=2（12-3），=，∴P（，0） ‎ ‎（2010年无锡）7．下列性质中，等腰三角形具有而直角三角形不一定具有的是 （ ▲ ）‎ A．两边之和大于第三边 B．有一个角的平分线垂直于这个角的对边 C．有两个锐角的和等于90° D．内角和等于180°‎ 答案 B ‎ ‎（2010年无锡）16．如图,△ABC中,DE垂直平分AC交AB于E,∠A=30°,∠ACB=80°,则∠BCE= ▲ °．‎ 答案 50 ‎ ‎（第16题）‎ ‎ 2010年无锡）26．（本题满分10分）‎ ‎（1）如图1，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点,P是BC延长线上一点，N是∠DCP的平分线上一点．若∠AMN=90°，求证：AM=MN．‎ 下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明．‎ 证明：在边AB上截取AE=MC，连ME．正方形ABCD中，∠B=∠BCD=90°，‎ AB=BC．∴∠NMC=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠MAB 图1‎ ‎=∠MAE．本试卷由无锡市天一实验学校金杨建录制 QQ：623300747．转载请注明！‎ ‎（下面请你完成余下的证明过程）‎ 图2‎ ‎（2）若将(1)中的“正方形ABCD”改为“正三角形ABC”（如图2）,N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．‎ 本试卷由无锡市天一实验学校金杨建录制 QQ：623300747．转载请注明！‎ ‎（3）若将（1）中的“正方形ABCD”改为“正边形ABCD…X ‎”，请你作出猜想：当∠AMN ‎= °时，结论AM=MN仍然成立．（直接写出答案，不需要证明）‎ 答案解：‎ ‎（1）∵AE=MC,∴BE=BM, ∴∠BEM=∠EMB=45°, ∴∠AEM=1355°, ‎ ‎ ∵CN平分∠DCP，∴∠PCN=45°，∴∠AEM=∠MCN=135°‎ ‎ 在△AEM和△MCN中：∵∴△AEM≌△MCN，∴AM=MN ‎ （2）仍然成立．‎ ‎ 在边AB上截取AE=MC，连接ME ‎ ∵△ABC是等边三角形，‎ ‎ ∴AB=BC，∠B=∠ACB=60°，‎ ‎ ∴∠ACP=120°．‎ ‎ ∵AE=MC，∴BE=BM ‎ ∴∠BEM=∠EMB=60°‎ ‎ ∴∠AEM=120°．‎ ‎ ∵CN平分∠ACP，∴∠PCN=60°，‎ ‎ ∴∠AEM=∠MCN=120°‎ ‎ ∵∠CMN=180°—∠AMN—∠AMB=180°—∠B—∠AMB=∠BAM ‎ ∴△AEM≌△MCN，∴AM=MN ‎ （3）‎ ‎ ‎ ‎（2010宁波市）C A B D E 第10题 10．如图，在△ABC中，AB＝AC，∠A＝36°，BD、CE分别是△ABC、△BCD的角平分线，则图中的等腰三角形有 A ‎ A．5个 B．4个 C．3个 D．2个 ‎18．（2010年金华）(本题6分)‎ 如图，在△ABC中，D是BC边上的点（不与B，C重合），F，E分别是AD及其延长线上的点，CF∥BE. 请你添加一个条件，使△BDE≌△CDF (不再添加其它线段，不再标注或使用其他字母)，并给出证明．‎ ‎（1）你添加的条件是： ▲ ；‎ ‎（2）证明： ‎ A C B D F E ‎(第18题图)‎ ‎ 解：（1）(或点D是线段BC的中点)，，中 任选一个即可﹒………………………………2分 ‎（2）以为例进行证明：‎ ‎∵CF∥BE， ‎ ‎∴∠FCD﹦∠EBD．‎ ‎ 又∵，∠FDC﹦∠EDB，‎ ‎ ∴△BDE≌△CDF．…………………4分 A C B D F E ‎．··．‎ ‎5．（2010年长沙）下列每一组数据中的三个数值分别为三角形的三边长，不能构成直角三角形的是 C A．3、4、5 B．6、8、‎10 ‎ C．、2、 D．5、12、13‎ ‎22．（2010年长沙）在正方形ABCD中，AC为对角线，E为AC上一点，连接EB、ED．‎ ‎（1）求证：△BEC≌△DEC；‎ ‎（2）延长BE交AD于F，当∠BED=120°时，求∠EFD的度数．‎ 第22题图 A F D E B C 答案：（1）证明：∵四边形ABCD是正方形 ‎∴BC＝CD，∠ECB＝∠ECD＝45°‎ 又EC＝EC …………………………2分 ‎∴△ABE≌△ADE ……………………3分 ‎（2）∵△ABE≌△ADE ‎∴∠BEC＝∠DEC＝∠BED …………4分 ‎ ‎∵∠BED＝120°∴∠BEC＝60°＝∠AEF ……………5分 ‎∴∠EFD＝60°+45°＝105° …………………………6分 ‎ (2010湖北省荆门市)6．给出以下判断：(1)线段的中点是线段的重心 ‎ (2)三角形的三条中线交于一点，这一点就是三角形的重心 ‎ (3)平行四边形的重心是它的两条对角线的交点 ‎ (4)三角形的重心是它的中线的一个三等分点 那么以上判断中正确的有( )‎ ‎(A)一个 (B)两个 (C)三个 (D)四个 答案D 第11题 ‎11. （2010年郴州市）如图3，一个直角三角形纸片，剪去直角后，得到一个四边形，则　 度．‎ 答案：270‎ ‎3．（2010年济宁市)若一个三角形三个内角度数的比为2︰3︰4，那么这个三角形是 A. 直角三角形 B. 锐角三角形 C. 钝角三角形 D. 等边三角形 ‎ 答案：B 北京3. 如图，在△ABC中，点D、E分AB、AC边上，DE//BC，若AD：AB=3：4，‎ ‎ AE=6，则AC等于 (A) 3 (B) 4 (C) 6 (D) 8。‎ 北京15. 已知：如图，点A、B、C、D在同一条直线上，EA^AD，FD^AD，AE=DF，‎ ‎ AB=DC。求证：ÐACE=ÐDBF。‎ 毕节18．三角形的每条边的长都是方程的根，则三角形的周长是 ．18． 6或10或12‎ ‎19．(10重庆潼南县)画一个等腰△ABC，使底边长BC=a，底边上的高为h（要求：用尺规作图，保留作图痕迹，写出已知，求作，不写作法和证明）．‎ 已知：‎ 求作：‎ 已知：线段a、h ‎ 求作：一个等腰△ABC使底边BC=a，底边BC上的高为h。-------------1分 画图（保留作图痕迹图略）--------------------------6分 ‎24．全等、四边形、勾股定理(10重庆潼南县)如图,四边形ABCD是边长为2的正方形，点G是BC延长线上一点，连结AG，点E、F分别在AG上，连接BE、DF，∠1=∠2，∠3=∠4．‎ ‎（1）证明：△ABE≌△DAF；‎ ‎（2）若∠AGB=30°，求EF的长．‎ 解：（1）∵四边形ABCD是正方形，∴AB=AD。‎ 在△ABE和△DAF中，‎ ‎∴△ABE≌△DAF。‎ ‎（2）∵四边形ABCD是正方形，∴∠1+∠4=900。‎ ‎∵∠3=∠4，∴∠1+∠3=900。∴∠AFD=900。‎ 在正方形ABCD中，AD∥BC，∴∠1=∠AGB=300。‎ 在Rt△ADF中，∠AFD=900，AD=2，∴AF=，DF =1。‎ 由(1)得△ABE≌△ADF。∴AE=DF=1。∴EF=AF-AE=。‎ ‎1、如图，已知点在线段上，，请在下列四个等式中，‎ C E B F D A ‎①AB＝DE，②∠ACB＝∠F，③∠A＝∠D，④AC＝DF．选出两个作为条件，推出．并予以证明．（写出一种即可）‎ 已知：　 　　 　，　 　　 　．‎ 求证：．‎ 证明：‎ 答案：C E B F D A 解：已知：①④（或②③、或②④）‎ 证明：若选①④‎ ‎∵‎ ‎∴．‎ 在△ABC和△DEF中 AB＝DE，BC＝EF，AC＝DF．‎ ‎∴．‎ ‎（选择②③、或②④评分标准类似，证明略）‎ ‎（2010年天津市）（13）如图，已知，，‎ 第（13）题 A C D B E F 点A、D、B、F在一 条直线上，要使△≌△，还需添加 一个条件，这个条件可以是 ‎ ‎（答案不惟一，也可以是或） ． ‎ ‎（2010山西9．现有四根木棒，长度分别为‎4cm，‎6cm，‎8cm，‎10cm.从中任取一根木棒，能组成三角形的个数为（）C A．1个 B．2个 C．3个 D．4个 ‎（2010山西25．（本题10分）如图1，已知正方形ABCD的边CD在正方形DEFG的边DE上，连接AE、GC．‎ ‎（1）试猜想AE与GC有怎样的位置关系，并证明你的结论．‎ ‎（2）将正方形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图2，连接AE和CG。你认为（1‎ ‎）中的结论是否还成立？若成立，给出证明；若不成立，请说明理由．‎ A B G D E ‎（第25题）‎ F C A B G D E F C ‎（图1）‎ ‎（图2）‎ ‎1.（2010宁德）如图所示，如果将矩形纸沿虚线①对折后，沿虚线②剪开，剪出一个 直角三角形，展开后得到一个等腰三角形.则展开后三角形的周长是（ ）.B ‎①‎ ‎②‎ ‎3‎ ‎4‎ ‎10‎ A．2＋ B．2＋‎2‎ C．12 D．18‎ A B C E F 第14题图 ‎2.（2010宁德）如图，在△ABC中，点E、F分别为AB、AC的中点．‎ 若EF的长为2，则BC的长为___________.4‎ ‎3.（2010宁德）（本题满分8分）如图，已知AD是△ABC 的角平分线，在不添加任何辅助线的前提下，要使△AED≌△AFD，需添加一个条件是：_______________，并给予证明.‎ B D C A E F 解法一：添加条件：AE＝AF，………………3分 ‎ 证明：在△AED与△AFD中，‎ ‎∵AE＝AF，∠EAD＝∠FAD，AD＝AD，………………6分 ‎∴△AED≌△AFD（SAS）. ………………8分 解法二：添加条件：∠EDA＝∠FDA，………………3分 证明：在△AED与△AFD中，‎ ‎ ∵∠EAD＝∠FAD，AD＝AD，∠EDA＝∠FDA，………………6分 ‎ ∴△AED≌△AFD（ASA）. ………………8分 ‎4.（2010黄冈）如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA＝CQ时，连PQ交AC边于D，则DE的长为（　　　）B A．　　B．　　C．　　D．不能确定 ‎　　　　　第15题图 A B C D E F 第11题图图 ‎1．(2010昆明)如图，在△ABC中，点D、E、F分别是AB、BC、CA的中点，‎ 若△ABC的周长为10 cm，则△DEF的周长是　　　　 cm．‎ 答案：5‎ D A B C 第6题图 ‎2．（2010山东济南）如图，在△ABC中，CD是∠ACB的平分线，∠A = 80°，∠ACB=60°，那么∠BDC=（　　）　‎ ‎ A．80° B．90° ‎ C．100° D．110°‎ 答案：D A B C D P E 第12题图 ‎3．（2010山东济南）如图所示，矩形ABCD中，AB=4，BC=，点E是折线段A－D－C上的一个动点（点E与点A不重合），点P是点A关于BE的对称点．在点E运动的过程中，使△PCB为等腰三角形的点E的位置共有 A．2个 B．3个 C．4个 D．5个 答案：C ‎23．（2010山东济南） ‎ 已知：△ABC是任意三角形．‎ ‎⑴如图1所示，点M、P、N分别是边AB、BC、CA的中点．求证：∠MPN=∠A．‎ ‎⑵如图2所示，点M、N分别在边AB、AC上，且，，点P1、P2是边BC的三等分点，你认为∠MP1N+∠MP2N=∠A是否正确？请说明你的理由．‎ A B C N M P A M N P1‎ C P2‎ B A C M N P1‎ P2‎ P2009‎ ‎……‎ ‎……‎ B 第23题图2‎ 第23题图1‎ 第23题图3‎ ‎⑶如图3所示，点M、N分别在边AB、AC上，且，，点P1、P2、……、P2009是边BC的2010等分点，则∠MP1N+∠MP2N+……+∠MP2009N=____________．‎ ‎（请直接将该小问的答案写在横线上．）‎ 答案：23. ⑴证明：∵点M、P、N分别是AB、BC、CA的中点，‎ A B C M N P1‎ 第23题图 P2‎ ‎1‎ ‎2‎ ‎ ∴线段MP、PN是△ABC的中位线，‎ ‎∴MP∥AN，PN∥AM， 1分 ‎ ∴四边形AMPN是平行四边形， 2分 ‎ ∴∠MPN=∠A. 3分 ‎⑵∠MP1N+∠MP2N=∠A正确. 4分 如图所示，连接MN， 5分 ‎∵，∠A=∠A，‎ ‎∴△AMN∽△ABC，‎ ‎∴∠AMN=∠B，， ‎ ‎∴MN∥BC，MN=BC， 6分 ‎∵点P1、P2是边BC的三等分点，‎ ‎∴MN与BP1平行且相等，MN与P1P2平行且相等，MN与P‎2C平行且相等，‎ ‎∴四边形MBP1N、MP1P2N、MP2CN都是平行四边形，‎ ‎∴MB∥NP1，MP1∥NP2，MP2∥AC，‎ ‎ 7分 ‎∴∠MP1N=∠1，∠MP2N=∠2，∠BMP2=∠A，‎ ‎∴∠MP1N+∠MP2N=∠1+∠2=∠BMP2=∠A.‎ ‎ 8分 ‎⑶∠A. 9分 ‎17．(2010昆明)如图，点B、D、C、F在一条直线上，且BC = FD，AB = EF.‎ F A B C D E ‎（1）请你只添加一个条件（不再加辅助线），使△ABC≌△EFD，你添加的条件是 ；‎ ‎（2）添加了条件后，证明△ABC≌△EFD.‎ 答案：（1）∠B = ∠F　或　AB∥EF　或　AC = ED. ………………2分 ‎ （2）证明：当∠B = ∠F时 ‎ 在△ABC和△EFD中 ‎ ………………5分 ‎ ∴△ABC≌△EFD (SAS) …………………6分 ‎（本题其它证法参照此标准给分）‎ A B C P0‎ P1‎ P2‎ P3‎ 第15题图 ‎1．（2010山东德州）电子跳蚤游戏盘是如图所示的△ABC，AB=AC=BC=6．如果跳蚤开始时在BC边的P0处，BP0=2．跳蚤第一步从P0跳到AC边的P1（第1次落点）处，且CP1= CP0；第二步从P1跳到AB边的P2（第2次落点）处，且AP2= AP1；第三步从P2跳到BC边的P3（第3次落点）处，且BP3= BP2；…；跳蚤按照上述规则一直跳下去，第n次落点为Pn（n为正整数），则点P2009与点P2010之间的距离为_________．‎ ‎2、 （2010四川宜宾）如图，分别过点C、B作△ABC的BC边上的中线AD及其延长线的垂线，垂足分 别为E、F．求证：BF=CE．‎ ‎13（3）题图 ‎3、（2010四川宜宾）‎ 已知：如图，在Rt△ABC中，∠C=90°，过点B作BD∥AC，且BD=2AC，连接AD．‎ ‎21题图 试判断△ABD的形状，并说明理由．‎ ‎4．（2010山东德州）‎ A D B E F C O 第18题图 如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O．‎ ‎(1)求证：AB＝DC；‎ ‎(2)试判断△OEF的形状，并说明理由．‎ 答案：1． 2;‎ ‎2、证明：∵ CE⊥AD于E，BF⊥AD于F，‎ ‎∴∠CED =∠BFD =90°． …………………………………………………l分 又∵AD是BC边上的中线，‎ ‎∴BD =CD． …………………………………………………………………2分 又∵∠BDF=∠CDE， ………………………………………………………3分 ‎∴△BDF≌△CDE． …………………………………………………………4分 故BF=CE． …………………………………………………………5分 ‎3、解：△ABD是等腰三角形．………………………………………………………………l分 在BD上取点E，使BE=AC，连接AE，‎ ‎∵AC∥BD，BE = AC，‎ ‎∴四边形ACBE是平行四边形．………………………………………………… 3分 又∵∠C = 90°‎ ‎∴四边形ACBE是矩形． …………………………………………………………5分 ‎∴AE⊥BD．…………………………………………………………………………6分 又∵BE = AC = BD，……………………………………………………………7分 ‎∴BE = ED．‎ ‎∴AB=AD． ……………………………………………………………………… 8分 故△ABD是等腰三角形．‎ ‎4．证明：（１）∵BE＝CF，‎ ‎∴BE＋EF＝CF＋EF， …………1分 即BF＝CE． …………………2分 又∵∠A＝∠D，∠B＝∠C，‎ ‎∴△ABF≌△DCE（AAS）， ……………………………………4分 ‎∴AB＝DC． ………………………………………5分 ‎（２）△OEF为等腰三角形 …………………………………6分 理由如下：∵△ABF≌△DCE，‎ ‎∴∠AFB=∠DEC．‎ ‎∴OE=OF．‎ ‎∴△OEF为等腰三角形． …………………………………8分 ‎（2010株洲市）8．如图所示的正方形网格中，网格线的交点称为格点．已知、‎ 是两格点，如果也是图中的格点，且使得为等腰三角形，则点的个数是 A．6 B．‎7 ‎C．8 D．9‎ 第8题图 ‎（2010年常州）22.（本小题满分5分）如图，在△ABC中，点D、E分别在边AC、AB上，BD=CE，∠DBC=∠ECB.‎ 求证：AB=AC.‎ A B C D ‎40°‎ ‎120°‎ 图1‎ ‎（2010河北省）2．如图1，在△ABC中，D是BC延长线上一点， ‎ ‎∠B = 40°，∠ACD = 120°，则∠A等于 A．60° B．70° ‎ C．80° D．90°‎ ‎（2010年安徽）14. 如图，AD是△ABC的边BC上的高，由下列条件中的某一个就能推出△ABC是等腰三角形的是__②____③___④________。（把所有正确答案的序号都填写在横线上）‎ ‎①∠BAD＝∠ACD ②∠BAD＝∠CAD，‎ ‎③AB+BD＝AC+CD ④AB-BD＝AC-CD ‎（第15题）‎ ‎（2010河南）15．如图，Rt△ABC中，∠C=90°，∠ABC=30°，AB=6．点D在AB边上，点E是BC边上一点（不与点 B、C重合），且DA=DE，则AD的取值范围是___________________．‎ ‎2≤AD＜3‎ ‎1、（2010山东烟台）如图，等腰△ ABC中，AB=AC，∠A=20°。线段AB的垂直平分线交AB于D，交AC于E，连接BE，则∠CBE等于 A、80° B、 70° C、60° D、50°‎ 答案：C ‎（2010·珠海）9.如图，P是菱形ABCD对角线BD上一点，PE⊥AB于点E，PE＝‎4cm，‎ 则点P到BC的距离是_____cm. 4‎ ‎（2010·珠海）12.如图，在梯形ABCD中，AB∥CD ‎（1）用尺规作图方法，作∠DAB的角平分线AF（只保留作图痕迹，不写作法和证明）‎ ‎（2）若AF交CD边于点E，判断△ADE的形状（只写结果）‎ 解：(1)所以射线AF即为所求 ‎(2)△ADE是等腰三角形.‎ ‎（益阳市2010年中考题8）．如图3，已知△ABC，求作一点P，使P到∠A的两边的距离相等，且PA＝PB．下列 确定P点的方法正确的是 Ａ．P为∠A、∠B两角平分线的交点　‎ Ｂ．P为∠A的角平分线与AB的垂直平分线的交点 Ｃ．P为AC、AB两边上的高的交点　　‎ Ｄ．P为AC、AB两边的垂直平分线的交点 答案：B ‎（益阳市2010年中考题11）．如图，在△ABC中，AB＝AC＝8，AD是底边上的高，E为AC中点，则DE＝　　　．‎ 答案：4‎ 益阳第11题图 ‎(苏州2010中考题7)．如图，在△ABC中，D、E两点分别在BC、AC边上．‎ ‎ 若BD=CD，∠B=∠CDE，DE=2，则AB的长度是 ‎ A．4 B．5‎ ‎ C．6 D．7‎ 答案：A ‎(苏州2010中考题10)．如图，已知A、B两点的坐标分别为(2，0)、(0，2)，⊙C的圆心坐标为(－1，0)，半径为1．若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值是 ‎ A．2 B．‎1 ‎‎ C． D．‎ 答案：C ‎(苏州2010中考题23)．(本题满分6分)如图，C是线段AB的中点，CD平分∠ACE，CE平分∠BCD，CD=CE．‎ ‎(1)求证：△ACD≌△BCE；‎ ‎(2)若∠D=50°，求∠B的度数．‎ ‎(苏州2010中考题25)．(本题满分8分)如图，在△ABC中，∠C=90°，AC=8，BC=6．P是AB边上的一个动点(异于A、B两点)，过点P分别作AC、BC边的垂线，垂足为M、N．设AP=x．‎ ‎ (1)在△ABC中，AB= ▲ ；‎ ‎ (2)当x= ▲ 时，矩形PMCN的周长是14；‎ ‎(3)是否存在x的值，使得△PAM的面积、△PBN的面积与矩形PMCN的面积同时相等?请说出你的判断，并加以说明．‎ ‎11. （莱芜）一个边长为2的正多边形的内角和是其外角和的2倍，则这个正多边形的半径是（ A ）‎ ‎ A．2 B． C．1 D． ‎1．（2010，安徽芜湖）下列命题是真命题的是（ ）‎ A．对角线互相垂直且相等的四边形是正方形 ‎ B．有两边和一角对应相等的两个三角形全等 ‎ C．两条对角线相等的平行四边形是矩形 ‎ D．两边相等的平行四边形是菱形 ‎【答案】C ‎2．（2010，浙江义乌）下列长度的三条线段能组成三角形的是 A．1、2、3.5 B．4、5、‎9 ‎ C．20、15、8 D．5、15、8‎ ‎【答案】C ‎3．（2010，浙江义乌）如图，直线CD是线段AB的垂直平分线，P为直线CD上的一点，已知线段PA＝5，则线段PB的长度为 A．6 B．‎5 ‎ C．4 D． 3‎ ‎【答案】B ‎4． （2010，浙江义乌）如图，将三角形纸片ABC沿DE折叠，使点A落在BC边上的点F处，且DE∥BC，下列结论中，一定正确的个数是 ‎①△BDF是等腰三角形 ②DE＝BC ‎③四边形ADFE是菱形 ④‎ A．1 B．‎2 ‎ C．3 D．4‎ ‎ A B C D E F ‎【答案】C ‎5．（2010，安徽芜湖）芜湖国际动漫节期间，小明进行了富有创意的形象设计。如图1，他在边长为1的正方形ABCD内作等边三角形BCE,并与正方形的对角线交于F、G点，制成如图2的图标。则图标中阴影图形AFEGD的面积=_____．‎ ‎【答案】-‎ ‎6．（2010，浙江义乌）如图1，已知∠ABC＝90°，△ABE是等边三角形，点P为射线BC上任意一点（点P与点B不重合），连结AP，将线段AP绕点A逆时针旋转60°得到线段AQ，连结QE并延长交射线BC于点F.‎ ‎（1）如图2，当BP＝BA时，∠EBF＝　▲　°，猜想∠QFC＝ ▲ °；‎ ‎（2）如图1，当点P为射线BC上任意一点时，猜想∠QFC的度数，并加以证明；‎ ‎（3）已知线段AB＝，设BP＝，点Q到射线BC的距离为y，求y关于的函数关系式．‎ 图1‎ A C B E Q F P 图2‎ A B E Q P F C ‎ 图3‎ ‎【答案】（1） 30°.＝ 60° 　　 ‎ ‎（2）＝60°‎ 不妨设BP＞, 如图1所示 ‎∵∠BAP＝∠BAE+∠EAP＝60°+∠EAP ‎ ‎∠EAQ＝∠QAP+∠EAP＝60°+∠EAP ‎∴∠BAP＝∠EAQ ‎ 在△ABP和△AEQ中 AB＝AE，∠BAP＝∠EAQ， AP＝AQ ‎∴△ABP≌△AEQ（SAS）‎ ‎∴∠AEQ＝∠ABP＝90°‎ ‎∴∠BEF ‎∴＝∠EBF +∠BEF ＝30°+30°＝60°‎ ‎ (事实上当BP≤时，如图2情形，不失一般性结论仍然成立，不分类讨论不扣分）(3) 在图1中，过点F作FG⊥BE于点G ‎∵△ABE是等边三角形 ‎∴BE＝AB＝，由（1）得30°‎ 在Rt△BGF中， ∴BF＝ ∴EF＝2‎ ‎∵△ABP≌△AEQ ∴QE＝BP＝ ∴QF＝QE＋EF 过点Q作QH⊥BC，垂足为H 在Rt△QHF中，（x＞0）‎ 即y关于x的函数关系式是：‎