20184泰安市中考数学样题一模答案 6页

‎2018年中考数学一模答案 一、选择题（本大题共12小题，在每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来，每小题选对得3分，错选、不选或选出的答案超过一个，均记零分）‎ ‎1-5 ACBBA 6-10 CADDD 11-12 BC ‎ 二、填空题（本大题共6小题，满分18分。只要求填写最后结果，每小题填对得3分）‎ ‎13. 14. 131° 15. 16.m≥2 17.50 18. 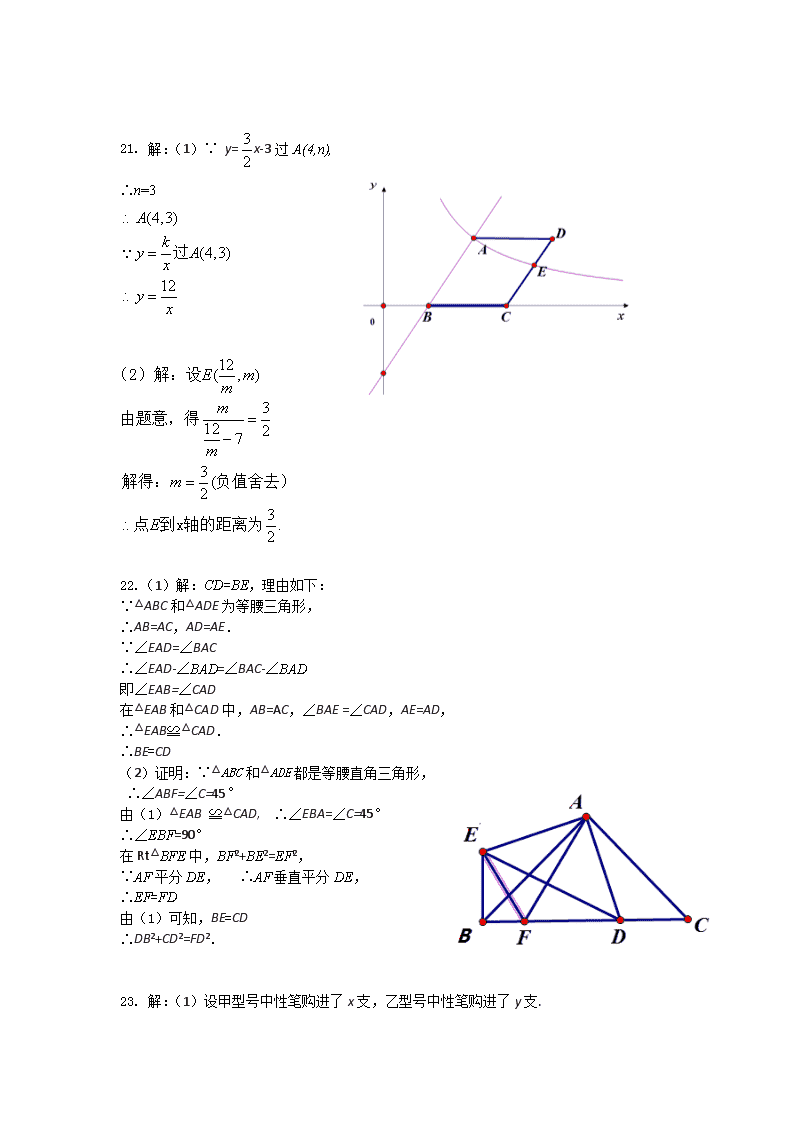‎ 三、解答题（共7小题，满分66分.解答应写出必要的文字说明、证明过程或推演步骤）‎ ‎19（本小题满分6分）‎ 解：先化简，再求值：，其中．‎ 当时，‎ 原式=‎ ‎20.（本小题满分8分 ‎ 解：（1）根据统计表与扇形统计图，可知D等级的有8人，占20%，‎ ‎∴参加比赛的共有8÷20%=40（人）．‎ ‎∴C等级为40-6-10-8=16（人）．‎ ‎∴A等级所占圆心角为．‎ 答：m=40，A等级所占圆心角为 ‎（2） ‎ ‎21. 解：（1）∵ y=x-3过A(4,n),‎ ‎∴n=3‎ ‎22.（1）解：CD=BE，理由如下：‎ ‎∵△ABC和△ADE为等腰三角形，‎ ‎∴AB=AC，AD=AE．‎ ‎∵∠EAD=∠BAC ‎∴∠EAD-∠BAD=∠BAC-∠BAD ‎ 即∠EAB=∠CAD 在△EAB和△CAD中，AB=AC，∠BAE =∠CAD，AE=AD，‎ ‎∴△EAB≌△CAD．‎ ‎∴BE=CD ‎（2）证明：∵△ABC和△ADE都是等腰直角三角形， ‎ ‎ ∴∠ABF=∠C=45° ‎ 由（1）△EAB ≌△CAD, ∴∠EBA=∠C=45° ‎ ‎∴∠EBF=90°‎ 在Rt△BFE中，BF2+BE2=EF2，‎ ‎∵AF平分DE， ∴AF垂直平分DE，‎ ‎∴EF=FD 由（1）可知，BE=CD ‎∴DB2+CD2=FD2．‎ ‎23. 解：（1）设甲型号中性笔购进了x支，乙型号中性笔购进了y支.‎ 由题意，得 解得 所以，甲型号中性笔购进了3000支，乙型号中性笔购进了1000支. ‎ ‎（2）设每支甲型号中性笔的利润为z元，则每支乙型号中性笔的利润为1.8z元.‎ 由题意，得，‎ 解得，又3+1.5=4.5.‎ 所以，每支甲型号中性笔的售价至少为4. 5元. ‎ ‎24.‎ ‎25.解：解：（1）将x=0代入抛物线的解析式得：y=2．‎ ‎∴C（0，2）．‎ ‎∵OBCD为矩形，‎ ‎∴OA=CD=1．‎ ‎∴A（－1，0）．‎ 又∵AB=4，‎ ‎∴B（3，0）．‎ 设抛物线的解析式为y=a（x－3）（x+1）．‎ 将点C的坐标代入得：－3a=2，解得：a=－，‎ ‎∴抛物线的解析式为y=－x2+x+2．‎ ‎（2）∵点E在CD上，‎ ‎∴yE=2．‎ 将y=2代入得：－x2+x+2=2，解得x=0或x=2．‎ ‎∴E（2，2）．‎ ‎∴EC=OC=2‎ ‎∴∠COE=45°．‎ ‎∵PG∥y轴，‎ ‎∴∠PGH=∠COE=45°．‎ 又∵PH⊥OE，‎ ‎∴PH=PG．‎ 设OE的解析式为y=kx，将点E的坐标代入得：2k=2，解得：k=1，‎ ‎∴直线OE的解析式为y=x．‎ ‎∴设点P的坐标为（m，－m2+m+2），则点G的坐标为（m，m）．‎ ‎∴PG=－m2+m+2－m=－m2+m+2．‎ ‎∴PH=×（－m2+m+2）=－m2+m+．‎ ‎=－(m－)2+．‎ ‎∴PH的最大值为．‎ ‎（3）抛物线的对称轴为x=－=1，设点N的坐标为（1，a），点M的坐标为（x，y）．‎ 过点M 作MQ⊥对称轴，垂足为Q，由AAS易证△MNO≌△ACO，‎ ‎∴QN=OC=2，MQ=AO=1，点M的横坐标为2，代入抛物线y=－x2+x+2．‎ 得y=－×4+×2+2=2 ∴点M的坐标为（2,2）‎ ‎∴N的横坐标为2－2=0．‎ ‎∴点N的坐标为（1,0）‎