中考最值问题大全2019 14页

中考最值问题解题策略 垂线段最短在最值问题中的应用 模型一 点到直线的所有线段中，垂线段最短 A B O M 点P在直线l外，过点P作l的垂线PH，垂足为H，则点P到直线l的最短距离为线段PH的长，即“垂线段最短”．‎ ‎1、如图，⊙O的半径为5，弦AB＝6，M是AB上任意一点，则线段 OM的取值范围是_______________。‎ ‎2、如图，在锐角△ABC中，BC＝4，∠ABC＝45°，BD平分∠ABC，‎ M、N分别是BD、BC上的动点，则CM＋MN的最小值是________．‎ ‎3. 如图，在Rt△AOB中，OA＝OB＝3，⊙O的半径为1，点P 是AB边上的动点，过点P作⊙O的一条切线PQ(点Q为切点)，‎ 则线段PQ的最小值为________．‎ 模型二 “胡不归”问题 基本模型：两定一动，动点在定直线上 问题：点A为直线l上一定点，点B为直线外一定点，P为直线l上一动点，要使AP＋BP最小．‎ 解决：过点A作∠NAP＝45°，过点P作PE⊥AN，在直角三角形中将AP转化为PE，使得AP＋BP＝PE＋BP，然后利用“两点之间线段最短”将“折”变“直”，再利用“垂线段最短”转化为求BF的长度．‎ 此类题的解题步骤：第一步：以系数不为1的线段的定端点为顶点作一个角，使其正弦值等于此线段的系数(注意题目中有无特殊角)；‎ 第二步：过动点作第一步中角的边的垂线，构造直角三角形；‎ 第三步：根据两点之间线段最短，将“折”变“直”，再利用 ‎“垂线段最短”找到最小值的位置．‎ ‎4. 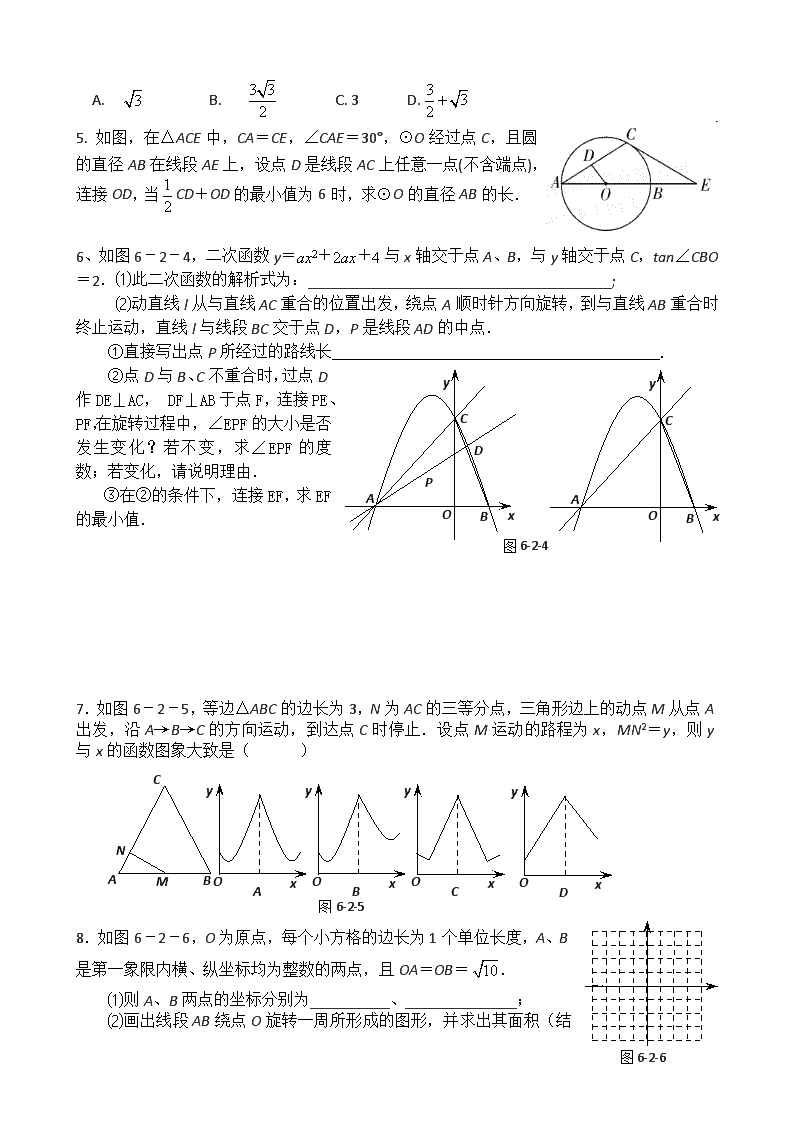如图，菱形ABCD中，∠ABC＝60°，边长为3，P是对角线 BD上的一个动点，则BP＋PC的最小值是( )‎ ‎ A. B. C. 3 D.‎ ‎5. 如图，在△ACE中，CA＝CE，∠CAE＝30°，⊙O经过点C，且圆的直径AB在线段AE上，设点D是线段AC上任意一点(不含端点)，连接OD，当CD＋OD的最小值为6时，求⊙O的直径AB的长．‎ ‎6、如图6－2－4，二次函数y＝ax2＋2ax＋4与x轴交于点A、B，与y轴交于点C，tan∠CBO＝2．⑴此二次函数的解析式为：______________________________________;‎ ‎⑵动直线l从与直线AC重合的位置出发，绕点A顺时针方向旋转，到与直线AB重合时终止运动，直线l与线段BC交于点D，P是线段AD的中点．‎ ‎ ①直接写出点P所经过的路线长_________________________________________.‎ A B O P x y C D A B O x y C 图‎6-2-4‎ ‎②点D与B、C不重合时，过点D作DE⊥AC， DF⊥AB于点F，连接PE、PF，在旋转过程中，∠EPF的大小是否发生变化？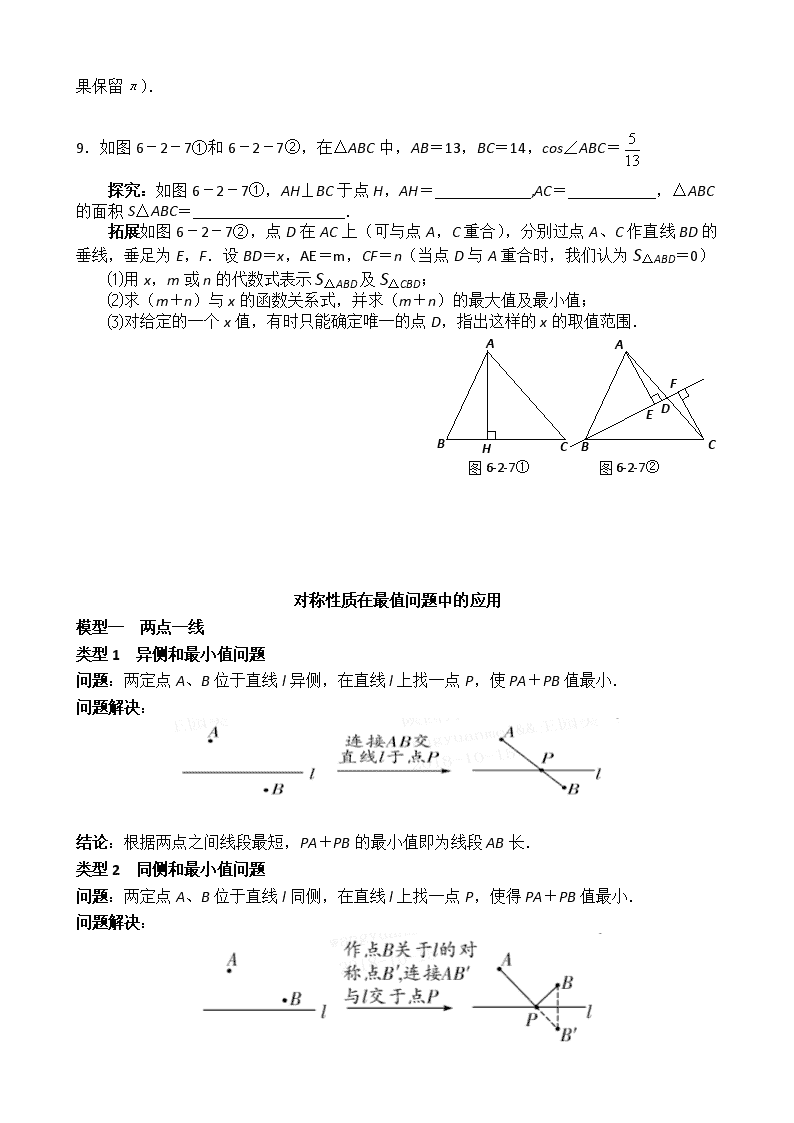若不变，求∠EPF的度数；若变化，请说明理由．‎ ‎③在②的条件下，连接EF，求EF的最小值．‎ ‎7．如图6－2－5，等边△ABC的边长为3，N为AC的三等分点，三角形边上的动点M从点A出发，沿A→B→C的方向运动，到达点C时停止．设点M运动的路程为x，MN2＝y，则y与x的函数图象大致是（ ）‎ 图‎6-2-6‎ A B C M N O A x y O B x y O C x y O D x y 图‎6-2-5‎ ‎8．如图6－2－6，O为原点，每个小方格的边长为1个单位长度，A、B是第一象限内横、纵坐标均为整数的两点，且OA＝OB＝．‎ ‎⑴则A、B两点的坐标分别为__________、______________；‎ ‎⑵画出线段AB绕点O 旋转一周所形成的图形，并求出其面积（结果保留π）．‎ ‎9．如图6－2－7①和6－2－7②，在△ABC中，AB＝13，BC＝14，cos∠ABC＝‎ 探究：如图6－2－7①，AH⊥BC于点H，AH＝____________,AC＝___________，△ABC的面积S△ABC＝___________________．‎ 拓展如图6－2－7②，点D在AC上（可与点A，C重合），分别过点A、C作直线BD的垂线，垂足为E，F．设BD＝x，AE＝m，CF＝n（当点D与A重合时，我们认为S△ABD＝0）‎ ‎⑴用x，m或n的代数式表示S△ABD及S△CBD；‎ ‎⑵求（m＋n）与x的函数关系式，并求（m＋n）的最大值及最小值；‎ ‎⑶对给定的一个x值，有时只能确定唯一的点D，指出这样的x的取值范围．‎ A B C H A B C D F E 图‎6-2-7‎①‎ 图‎6-2-7‎②‎ 对称性质在最值问题中的应用 模型一 两点一线 类型1 异侧和最小值问题 问题：两定点A、B位于直线l异侧，在直线l上找一点P，使PA＋PB值最小．‎ 问题解决：‎ 结论：根据两点之间线段最短，PA＋PB的最小值即为线段AB长．‎ 类型2 同侧和最小值问题 问题：两定点A、B位于直线l同侧，在直线l上找一点P，使得PA＋PB值最小．‎ 问题解决：‎ 结论：将两定点同侧转化为异侧问题，PA＋PB最小值为AB′．‎ 类型3 同侧差最小值问题 问题：两定点A、B位于直线l同侧，在直线l上找一点P，使得|PA－PB|的值最小．‎ 问题解决：‎ 结论：根据垂直平分线上的点到线段两端点的距离相等，当PA＝PB时，|PA－PB|＝0. ‎ 类型4 同侧差最大值问题 问题：两定点A、B位于直线l同侧，在直线l上找一点P，使得|PA－PB|的值最大．‎ 问题解决：‎ 结论：根据三角形任意两边之差小于第三边，|PA－PB|≤AB，则|PA－PB|的最大值为线段AB的长．‎ 类型5 异侧差最大值问题 问题：两定点A、B位于直线l异侧，在直线l上找一点P，使得|PA－PB|的值最大．‎ 问题解决：‎ 结论：将异侧点转化为同侧，同类型4，|PA－PB|的最大值为AB′. ‎ ‎1.如图，正方形ABCD的边长为8，点M在边DC上，且DM＝2，点N是对角线AC上一动点，则线段DN＋MN的最小值为________．‎ ‎2.如图，点C的坐标为(3，y)，当△ABC的周长最小时，‎ 则y的值为________．‎ ‎3.如图，已知△ABC为等腰直角三角形，AC＝BC＝4，∠BCD＝15°，‎ P为射线CD上的动点，则|PA－PB|的最大值为________．‎ A B C D P E A B C D P M N A C B D E P 图‎6-1-1‎③ ‎ 图‎6-1-1‎④ ‎ 图‎6-1-1‎⑤ ‎ ‎4、如图6－1－1④，已知菱形ABCD的两条对角线分别为6和8，M、N分别是BC、CD的中点，P是对角线BD上一点，则PM＋PN的最小值＝ .‎ ‎5、如图6－1－1⑤，在Rt△ABC中，∠C＝90°，∠B＝60°，点D是BC边上的点，CD＝，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则△PEB的周长的最小值是 .‎ ‎6.（1）如图6－1－2①，在等边△ABC中，AB＝6，点E是AB的中点，AD是高，在AD上找一点P，使PB＋PE的值最小，最小值为 .‎ ‎（2）如图6－1－2②，⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC＝60°，P是OB上一动点，则PA＋PC的最小值是 ；‎ B C A D E P D A B C E A O B C P 图‎6-1-2‎③ ‎ 图‎6-1-2‎② ‎ 图‎6-1-2‎① ‎ ‎ （3）如图6－1－2③，点D、E分别是△ABC的AC、AB边的中点，BC＝6，BC边上的高为4，P在BC边上，则△PDE周长的最小值为 .‎ ‎7.（1）如图6－1－3①，Rt△OAB的顶点A在x轴的正半轴上，顶点B的坐标为（3，），点C的坐标为（1，0），点P 为斜边OB上的一动点，则PA＋PC的最小值为 .‎ ‎（2）如图6－1－3② ，菱形ABCD中AB＝2，∠A＝120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK＋QK的最小值为 .‎ A C D B M N 图‎6-1-3‎③ ‎ x P B C A O y 图‎6-1-3‎① ‎ A D C B K P Q 图‎6-1-3‎② ‎ ‎（3）如图6－1－3③，锐角△ABC中，AB＝4，∠BAC＝45°，AD平分∠BAC，‎ M、N分别是AD和AB上的动点，则BM＋MN的最小值是 .‎ ‎8.（1）如图6－1－4①，∠AOB＝45°，P是∠AOB内一点，PO＝10，Q、R分别是OA、OB上的动点，则△PQR周长的最小值是 .‎ ‎（2）如图6－1－4②，点A（a，1）、B（－1，b）都在双曲线y＝(x<0)上，点P、Q分别是x轴、y轴上的动点，当四边形PABQ的周长取最小值时，PQ在直线的解析式是（ ）.‎ A.y＝x B.y＝x＋‎1 C.y＝x＋2 D.y＝x＋3‎ A B O P R Q A P Q O ‎ B y x B A a b 图‎6-1-4‎① ‎ 图‎6-1-4‎② ‎ 图‎6-1-5‎ ‎ A A C D O P x y 图‎6-1-13‎③ ‎ ‎9. 如图6－1－5已知，直线a∥b，且a与b之间的距离为4，点A到直线a的距离为2，点B到直线b的距离为3，AB＝2，试在直线a上找一点M，在直线b上找一点N，满足MN⊥a且AM＋MN＋NB的长度和最短，则此时AM＋NB＝（ ）‎ A.6 B‎.8 C.10 D.12‎ ‎10、如图6－1－13③，一次函数y＝－2x＋4的图象与x、y轴分 别交于点A，B，D 为AB的中点，C、A关于原点对称．P为OB 上一动点，请直接写出︱PC－PD︱的范围：__________________．‎ ‎11．如图6－1－14，在平面直角坐标系xOy中，已知点A（0，1），B（1，2），点P在x轴上运动，当点P到A、B两点距离之差的绝对值最大时，点P的坐标是____________________．‎ ‎12．在⊙O所在的平面上有一点A，它到⊙O的最近距离是3，最远距离是7，则⊙O的半径为________________．‎ ‎13．在A、B均在面积为1的小正方形组成的网格的格点上，建立平面直角坐标坐标系如图6－1－15，若P是x轴上使得︱PA－PB︱的值最大的点，OP＝__________________.‎ O x y A B B A O y x x y A B C O 图‎6-1-14‎ 图‎6-1-15‎ 图‎6-1-16‎ ‎14．如图6－1－16，抛物线y＝ax2＋bx－‎4a经过A(－1,0)、C(0,4)两点，与x轴交于另一 点B．⑴抛物线及对称轴分别为________________________________;‎ ‎⑵点D所在抛物线的对称轴上，求︱DB－DC︱的最大值．‎ 模型二 一点两线 类型1 一定点与两条直线上两动点问题 问题：点P在∠AOB的内部，在OB上找一点D，在OA上找一点C，使得△PCD周长最小．‎ 问题解决：‎ 结论：要使△PCD周长最小，即PC＋PD＋CD值最小，根据两点之间线段最短，将三条线段转化到同一直线上即可，则△PCD周长最小为线段的长．‎ 类型2 两定点与两条直线上两动点问题 问题：点P、Q在∠AOB的内部，在OB上找点D，在OA上找点C，使得四边形PQDC周长最小．‎ 问题解决：‎ 结论：将问题转化为类型1即可，PC＋CD＋DQ的最小值为线段P’Q’长，则四边形PQDC的周长的最小值为P’Q’＋PQ的值．‎ ‎1.如图，四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC，CD上分别找一点M，N使△AMN的周长最小，则∠AMN＋∠ANM的度数为________．‎ ‎2.如图，在直角坐标系中，已知A(－3，－1)，B(－1，－3)，若D是x轴上一动点，C是y轴上的一个动点，则四边形ABCD的周长的最小值是________．‎ A B C D A′‎ B′‎ C′‎ D′‎ 图6－1－6① ‎ 模块四 “小虫爬行问题”‎ 例6－1－2（1）如图6－1－6①，已知长方体的长为AC＝‎2cm，宽BC＝‎1cm，高AA′＝‎4cm，一只蚂蚁沿长方体的表面从A点爬到B′点的最短路径是多少？‎ ‎【规律】“小小相加凑一边时路径最短.” ‎ A′‎ C′‎ 蚂蚁 ‎ 蜜蜂 ‎ ‎（2）如图6－1－6②，圆柱形杯高为‎12cm、底面 周长为18cm，在杯内离杯底4cm的点C处有一滴 蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm 与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离 为多少cm?‎ ‎【规律】“一点内一点外要用轴对称.”‎ 练习：‎ ‎1.（1）如图6－1－7①，长方体的长宽高分别为15、10、20，点B离点C的距离为5，一只蚂蚁沿着长方体的表面从点A爬到点B，最短距离是（ ）‎ A C B E′‎ G′‎ H′‎ A′‎ B′‎ B′‎ A′‎ C′‎ O′‎ A′‎ C′‎ ‎15‎ ‎5‎ F′‎ ‎20‎ B′‎ 图‎6-1-7‎① ‎ A.5 B‎.25 C.10＋5 D.35‎ 图‎6-1-7‎②‎ 图‎6-1-7‎ ③ ‎ 图‎6-1-7‎④ ‎ ‎（2）6－1－7②，底面半径为3cm的圆锥的主视图是个正三角形，C是母线OB的中点，则从圆锥表面从A到C的最短距离等于 cm.‎ ‎（3）6－1－7③,圆柱高‎8cm，底面半径‎2cm，一只蚂蚁从点A爬到点B处吃食，爬行的最短路程（π取3）是（ ）cm.‎ A.20 B‎.10 C.14 D.无法确定 ‎（4）如图6－1－7④，ABCDEFGH是个无上底长方体容器，M在容器内侧，位于侧棱BF上，已知AB＝5，BF＝9，FM＝3，则从外部的点A到内部的点M的最短距离等于 .‎ A′‎ B′‎ ‎20‎ ‎3‎ ‎2‎ ‎2.如图6－1－8，是一个三级台阶，它的每一级的长、宽、高分别为20dm，3dm，2dm，A和B是这个台阶两相对的端点，A点有一只昆虫想到B点去吃可口的食物，则昆虫沿着台阶爬到B点的最短路程是多少dm？ ‎ 图6－1－8 ‎ 模块五 折叠最值 A′‎ B′‎ C′‎ D′‎ ‎【规律】折叠背景下的最值问题，考查的是动手操作能力、合情推理能力.方法是：‎ ‎（1）在折叠中感受大小变化规律，（2）通过特殊位置求最值.‎ ‎1、如图6－1－9，折叠矩形纸片ABCD，使B点落在AD上一点E处，折痕的两端点M、N分别在AB、BC上（含端点），且AB＝6，BC＝10，设AE＝x，则x的取值范围是 .‎ B′‎ A′‎ D′‎ C′‎ P′‎ Q′‎ A′‎ 图6－1－9‎ ‎【规律】A、E重合时x最小为0，折痕的两端点在AB、CD上，不合题意，向下移动N到C时，得x的最小值，继续沿BC向B移动N，使M上移至A时，得到满足条件的x最大值；‎ A B C F E D 图‎6-3-1‎ 图6－1－11‎ ‎2.动手操作：在矩形纸片ABCD中，AB＝3，AD＝5，如图6－1－11，折叠纸片，使点A落在BC边上的A′处，折痕为PQ，当点A′在BC边上移动时，折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动，则点A′在BC边上可移动的最大距离为 .‎ 模块六 圆中最长弦是直径 解法归一：求对角是直角的双直角四边形中对角线的最小值、或圆中线段最小值时常用它．‎ 图‎6-3-2‎ A B C G H E F O ‎1、如图6－3－1，等腰直角△ABC斜边长为4，D为是斜边AB的中点，直角∠FDE分别交AC、BC于F、E，则线段EF的最小值是_________________．‎ ‎2．如图6－3－2，AB是⊙O的一条弦，点C是⊙O上一动点，且 ‎∠ACB＝30°，点E、F分别是AC、BC的中点，直线EF与⊙O交点 G、H两点，若⊙O的半径为6，则GE＋FH的最大值为____________．‎ 模块七、求两正数和的最小值[9]‎ 解法：①由（a－b）2≥0得a2＋b2≥2ab，当且仅当a＝b时成立；‎ ‎②对任意正数m,n可设m＝a2、n＝b2(a、b为正数)，则有m＋n＝a2＋b2≥2ab＝2，‎ 即m＋n≥2，当且仅当m＝n时等号成立．‎ 这是高中两个最重要的不等式．求两个正数和的最小值时就用它，并且只有这两个正数相等时和才取最小值．‎ ‎1、阅读理解：对任意实数a，b，‎ ‎∵（－）2≥0，∴a－2＋b≥0，∴a＋b≥2，只有当a＝b时，等号成立．‎ 根据上述内容，回答下列问题：‎ ‎⑴若m＞0，只有m＝____时m＋有最小值______________；‎ ‎⑵若n＞0，只有n＝_____时n＋有最小值_____________；‎ ‎⑶若x＞0，只有x＝______时，8x2＋有最小值___________________;‎ B A C D O 图‎6-4-1‎ ‎2、如图6－4－1，AB为半圆O的直径，C为半圆上与点A、B不重合的任意一点，过点C作CD⊥AB，垂足为D，AD＝a，DB＝b．请用本题图验证a＋b≥2,并指出等号成立时的条件．‎ A B C D P x y O 图‎6-4-2‎ ‎3、如图6－4－2，已知A（－3，0），B（0，－4），P为双曲线y＝(x＞0)上任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D，求四边形ABCD的面积的最小值，并说明此时四边形ABCD的形状．‎ ‎4、公式：对于任意正数a、b，总有a＋b≥2，并且只有当a＝b时，等号成立．‎ 直接应用或变形应用 ‎⑴已经y1＝x（x＞0），y2＝（x＞0），则当x＝____________时，y1 ＋y2取得最小值___________.‎ ‎⑵已知函数y＝x＋(a＞0，x＞0)，当x＝______________时，该函数有最小值_____________．‎ ‎⑶已知函数y1＝x＋1与函数y2＝(x＋1)2＋4，当x＞－1时，求的最小值，并指出相应的x的值．‎ 实际应用 已知某汽车的一次运输成本包含以下三个部分：一是固定费用，共360元；二是燃油费费，每千米为1.6元；三是折旧费，它与路程的平方成正比，比例系数为0.001．设汽车一次运输的路程为x千米，求当x为多少时，该汽车平均每千米的运输成本最低？最低是多少元？‎ 模块八 二次函数最值 解法归一：“二次整数ax2＋bx＋c最值”完全可以借助二次函数y＝ax2＋bx＋c最值解决，解决方案有三：一用配方法，二用顶点公式，三图象法．（注：a,b,c为常数，且a≠0）‎ ‎1、 ⑴x2－2x＋6的最小值是_______________________;‎ ‎⑵二次函数y＝－x2＋6x的最大值是______________________．‎ A B C D E P 图‎6-6-1‎ ‎2、如图6－6－1，在矩形ABCD中，AB＝2，AD＝3，P是BC上任意一点（P不与B、C重合），过点P作AP⊥PE交CD于点Ｅ．设BP为x，CE为y，当x取何值时，y的值最大？最大值是多少？‎ A B C ‎4‎ ‎1‎ ‎5‎ O l y x M 图‎6-6-2‎ ‎3、如图6－6－2，已知抛物线y＝ax2＋bx＋4经过点B（1，0），C（5，0），交纵轴于点A，对称轴l与x轴相交于点M．‎ ‎⑴请直接写出抛物线的解析式，对称轴及点A的坐标;‎ ‎⑵在此抛物线的对称轴上是否存在一点P，使△PAB的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由；‎ ‎（3）连接AC，在直线AC的下方的抛物线上，是否存在一点N，使△NAC的面积最大？若存在，请求出点N的坐标；若不存在，请说明理由.‎ A B C D M N F E 图‎6-6-3‎ ‎4、如图6－6－3，把一张边长为4的正方形ABCD折叠，使B点落在AD上的E处，折痕为MN，设AE＝x，问x为何值时，折起的四边形MNFE面积最小，并求出这个最小面积的值．‎ 模块九 几何探究最值类[8]‎ ‎1、请阅读下列材料：问题：如图6－7－1①，圆柱的高AB和它的底面半径均为5dm，BC是底面直径，求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线．‎ 小明设计了两条路线：‎ 路线1：走圆柱表面最短路线（即图6－7－1②侧面展开图中的线段AC）．‎ 路线2：走圆柱高线与度面直径（即图6－7－1①中的AB＋BC的长）‎ A B C D A B C D 图‎6-7-1‎①‎ 图‎6-7-1‎②‎ 沿AB剪开 摊平 此长方形的长等于底面周长 设路线1的长度为l1，设路线2的长度为l2，则l12＝AC2＝AB2＋ l22＝(AB＋BC)2，将AB＝5，BC＝10，半圆弧长5π代入上面的式子得（请你帮小明完成下面的计算）：‎ l12＝AC2＝ ；‎ l22＝(AB＋BC)2＝ ；‎ l12－l22＝ .‎ ‎∴l12>l22 ∴l1>l2 ∴选择路线2较短.‎ ‎ （1）小明对上述问题结论有些疑惑，于是他把条件改成：“圆柱的底面半径为1dm,高AB为5dm”继续按前面的路线进行计算（请你帮小明完成下面的计算）：‎ ‎ 路线1：l12＝AC2＝ ；‎ 路线2：l22＝(AB＋BC)2＝ ；‎ ‎∵l‎12 l22，∴l‎1 l2（填>或<），所以选择路线 （填1或2）较短.‎ ‎（2）请你帮小明继续研究：在一般情况下，当圆柱的底面半径为r，高为h时，应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短.‎ ‎2、在河岸l同侧有A、B两个村庄，A、B到l的距离分别是‎3km和‎2km，AB＝akm(a>1)现计划在河岸上建一抽水站P向两个村庄供水.‎ 方案设计：某班数学兴趣小组设计了两种管道铺设方案：‎ 图6－7－2①是方案一的示意图，设该方案中管道长度为d，且d1＝PB＋BA(km)(其中PB⊥l于P点)；‎ 图6－7－2②是方案二的示意图，设该方案中管道长度为d2,且d2＝PA＋PB(km)(其中点A′与点A关于l对称，A′B与l交于点P).‎ A B l 图‎6-7-2‎① ‎ A B l 图‎6-7-2‎② ‎ A B l 图‎6-7-2‎③ ‎ P C C K P A′‎ A′‎ P 观察与计算（1）在方案一中，‎ d1＝ km(用含a的式子表示)；‎ ‎（2）在方案二中，组长小宇为了计算d2的长，作了如图6－7－2③的辅助线，请你按小宇同学的思路计算，d2＝ km(用含a的式子表示).‎ 探索归纳：（1）①当a＝4时，比较大小：d1 d2（填“>”或“＝”或“<”）；‎ ‎②当a＝6时比较大小：d1 d2（填“>”或“＝”或“<”）；‎ ‎（2）请你就a（当a>1时）的所有取值情况进行分析，要使铺设的管道长度较短，应选择方案一还是方案二？‎ A′‎ B′‎ A′‎ B′‎ A′‎ B′‎ A’′‎ B’′‎ 图‎6-7-3‎① ‎ 图‎6-7-3‎② ‎ 图‎6-7-3‎③ ‎ ‎3、（1）如图6－7－3①，把矩形AA′ B′ B卷成以AB为高的圆柱形，则点A与 重合，点B与 重合.‎ 探究与发现 ‎ （2）如图6－7－3②所示，若圆柱的底面周长是‎30cm，高是‎40cm，从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处作装饰，则这条丝线的最小长度是 cm；（丝线的粗细忽略不计）‎ A′‎ B′‎ 图‎6-7-3‎④ ‎ ‎（3）若用丝线从图6－7－3②圆柱底部A处沿侧面缠绕4圈直到顶部B处（如图6－7－3③所示），则至少需要多长丝线？‎ ‎ 创新与应用：（4）如图6－7－3④，现有一圆柱形的玻璃杯，准备在杯子的外侧缠绕一层装饰带，为使带子的两端沿AE、CF方向进行裁剪，如图6－7－3⑤，若带子宽度为1.5厘米，杯子的半径为6厘米，裁剪角为α，则sinα＝ .‎ α′‎ α′‎ A′‎ B′‎ C′‎ D′‎ F′‎ E′‎ 图‎6-7-3‎⑤ ‎ ‎ 4、如图6－7－4①是一个三棱柱包装盒，它的底面是边长为‎10cm的正三角形，三个侧面都是矩形.现将宽为‎15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD（如图6－7－4②），然后用这条平行四边形纸带按如图6－7－4③的方式把这个三棱柱包装盒的侧面进行包贴（要求包贴时没有重合部分），纸带在侧面缠绕三圈，正好将这个三棱柱包装盒的侧面全部包贴满.‎ 图‎6-7-4‎③ ‎ A′‎ 图‎6-7-4‎① ‎ ‎ ‎A′‎ M′‎ B′‎ C′‎ N′‎ D′‎ 图‎6-7-4‎② ‎ ‎（1）请计算图6－7－4②中裁剪的角度∠BAD；‎ ‎（2）计算按图6－7－4③方式包贴这个三棱柱包装盒所需的矩形纸带的长度.‎