2007年中考数学丽水市试卷 12页

浙江省丽水市2007年初中毕业生学业考试 数　　学 考生须知：‎ ‎1、全卷满分为150分，考试时间为120分钟．‎ ‎2、全卷分“卷Ⅰ”和“卷Ⅱ”两部分，其中“卷Ⅰ”为选择题卷；“卷Ⅱ”为非选择题卷．‎ ‎3、答题前，请在答题卡上先填写姓名和准考证号，再用铅笔将准考证号和科目对应的括号或方框涂黑．‎ ‎4、请在“卷二”上填写座位号并在密封线内填写县（市、区）学校、姓名和准考证号．‎ ‎5、答题时，允许使用计算器．‎ 温馨提示：带着愉悦的心情，载着自信与细心，凭着沉着与冷静，迈向理想的彼岸！ ‎ 试 卷 Ⅰ 请用铅笔将答卷Ⅰ上的准考证号和学科名称所对应的括号或方框内涂黑，然后开始答题．‎ 一、选择题（本题有10小题，每小题4分，共40分．请选出各题中一个符合题意的正确选项，不选、多选、错选，均不给分）‎ ‎1. 2的相反数是 A.　2 B.　－‎2 C.　 D.　－‎ ‎（第2题）‎ A B C D ‎1‎ ‎2‎ ‎2．如图，∥，若∠1=45°，则∠2的度数是 ‎ A．45° B．90° ‎ ‎ C．30° D．135° ‎ ‎3．下列图形中，不是轴对称图形的是 ‎ ‎ ‎ ‎ ‎ ‎ A.　 B.　 C.　 D.　‎ ‎4．已知反比例函数，则这个函数的图象一定经过 A. (2，1) B. (2，-1) C. (2，4) D. 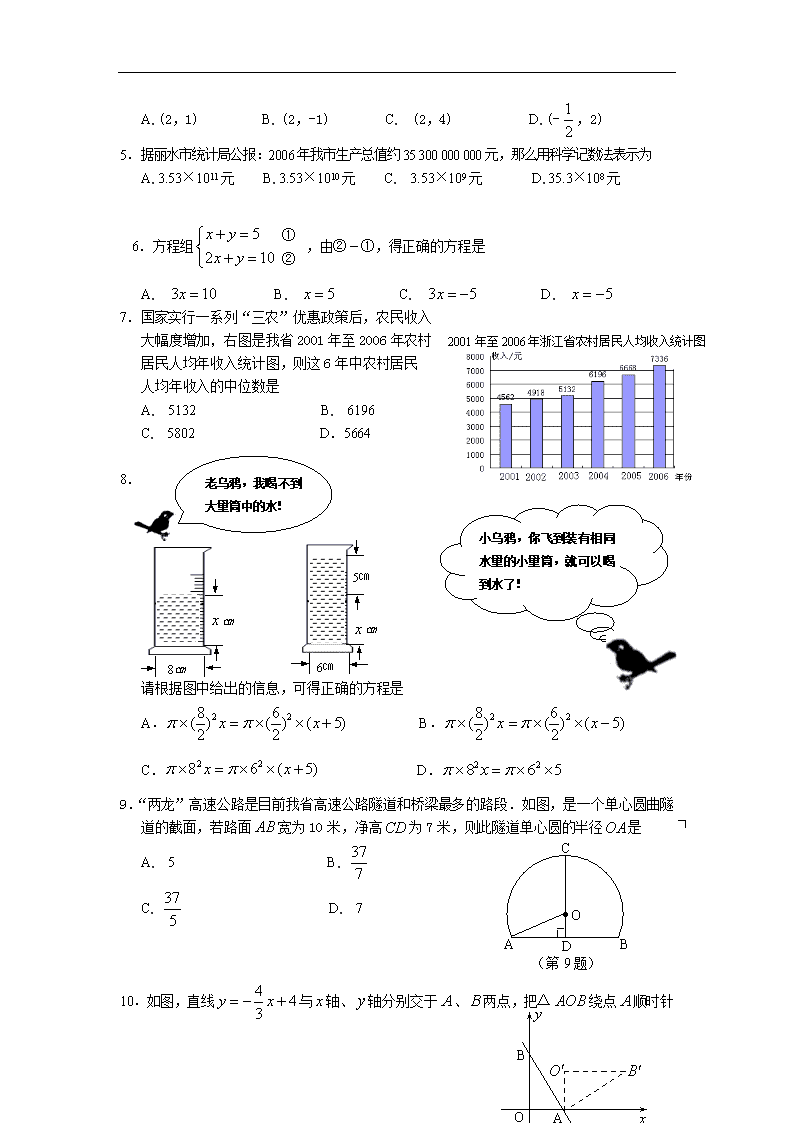(-，2)‎ ‎5．据丽水市统计局公报：2006年我市生产总值约35 300 000 000元，那么用科学记数法表示为 A. 3.53‎‎×1011元 B. 3.53×1010元 C. 3.53×109元 D. 35.3×108元 ‎②‎ ‎①‎ ‎6．方程组 ，由②①，得正确的方程是 A.　 B.　 C.　 D.　‎ ‎2001年至2006年浙江省农村居民人均收入统计图 ‎7．国家实行一系列“三农”优惠政策后，农民收入 大幅度增加，右图是我省2001年至2006年农村 居民人均年收入统计图，则这6年中农村居民 人均年收入的中位数是 A. 5132　 B. 6196　 ‎ ‎ C. 5802　 D．5664‎ ㎝ ‎5㎝ ‎6㎝ ‎8㎝ 老乌鸦，我喝不到大量筒中的水！‎ ㎝ ‎8．‎ 小乌鸦，你飞到装有相同水量的小量筒，就可以喝到水了！‎ 请根据图中给出的信息，可得正确的方程是 ‎ A． B．‎ C． D．‎ O D A B C ‎（第9题）‎ ‎9．“两龙”高速公路是目前我省高速公路隧道和桥梁最多的路段．如图，是一个单心圆曲隧道的截面，若路面宽为‎10米，净高为‎7米，则此隧道单心圆的半径是 A. 5 B. ‎ C. D.　7‎ A B O ‎（第10题）‎ ‎10．如图，直线与轴、轴分别交于、两点，把△绕点顺时针旋转90°后得到△，则点的坐标是 A. （3，4） B. （4，5）　 ‎ C. （7，4） D. （7，3）‎ 浙江省2007年初中毕业生学业考试（丽水市卷）‎ 数　　学 试卷Ⅱ 大题号 二 三 卷Ⅱ总分 小题号 ‎11～16‎ ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ ‎23‎ ‎24‎ 得 分 说明：本卷有二大题，14小题，共110分，请用蓝黑墨水的钢笔或圆珠笔直接在试卷上答题．‎ 得分 评卷人 二、填空题（本题有6小题，每小题5分，共30分）‎ ‎11．因式分解： ．‎ ‎（第14题）‎ A B C ‎12．当= 时，分式无意义．‎ ‎13．等腰三角形的一个底角为，则顶角的度数是 度．‎ ‎14．如图，一架梯子斜靠在墙上，若梯子到墙的距离=‎3米，‎ ‎，则梯子的长度为 米． ‎ ‎15． 如果一个立体图形的主视图为矩形，则这个立体图形可能是 （只需填上一个立体图形）．‎ O ‎16．廊桥是我国古老的文化遗产．如图，是某座抛物线型的廊桥示意图，已知抛物线的函数表达式为，为保护廊桥的安全，在该抛物线上距水面高为‎8米的点、处要安装两盏警示灯，则这两盏灯的水平距离是 米（精确到‎1米）．‎ 得分 评卷人 三、解答题（本题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）‎ ‎17．（本题8分）‎ ‎（1）计算：． （2）解不等式：＜．‎ ‎ ‎ 得分 评卷人 ‎18．（本题8分）‎ ‎ ‎ A ‎ ‎ B ‎ ‎ C ‎ ‎ D ‎ ‎ E ‎ ‎ F ‎ ‎ O ‎ ‎ 如图，矩形中，与交于点，⊥， ⊥，垂足分别为，．‎ 求证：．‎ 得分 评卷人 ‎19．（本题8分）‎ 如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是60°），菱形的边长为2，是的中点，按将菱形剪成①、②两部分，用这两部分可以分别拼成直角三角形、等腰梯形、矩形，要求所拼成图形的顶点均落在格点上．‎ ‎（1）在下面的菱形斜网格中画出示意图；‎ ‎（直角三角形）‎ ‎（等腰梯形）‎ ‎（矩形）‎ ‎（2）判断所拼成的三种图形的面积（）、周长（）的大小关系（用“=”、“＞”或“＜”连接）：‎ ‎ 面积关系是 ；‎ 周长关系是 ．‎ 得分 评卷人 ‎20．（本题8分）‎ 小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法，请你按有关内容补充完整：‎ 复习日记卡片 内容：一元二次方程解法归纳 时间：2007年6月×日 举例：求一元二次方程的两个解 方法一：选择合适的一种方法（公式法、配方法、分解因式法）求解 ‎ 解方程：．‎ ‎ 解：‎ 方法二：利用二次函数图象与坐标轴的交点求解 如图所示，把方程的解看成是二次 函数 的图象与轴交点的 横坐标，即就是方程的解.‎ 方法三：利用两个函数图象的交点求解 ‎ （1）把方程的解看成是一个二次函数 的图象与一个一次函数 图象交点的横坐标；‎ ‎1‎ ‎2‎ ‎4‎ ‎-2‎ ‎-3‎ ‎ （2）画出这两个函数的图象，用在轴上标出方程的解.‎ ‎3‎ ‎2‎ ‎1‎ ‎3‎ ‎-1‎ ‎-2‎ ‎-1‎ 得分 评卷人 ‎21．（本题10分）‎ ‎ 在课外活动时间，小王、小丽、小华做“互相踢踺子”游戏，踺子从一人传到另一人就记为踢一次．‎ ‎（1）若从小丽开始，经过两次踢踺后，踺子踢到小华处的概率是多少？（用树状图或列表法说明）‎ ‎（2）若经过三次踢踺后，踺子踢到小王处的可能性最小，应确定从谁开始踢，并说明理由．‎ 得分 评卷人 锻炼 ‎22．（本题12分）‎ 不喜欢 没时间 其它 原因 锻炼未超过1小时人数频数分布直方图 人数 ‎ 为了开展阳光体育运动，坚持让中小学生“每天锻炼一小时”，某县教研室体育组搞了一个随机调查，调查内容是：“每天锻炼是否超过1小时及锻炼未超过1小时的原因”，他们随机调查了720名学生，所得的数据制成了如下的扇形统计图和频数分布直方图．‎ 根据图示，请你回答以下问题：‎ ‎（1）“没时间”的人数是 ，并补全频数分布直方图；‎ ‎（2）2006年丽水市中小学生约32万人，按此调查，可以估计2006年全市中小学生每天锻炼未超过1小时约有 万人；‎ ‎（3）如果计划2008年丽水市中小学生每天锻炼未超过1小时的人数降到3.84 万人，求2006年至2008年锻炼未超过1小时人数的年平均降低的百分率是多少？‎ 得分 评卷人 ‎23．（本题12分）‎ 如图，⊙O的直径=‎6cm，是延长线上的一点，过点作⊙O的切线，切点为，连接．‎ ‎(1) 若30°，求PC的长；‎ ‎(2)若点在的延长线上运动，的平分线交于点，你认为∠的大小是否发生变化？若变化，请说明理由；若不变，求出∠的值．‎ C P A B O ‎·‎ 得分 评卷人 ‎24．（本题14分）‎ 如图，在平面直角坐标系中，直角梯形的边落在轴的正半轴上，且∥，，=4，=6，=8．正方形的两边分别落在坐标轴上，且它的面积等于直角梯形面积．将正方形沿轴的正半轴平行移动，设它与直角梯形的重叠部分面积为．‎ ‎（1）分析与计算：‎ 求正方形的边长；‎ ‎（2）操作与求解：‎ ‎①正方形平行移动过程中，通过操作、观察，试判断（＞0）的变化情况是 ；‎ A．逐渐增大 B．逐渐减少 C．先增大后减少 D．先减少后增大 ‎②当正方形顶点移动到点时，求的值；‎ ‎（3）探究与归纳：‎ A B C O D E F 设正方形的顶点向右移动的距离为，求重叠部分面积与的函数关系式．‎ ‎（备用图）‎ A B C 浙江省2007年初中毕业生学业考试（丽水市卷）‎ 数学试卷参考答案 一. 选择题（本题共10小题，每小题4分，共40分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 B A C A B B D A B D 评分标准 选对一题给4分，不选，多选，错选均不给分 二、填空题（本题有6小题，每小题5分，共30分）‎ ‎11．； 12．1；　　　 13．100； 14．4； ‎ ‎15．答案不唯一如：长方体、圆柱等； 16．18．‎ 三、解答题 （本题有8小题，第17～20题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）‎ ‎17．（本题8分）‎ 解：（１）原式＝4－9＋1 ……………………………………………………………………3分 ‎　　　　 ＝－4． …………………………………………………………………………1分 ‎ （2）移项，得 ‎ ＜－1＋7．…………………………………………………………………2分 合并同类项，得 ‎ ＜6． ………………………………………………………………………………2分 ‎18．（本题8分）‎ 证明：∵四边形ABCD为矩形， ‎ ‎∴AC=BD，则BO=CO．………………………………………………………………2分 ‎∵BE⊥AC于E，CF⊥BD于F，‎ ‎ ∴∠BEO=∠CFO=90°．………………………………………………………………2分 又∵∠BOE=∠COF，…………………………………………………………………1分 ‎∴△BOE≌△COF．……………………………………………………………………2分 ‎∴BE=CF．………………………………………………………………………………1分 ‎19．（本题8分）‎ ‎（1）每画一个正确给2分． ………………………………………………………………6分 ‎（2） ；…………………………………………………………1分 ‎＞ ＞ ． ………………………………………………………1分 ‎20．（本题8分）‎ ‎（1）解：∵， ∴．‎ ‎ ∴．‎ ‎ ∴原方程的解是=,=. ………………………………………2分 ‎（2）. ………………………………………………………………………………2分 ‎（3）与或与等. ……………………………………………………………2分 每画出一个正确函数图象给1分. …………………………………………………2分 ‎21．（本题10分）‎ 解：（1）踺子踢到小华处的概率是．………………………………………………………2分 小王 小华 小丽 小丽 小华 小王 小丽 树状图如下：‎ ‎ ‎ ‎…………………………………………3分 列表法如下：‎ 小丽 小王 小华 小王 ‎（小王，小丽）‎ ‎（小王， 小华）‎ 小华 ‎（小华 ，小丽）‎ ‎（小华， 小王）‎ ‎ （2）小王．…………………………………………………………………………………3分 ‎ 理由：若从小王开始踢，三次踢踺后，踺子踢到小王处的概率是，踢到其它两人处的概率都是，因此，踺子踢到小王处的可能性是最小． ……………2分 ‎22．（本题12分）‎ 解：（1）400；…………………………………………………………………………………2分 频数分布图正确． ……………………………………………………………………2分 ‎（2）24．……………………………………………………………………………………3分 ‎（3）设年平均降低的百分率为，‎ ‎ 根据题意，得 ‎ ． ……………………………………………………………………3分 解得：=0.6 , =1.4(舍去) ． ………………………………………………………2分 ‎ 答：年平均降低的百分率是60%.‎ ‎23．（本题12分）‎ 解：（1）连接，‎ ‎ PC是⊙O的切线，‎ ‎∴∠OCP=Rt∠．‎ ‎∵30°，OC==3，‎ ‎∴，即PC=．………………………………………………………5分 ‎（2）∠的大小不发生变化． …………………………………………………………2分 M P C B A O ‎·‎ ‎∵PM是∠CPA的平分线，‎ ‎∴∠CPM=∠MPA．‎ ‎∵OA=OC，∴∠A=∠ACO．‎ 在△APC中，‎ ‎∵∠A＋∠ACP＋∠CPA=180°，‎ ‎∴2∠A＋2∠MPA=90°，∠A＋∠MPA=45°．‎ ‎∴∠CMP=∠A＋∠MPA=45°．………………………………………………………5分 即∠的大小不发生变化．‎ ‎24．（本题14分）‎ ‎ （1）∵，…………2分 ‎ 设正方形的边长为，‎ A B C O D E F M N ‎（如图①）‎ ‎ ∴，或（舍去）．………2分 ‎（2）．………………………………………………2分 ‎ ．…………………3分 ‎（3）①当0≤＜4时，重叠部分为三角形，如图①． ‎ ‎ 可得△∽△，‎ A B C O D E F ‎（如图②）‎ ‎ ∴，=．‎ ‎ ∴．……………………1分 ‎ ‎ ②当4≤＜6时，重叠部分为直角梯形，如图②．‎ ‎ ． ………1分 A B C O D E F M ‎（如图③）‎ ‎ ③当6≤＜8时，重叠部分为五边形，如图③． ‎ ‎ 可得，，．‎ ‎ =．…………………………1分 A O B C D E F M ‎（如图④）‎ ‎ ④当8≤＜10时，重叠部分为五边形，如图④．‎ ‎ =．…………………………1分 ‎⑤当10≤≤14时，重叠部分为矩形，如图⑤．‎ A B C O D E F ‎（如图⑤）‎ ‎．……………1分 ‎(用其它方法求解正确，相应给分)‎ O