20142015中考数学和中点有关的几何综合题20道 11页

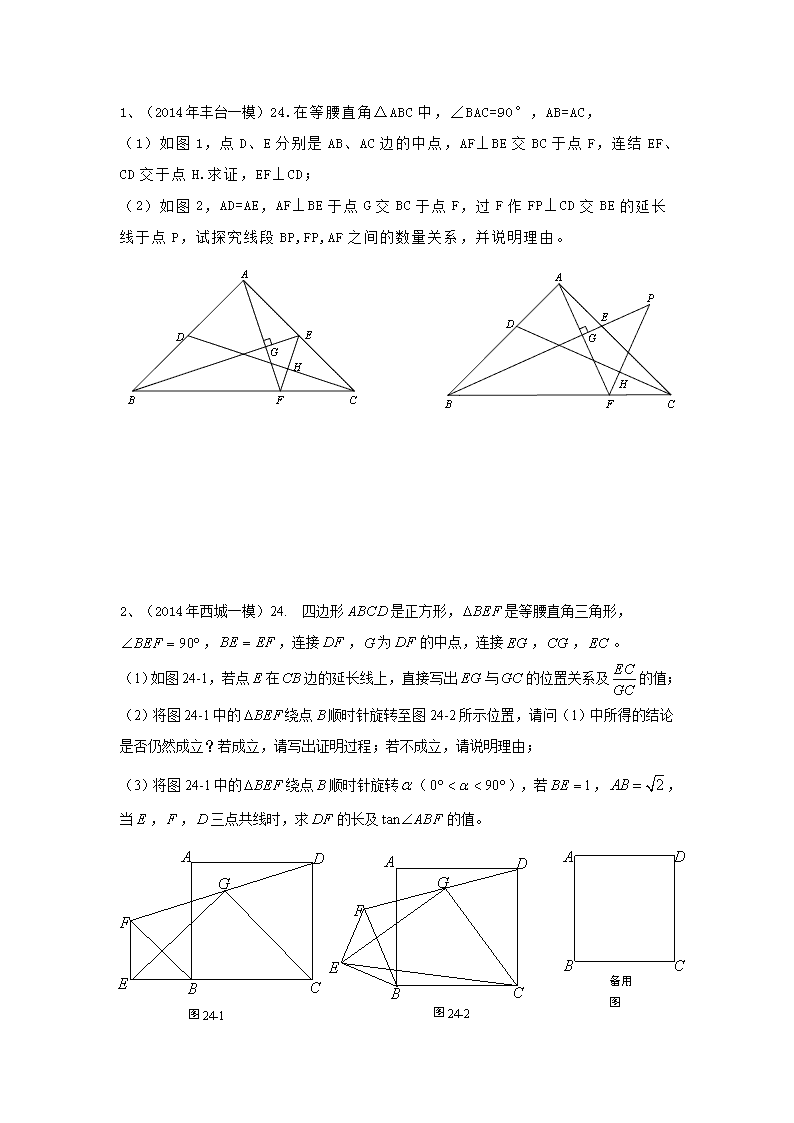
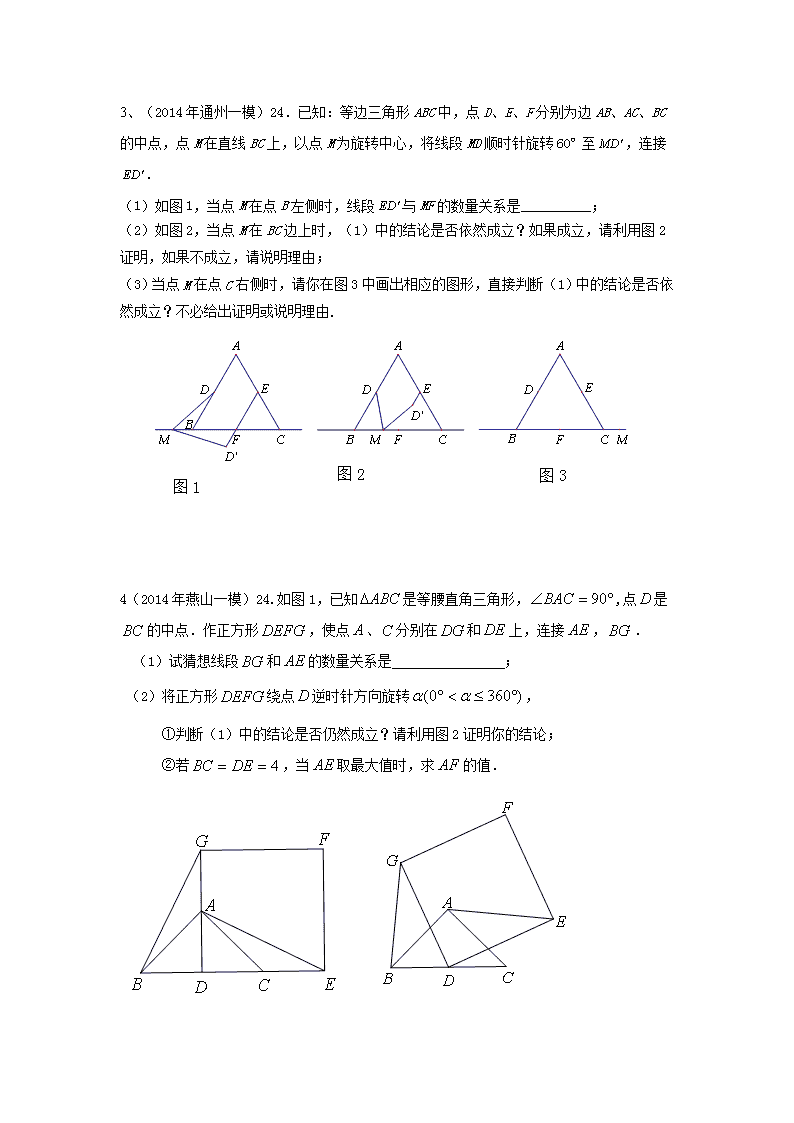
‎1、（2014年丰台一模）24.在等腰直角△ABC中，∠BAC=90°，AB=AC，‎ ‎（1）如图1，点D、E分别是AB、AC边的中点，AF⊥BE交BC于点F，连结EF、CD交于点H.求证，EF⊥CD；‎ ‎（2）如图2，AD=AE，AF⊥BE于点G交BC于点F，过F作FP⊥CD交BE的延长线于点P，试探究线段BP,FP,AF之间的数量关系，并说明理由。‎ ‎2、（2014年西城一模）24. 四边形是正方形，是等腰直角三角形，，，连接，为的中点，连接，，。‎ ‎（1）如图24-1，若点在边的延长线上，直接写出与的位置关系及的值；‎ ‎（2）将图24-1中的绕点顺时针旋转至图24-2所示位置，请问（1）中所得的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；‎ ‎（3）将图24-1中的绕点顺时针旋转（），若，，当，，三点共线时，求的长及的值。‎ A B C D 备用图 A C D G E F B 图24-1‎ 图24-2‎ A C D G E F B ‎3、（2014年通州一模）24．已知：等边三角形ABC中，点D、E、F分别为边AB、AC、BC的中点，点M在直线BC上，以点M为旋转中心，将线段MD顺时针旋转60º至，连接.‎ ‎（1）如图1，当点M在点B左侧时，线段与MF的数量关系是__________；‎ ‎（2）如图2，当点M在BC边上时，（1）中的结论是否依然成立？如果成立，请利用图2证明，如果不成立，请说明理由；‎ 图3‎ ‎（3）当点M在点C右侧时，请你在图3中画出相应的图形，直接判断（1）中的结论是否依然成立？不必给出证明或说明理由.‎ 图2‎ 图1‎ ‎4（2014年燕山一模）24.如图1，已知是等腰直角三角形，,点是的中点．作正方形，使点、分别在和上，连接，．‎ ‎ （1）试猜想线段和的数量关系是 ；‎ ‎ （2）将正方形绕点逆时针方向旋转，‎ ‎ ①判断（1）中的结论是否仍然成立？请利用图2证明你的结论；‎ ‎ ②若，当取最大值时，求的值．‎ ‎ ‎ ‎ ‎ ‎ 图1 图2 ‎ ‎5.（平谷22.） 如图1，若点A、B在直线l同侧，在直线l上找一点P，使AP+BP的值最小，做法是：作点B关于直线l的对称点B′，连接AB′，与直线l的交点就是所求的点P，线段AB′的长度即为AP+BP的最小值．‎ ‎（1）如图2，在等边三角形ABC中，AB=2，点E是AB的中点，AD是高，在AD上找一点P，使BP+PE的值最小．做法是：作点B关于AD的对称点，恰好与点C重合，连接CE交AD于一点，这点就是所求的点P，故BP+PE的最小值为 ；‎ ‎（2）如图3，已知⊙O的直径CD为2，的度数为60°，点B是的中点，在直径CD上作出点P，使BP+AP的值最小，则BP+AP的最小值为 ；‎ ‎（3）如图4，点P是四边形ABCD内一点，BP=m，，分别在边AB、BC上作出点M、N，使的周长最小，求出这个最小值（用含m、的代数式表示）．‎ ‎6.（东城22.）我们曾学过“两点之间线段最短”的知识，常可利用它来解决两条线段和最小的相关问题，下面是大家非常熟悉的一道习题：‎ 如图1，已知，A，B在直线l的同一侧，在l上求作一点，使得PA+PB最小．‎ A B l A B l B′‎ P O 图1‎ 图2‎ 我们只要作点B关于l的对称点B′，（如图2所示）根据对称性可知，PB=PB＇．因此，求AP+BP最小就相当于求AP+PB′最小，显然当A、P、B′在一条直线上时AP+PB′最小，因此连接AB＇，与直线l的交点，就是要求的点P．‎ ‎ 有很多问题都可用类似的方法去思考解决．‎ 探究：‎ A B C D P E 图3‎ ‎（1）如图3，正方形ABCD的边长为2，E为BC的中点， P是BD上 一动点．连结EP，CP，则EP+CP的最小值是_____； ‎ ‎（2）如图4，A是锐角MON内部任意一点，在∠MON的两边OM，ON上各求作一点B，C，组成△ABC，使△ABC周长最小；（不写作法，保留作图痕迹）‎ ‎（3）如图5，平面直角坐标系中有两点A（6，4）、 B（4，6），在y轴上找一点C，在x轴上找一点D，使得四边形ABCD的周长最小，则点C的坐标应该是 ，[点D的坐标应该是 ．‎ O M A N 图4‎ ‎7.（怀柔24．）已知△ABC是等边三角形，E是AC边上一点，F是BC边延长线上一点，且CF=AE，连接BE、EF．‎ ‎（1）如图1，若E是AC边的中点，猜想BE与EF的数量关系为 .‎ ‎（2）如图2，若E是线段AC上的任意一点，其它条件不变，上述线段BE、EF的数量关系是否发生变化，写出你的猜想并加以证明．‎ ‎（3）如图3，若E是线段AC延长线上的任意一点，其它条件不变，上述线段BE、EF的数量关系是否发生变化，写出你的猜想并加以证明．‎ 图3‎ 图111111 111‎ 图2‎ ‎ ‎ ‎8.（密云24．）已知等腰和等腰中，∠ACB=∠AED=90°，且AD=AC ‎（1）发现：如(图1)，当点E在AB上且点C和点D重合时，若点M、N分别是DB、EC的中点，则MN ‎ 与EC的位置关系是 ，MN与EC的数量关系是 ‎ ‎（2）探究：若把（1）小题中的△‎ AED绕点A旋转一定角度，如(图2)所示，连接BD和EC,并连接DB、‎ EC的中点M、N,则MN与EC的位置关系和数量关系仍然能成立吗？若成立，以顺时针旋转45°得到的图形（图3）为例给予证明数量关系成立，若不成立，请说明理由;请以逆时针旋转45°得到的图形（图4）为例给予证明位置关系成立，‎ ‎(2)‎ ‎(图3)‎ ‎(图4)‎ ‎1‎ ‎9.（丰台24.）如图1，在中，，，∠A=30°，点E，F分别是线段BC，AC的中点，连结EF．（1）线段与的位置关系是________， ________．‎ ‎（2）如图2，当绕点顺时针旋转时（），连结AF，BE，（1）中的结论是否仍然成立.如果成立，请证明；如果不成立，请说明理由．‎ ‎（3）如图3，当绕点顺时针旋转时（），延长交于点，如果，求旋转角的度数．‎ 图3‎ 图2‎ 图1‎ ‎10.（燕山24.）如图1，已知是等腰直角三角形，,点是的中点．作正方形，使点、分别在和上，连接，．‎ ‎ （1）试猜想线段和的数量关系是 ；‎ ‎ （2）将正方形绕点逆时针方向旋转，‎ ‎ ①判断（1）中的结论是否仍然成立？请利用图2证明你的结论；‎ ‎ ②若，当取最大值时，求的值．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 图1‎ ‎ 图2 ‎ ‎11.西城一模28.△ABC中，AB=AC．取BC边的中点D，作DE⊥AC于点E，取DE的中点F，连接BE，AF交于点H．‎ ‎ （1）如图1，如果，那么 ， ； ‎ ‎ （2）如图2，如果，猜想的度数和的值，并证明你的结论；‎ ‎ （3）如果，那么 ．（用含的表达式表示）‎ ‎12.丰台一模28．在△ABC中，CA=CB，CD为AB边的中线，点P是线段AC 上任意一点（不与点C重合），过点P作PE交CD于点E，使∠CPE=∠CAB，过点C作CF⊥PE交PE的延长线于点F，交AB于点G.‎ ‎（1）如果∠ACB=90°，‎ ①如图1，当点P与点A重合时，依题意补全图形，并指出与△CDG全等的一个三角形；‎ ②如图2，当点P不与点A重合时，求的值；‎ ‎（2）如果∠CAB=a，如图3，请直接写出的值.（用含a的式子表示）‎ 图2‎ 图1‎ 图3‎ ‎ ‎ ‎13.延庆一模28. 已知，点P是△ABC边AB上一动点（不与A，B重合）分别过点A，B向直线CP作垂线，垂足分别为E，F，Q为边AB的中点.‎ ‎（1）如图1，当点P与点Q重合时，AE与BF的位置关系是 ，QE与QF 的数量关系是 ；‎ ‎（2）如图2，当点P在线段AB上不与点Q重合时，试判断QE与QF的数量关系，‎ 并给予证明；‎ ‎（3）如图3，当点P在线段BA的延长线上时，此时（2）中的结论是否成立？‎ 请画出图形并给予证明. ‎ ‎14.门头沟一模28．在Rt△ABC中，∠ACB=90°，D是AB的中点，DE⊥BC于E，连接CD．‎ ‎（1）如图1，如果∠A=30°，那么DE与CE之间的数量关系是 ．‎ ‎（2）如图2，在（1）的条件下，P是线段CB上一点，连接DP，将线段DP绕点D逆时针旋转60°，得到线段DF，连接BF，请猜想DE、BF、BP三者之间的数量关系，并证明你的结论．‎ ‎（3）如图3，如果∠A=α（0°＜α＜90°），P是射线CB上一动点（不与B、C重合），连接DP，将线段DP绕点D逆时针旋转2α，得到线段DF，连接BF，请直接写出DE、BF、BP三者之间的数量关系（不需证明）．‎ ‎ ‎ 图1 图2 图3‎ ‎15.房山一模28．如图1，已知线段BC=2，点B关于直线AC的对称点是点D，点E为射线CA上一点，且ED=BD，连接DE，BE.‎ (1) 依题意补全图1，并证明：△BDE为等边三角形；‎ (2) 若∠ACB=45°，点C关于直线BD的对称点为点F，连接FD、FB.将△CDE绕点D 顺时针旋转α度（0°＜α＜360°）得到△，点E的对应点为E′，点C的对应点为点C′.‎ ‎①如图2，当α=30°时，连接．证明：=；‎ ‎　　②如图3，点M为DC中点，点P为线段上的任意一点，试探究：在此旋转过程中，线段PM长度的取值范围？‎ 图1‎ 图2‎ 图3‎ ‎16.（2015丰台二模）28． 已知△ABC是锐角三角形，BA=BC，点E为AC边的中点，点D为AB边上一点，且∠ABC=∠AED=α．‎ ‎（1）如图1，当α=40°时，∠ADE= °； ‎ ‎（2） 如图2，取BC边的中点F，联结FD，将∠AED绕点E顺时针旋转适当的角度β(β<α)，得到∠MEN，EM与BA的延长线交于点M， EN与FD的延长线交于点N． ‎ ①依题意补全图形；‎ ②猜想线段EM与EN之间的数量关系，并证明你的结论．‎ 图1 图2‎ ‎17.（2015西城二模）28．正方形ABCD的边长为3，点E，F分别在射线DC，DA上运动，且DE=DF．连接BF，‎ 作EH⊥BF所在直线于点H，连接CH.‎ ‎（1）如图1，若点E是DC的中点，CH与AB之间的数量关系是 ；‎ ‎（2）如图2，当点E在DC边上且不是DC的中点时，（1）中的结论是否成立？若成立 给出证明；若不成立，说明理由；‎ ‎ （3）如图3，当点E，F分别在射线DC，DA上运动时，连接DH，过点D作直线DH的垂线，交直线BF于点K，连接CK，请直接写出线段CK长的最大值．‎ ‎18.（2015房山二模）28.在△ABC中，AB＝BC=2，∠ABC＝90°，BD为斜边AC上的中线，将△ABD绕点D 顺时针旋转α(0°＜α＜180°)得到△EFD，其中点A的对应点为点E，点B的对应点为点F.‎ BE与FC相交于点H.‎ ‎（1）如图1，直接写出BE与FC的数量关系：____________;‎ ‎（2）如图2，M、N分别为EF、BC的中点.求证：MN= ;‎ ‎（3）连接BF，CE，如图3，直接写出在此旋转过程中，线段BF、CE与AC之间的数量关系： .‎ 图1‎ 图2‎ 图3‎ ‎19.（2015石景山二模）28．如图1，点为正方形的中心．‎ ‎（1）将线段绕点逆时针方向旋转，点的对应点为点，连结，，，请依题意补全图1；‎ ‎（2）根据图1中补全的图形，猜想并证明与的关系；‎ ‎（3）如图2，点是中点，△是等腰直角三角形，是的中点，，，，△绕点逆时针方向旋转角度，请直接写出旋转过程中的最大值．‎ ‎ ‎ 图2‎ 图1‎ ‎20（2015怀柔二模）28．在△ABC内侧作射线，自B，C分别向射线AP引垂线，垂足分别为D，E,M为BC边中点，连接MD，ME.‎ ‎（1）依题意补全图1；‎ ‎（2）求证：MD=ME；‎ ‎（3）如图2，若射线AP平分∠BAC，且AC>AB，求证：MD=.‎ 图2‎ 图1‎