中考数学专题复习八 三角形三角形的相似及全等解直角三角形练习 6页

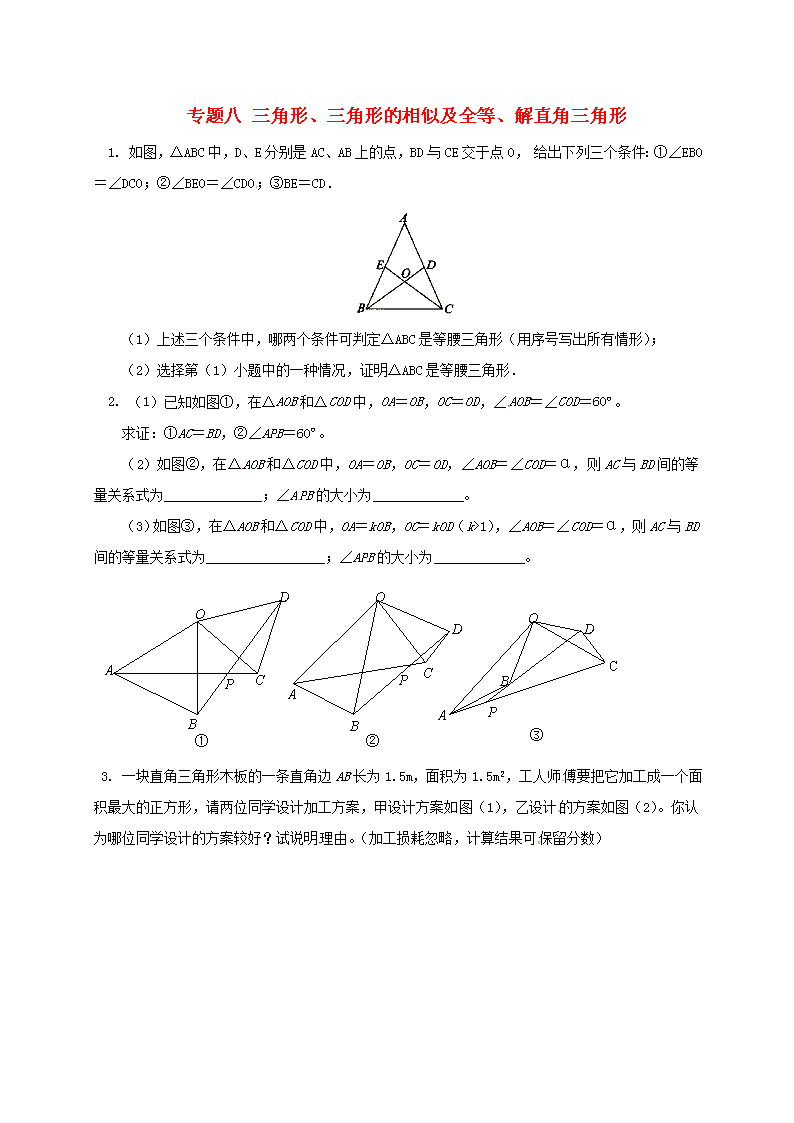
专题八 三角形、三角形的相似及全等、解直角三角形 ‎1. 如图，△ABC中，D、E分别是AC、AB上的点，BD与CE交于点O，给出下列三个条件：①∠EBO＝∠DCO；②∠BEO＝∠CDO；③BE＝CD．‎ ‎（1）上述三个条件中，哪两个条件可判定△ABC是等腰三角形（用序号写出所有情形）； （2）选择第（1）小题中的一种情况，证明△ABC是等腰三角形．‎ ‎2. （1）已知如图①，在△AOB和△COD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝60º。‎ 求证：①AC＝BD，②∠APB＝60º。‎ ‎（2）如图②，在△AOB和△COD中，OA＝OB，OC＝OD，∠AOB＝∠COD＝α，则AC与BD间的等量关系式为______________；∠APB的大小为_____________。‎ ‎（3）如图③，在△AOB和△COD中，OA＝kOB，OC＝kOD（k>1），∠AOB＝∠COD＝α，则AC与BD间的等量关系式为_________________；∠APB的大小为_____________。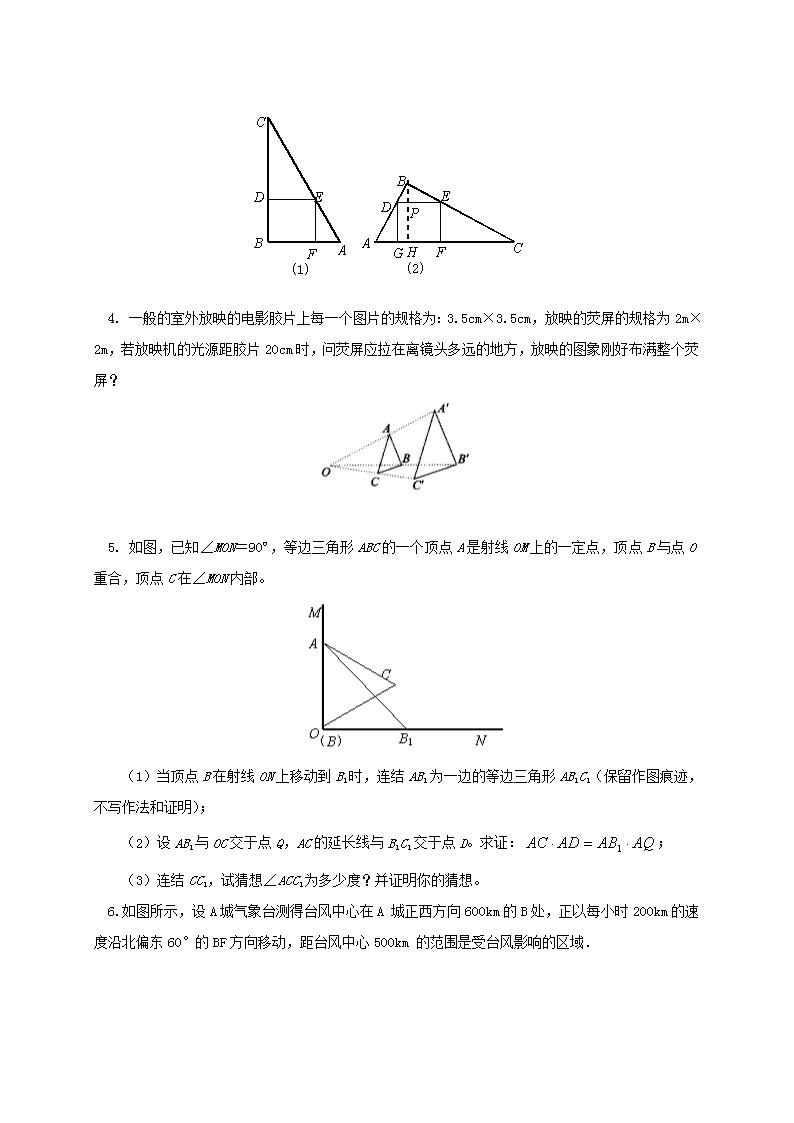‎ ‎ 3. 一块直角三角形木板的一条直角边AB长为‎1.5m，面积为‎1.5m2‎，工人师傅要把它加工成一个面积最大的正方形，请两位同学设计加工方案，甲设计方案如图（1），乙设计的方案如图（2）。你认为哪位同学设计的方案较好？试说明理由。（加工损耗忽略，计算结果可保留分数）‎ ‎4. 一般的室外放映的电影胶片上每一个图片的规格为：‎3.5cm×‎3.5cm，放映的荧屏的规格为‎2m×‎2m，若放映机的光源距胶片‎20cm时，问荧屏应拉在离镜头多远的地方，放映的图象刚好布满整个荧屏？‎ ‎5. 如图，已知∠MON＝90º，等边三角形ABC的一个顶点A是射线OM上的一定点，顶点B与点O重合，顶点C在∠MON内部。‎ ‎（1）当顶点B在射线ON上移动到B1时，连结AB1为一边的等边三角形AB‎1C1（保留作图痕迹，不写作法和证明）； ‎ ‎（2）设AB1与OC交于点Q，AC的延长线与B‎1C1交于点D。求证：；‎ ‎（3）连结CC1，试猜想∠ACC1为多少度？并证明你的猜想。‎ ‎6. 如图所示，设A城气象台测得台风中心在A城正西方向‎600km的B处，正以每小时‎200km的速度沿北偏东60°的BF方向移动，距台风中心‎500km的范围是受台风影响的区域．‎ ‎ （1）A城是否受到这次台风的影响？为什么？‎ ‎（2）若A城受到这次台风的影响，那么A城遭受这次台风的影响有多长时间？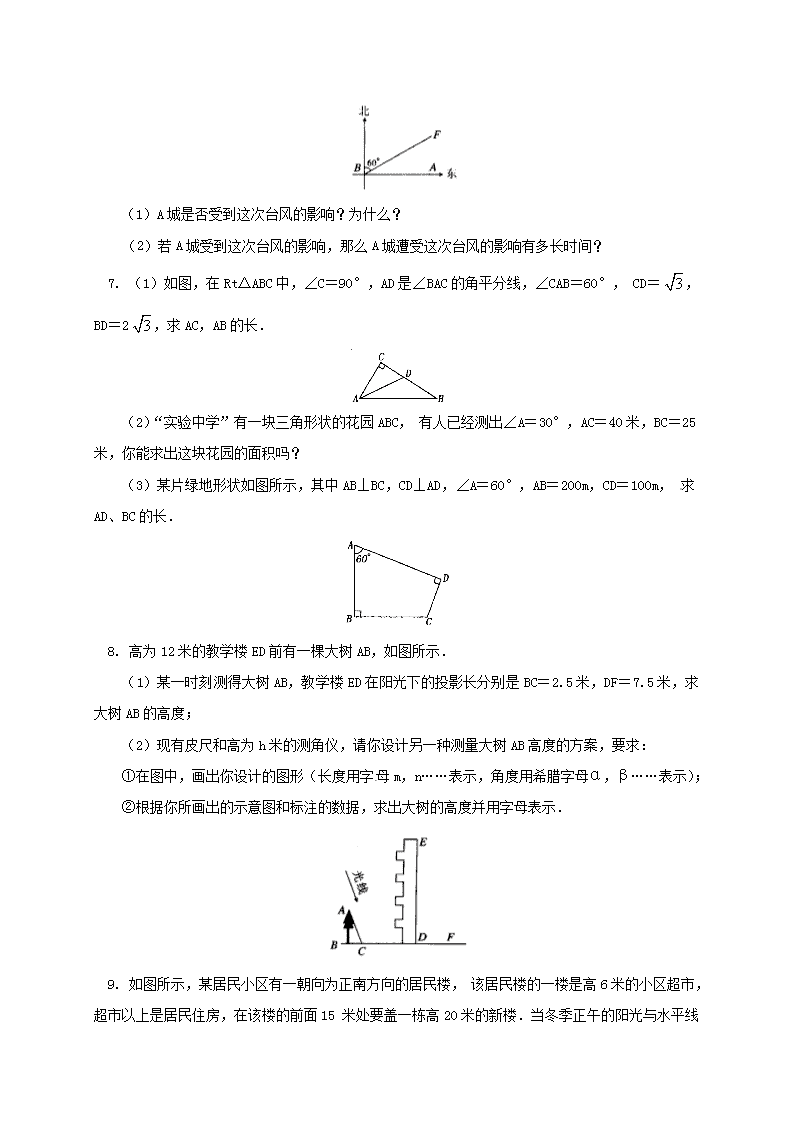‎ ‎7. （1）如图，在Rt△ABC中，∠C＝90°，AD是∠BAC的角平分线，∠CAB＝60°，CD＝，BD＝2，求AC，AB的长．‎ ‎（2）“实验中学”有一块三角形状的花园ABC，有人已经测出∠A＝30°，AC＝‎40米，BC＝25米，你能求出这块花园的面积吗？‎ ‎（3）某片绿地形状如图所示，其中AB⊥BC，CD⊥AD，∠A＝60°，AB＝‎200m，CD＝‎100m，求AD、BC的长．‎ ‎8. 高为‎12米的教学楼ED前有一棵大树AB，如图所示．‎ ‎ （1）某一时刻测得大树AB，教学楼ED在阳光下的投影长分别是BC＝‎2.5米，DF＝‎7.5米，求大树AB的高度；‎ ‎ （2）现有皮尺和高为h米的测角仪，请你设计另一种测量大树AB高度的方案，要求：‎ ‎ ①在图中，画出你设计的图形（长度用字母m，n……表示，角度用希腊字母α，β……表示）；‎ ‎ ②根据你所画出的示意图和标注的数据，求出大树的高度并用字母表示．‎ ‎9. 如图所示，某居民小区有一朝向为正南方向的居民楼，该居民楼的一楼是高‎6米的小区超市，超市以上是居民住房，在该楼的前面15米处要盖一栋高‎20米 的新楼．当冬季正午的阳光与水平线的夹角为32°时．‎ ‎（1）问超市以上的居民住房采光是否受影响，为什么？‎ ‎（2）若要使超市采光不受影响，两楼至少应相距多少米？（结果保留整数，参考数据：sin32°≈，cos32°≈．）‎ 练习答案 ‎1. 解：（1）①③或②③ ‎ ‎（2）已知①③求证△ABC是等腰三角形．‎ 证：先证△EBO≌△DCO．得OB＝OC，得∠DBC＝∠ECB．‎ ‎∴∠ABC＝∠ACB．即△ABC是等腰三角形 ‎2. 证明：∵△AOB和△COD为正三角形，‎ ‎∴OA＝OB，OD＝OC，∠AOB＝60º，∠COD＝60º。‎ ‎∵∠AOB＋∠BOC＝∠COD＋∠BOC，∴∠AOC＝∠BOD。‎ ‎∴△AOC≌△BOD ，∴AC＝BD。∴∠OAC＝∠OBD，‎ ‎∴∠APB＝∠AOB＝60º。‎ ‎（2）AC与BD间的等量关系式为AC＝BD；∠APB的大小为α。‎ ‎（3）AC与BD间的等量关系式为AC＝kBD；∠APB的大小为180º－α。‎ ‎3. 解：方案（1）：有题意可知，DE∥BA，‎ 得△CDE∽△CBA。∴；‎ 方案（2）：作BH⊥AC于H。DE∥AC，得△BDE∽△BAC。‎ ‎∴。∵∴图（1）加工出的正方形面积大。‎ 综上所得，甲同学设计的方案较好。‎ ‎4. 解：胶片上的图象和荧屏上的图象是位似的，镜头就相当于位似中心，因此本题可以转化为位似问题解答．：m ‎5. 解：（1）如图所示；‎ 证明：（2）∵△AOC与△AB‎1C1是等边三角形，‎ ‎∴∠ACB＝∠AB1D＝60º。‎ 又∵∠CAQ＝∠B1AD，∴△ACQ∽△AB1D；‎ ‎（3）猜想∠ACC1＝90º。‎ 证明：∵△AOC和△AB‎1C1为正三角形，AO＝AC，AB1＝AC1，‎ ‎∴∠OAC＝∠C1AB1，‎ ‎∴∠OAC－∠CAQ＝∠C1AB1－∠CAQ，∴∠OAB1＝∠CAC1。∴△AO B1 ≌ △AC C1。‎ ‎∴∠ACC1＝∠AOB1＝90º。‎ ‎6. （1）作AM⊥BF可计算AM＝300km<‎500km，故A城受影响 ‎ ‎（2）受影响时间为小时 ‎7. 解：（1）AC＝3，AB＝6 ‎ ‎（2）能，分两种情况，S△ABC＝200－150和S△ABC＝200＋150 ‎ ‎ ‎ ‎（3）延长BC，AD交于E，AD＝400－100，BC＝200－200．‎ ‎8. 解：连结AC，EF，‎ ‎（1）∵太阳光线是平行的，‎ ‎∴AC∥EF，∠ACB＝∠EFD，‎ ‎∵∠ABC＝∠EDF＝90°，‎ ‎∴△ABC∽△EDF，∴，‎ ‎∴AB＝‎4米 ‎ ‎（2）①如图所示：‎ ‎②AB＝（mtanα＋h）米．‎ ‎9. 解：（1）超市以上居民住房采光受影响，由计算知新楼在居民楼上的投影高约‎11米，‎ 故受影响 ‎ ‎（2）若要使超市采光不受影响，两楼至少相距：＝20×＝32（米） ‎