贺州市2015年中考数学卷 9页

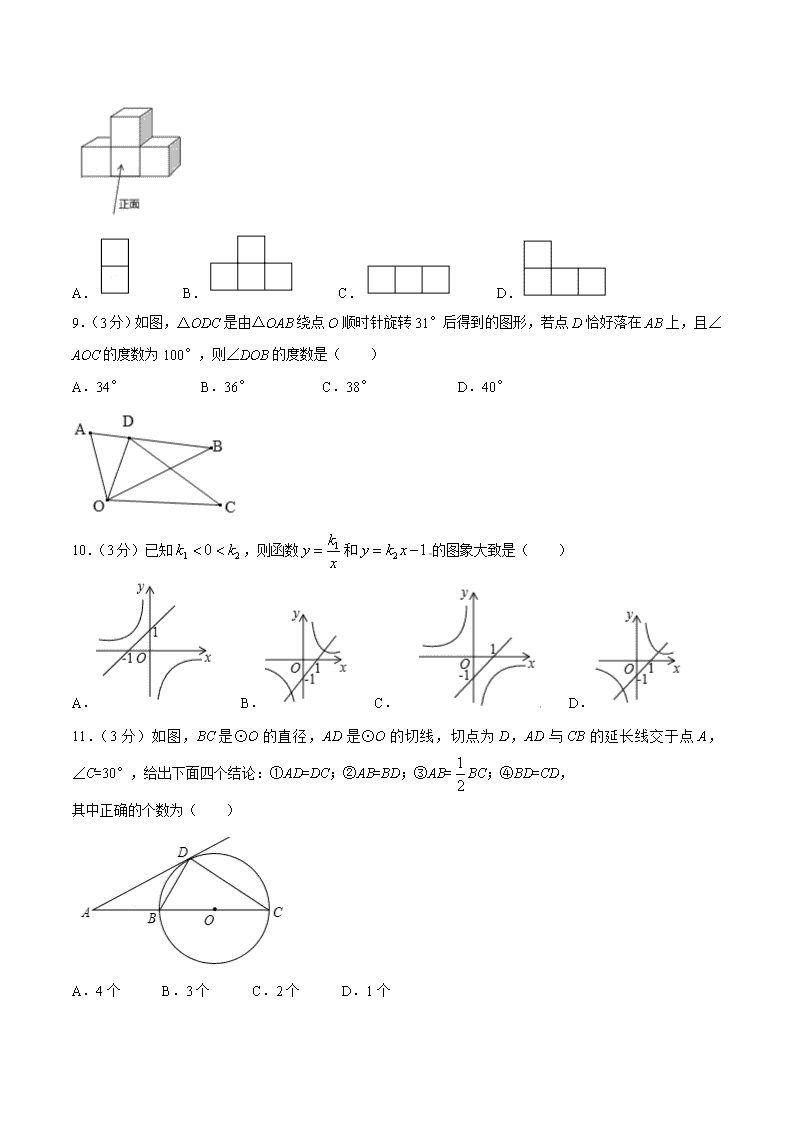
‎2015年广西贺州市中考数学试卷 一、选择题（共12小题，每小题3分，共36分）‎ ‎1．（3分）下列各数是负数的是（　　）‎ A．0 B． C．2.5 D．﹣1‎ ‎2．（3分）如图，下列各组角中，是对顶角的一组是（　　）‎ A．∠1和∠2 B．∠3和∠5 C．∠3和∠4 D．∠1和∠5‎ ‎3．（3分）下列实数是无理数的是（　　）‎ A．5 B．0 C． D．‎ ‎4．（3分）下面的图形中，既是轴对称图形又是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎5．（3分）一组数据3，2，x，1，2的平均数是2，则这组数据的中位数和众数分别是（　　）‎ A．3，2 B．2，1 C．2，2.5 D．2，2‎ ‎6．（3分）下列运算正确的是（　　）‎ A． B． C． D．‎ ‎7．（3分）把多项式分解因式的结果是（　　）‎ A． B．‎ C． D．‎ ‎8．（3分）如图是由四个小正方体叠成的一个几何体，它的左视图是（　　）‎ A． B． C． D．‎ ‎9．（3分）如图，△ODC是由△OAB绕点O顺时针旋转31°后得到的图形，若点D恰好落在AB上，且∠AOC的度数为100°，则∠DOB的度数是（　　）‎ A．34° B．36° C．38° D．40°‎ ‎10．（3分）已知，则函数和的图象大致是（　　）‎ A． B． C． D．‎ ‎11．（3分）如图，BC是⊙O的直径，AD是⊙O的切线，切点为D，AD与CB的延长线交于点A，∠C=30°，给出下面四个结论：①AD=DC；②AB=BD；③AB=BC；④BD=CD，‎ 其中正确的个数为（　　）‎ A．4个 B．3个 C．2个 D．1个 ‎12．（3分）观察下列等式：21=2，22=4，23=8，24=16，25=32，26=64，27=128，…，解答下面问题：2+22+23+24+…+22015﹣1的末位数字是（　　）‎ A．0 B．3 C．4 D．8‎ 二、填空题（共6小题，每小题3分，共18分）‎ ‎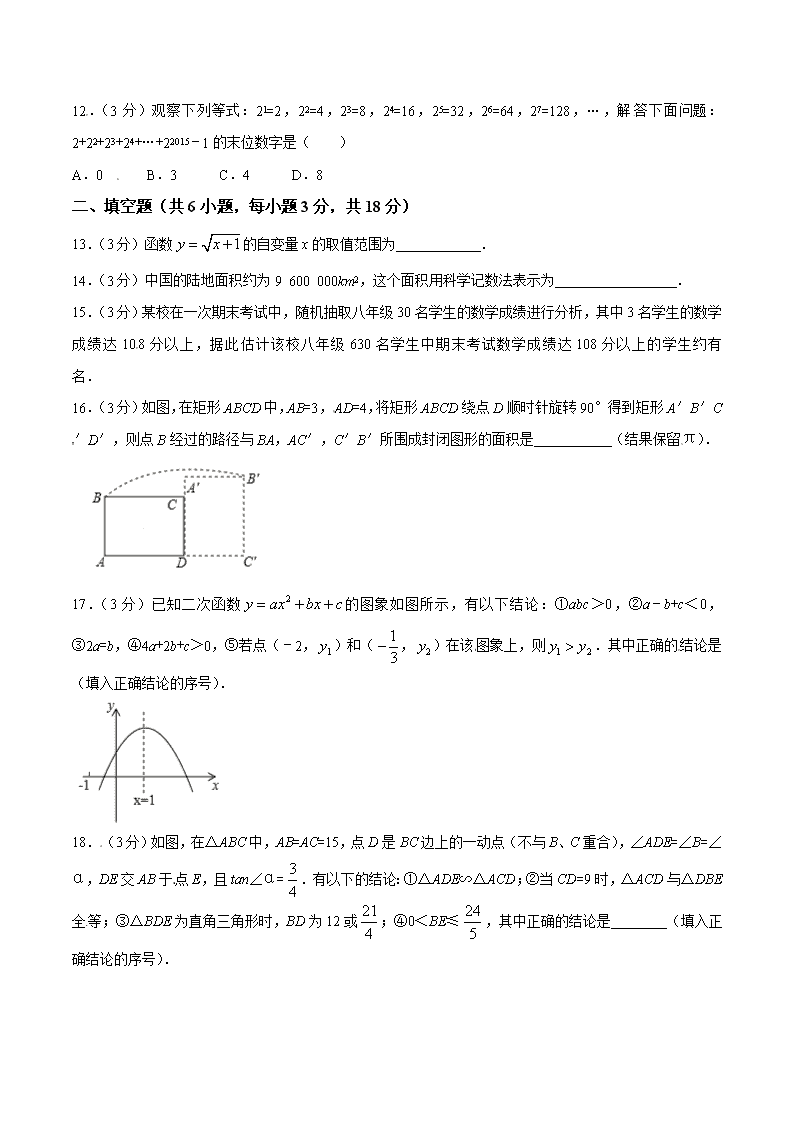13．（3分）函数的自变量x的取值范围为 ．‎ ‎14．（3分）中国的陆地面积约为9 600 000km2，这个面积用科学记数法表示为 ．‎ ‎15．（3分）某校在一次期末考试中，随机抽取八年级30名学生的数学成绩进行分析，其中3名学生的数学成绩达108分以上，据此估计该校八年级630名学生中期末考试数学成绩达108分以上的学生约有 名．‎ ‎16．（3分）如图，在矩形ABCD中，AB=3，AD=4，将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′，则点B经过的路径与BA，AC′，C′B′所围成封闭图形的面积是 （结果保留π）．‎ ‎17．（3分）已知二次函数的图象如图所示，有以下结论：①abc＞0，②a﹣b+c＜0，③2a=b，④4a+2b+c＞0，⑤若点（﹣2，）和（，）在该图象上，则．其中正确的结论是 （填入正确结论的序号）．‎ ‎18．（3分）如图，在△ABC中，AB=AC=15，点D是BC边上的一动点（不与B、C重合），∠ADE=∠B=∠α，DE交AB于点E，且tan∠α=．有以下的结论：①△ADE∽△ACD；②当CD=9时，△ACD与△DBE全等；③△BDE为直角三角形时，BD为12或；④0＜BE≤，其中正确的结论是 （填入正确结论的序号）．‎ 三、解答题（共8小题，满分66分）‎ ‎19．（6分）计算：．‎ ‎20．（6分）解分式方程：．‎ ‎21．（8分）在甲口袋中有三张完全相同的卡片，分别标有﹣1，1，2，乙口袋中有完全相同的卡片，分别标有﹣2，3，4，从这两个口袋中各随机取出一张卡片．‎ ‎（1）用树状图或列表表示所有可能出现的结果；‎ ‎（2）求两次取出卡片的数字之积为正数的概率．‎ ‎22．（8分）根据道路管理规定，在贺州某段笔直公路上行驶的车辆，限速40千米/时，已知交警测速点M到该公路A点的距离为米，∠MAB=45°，∠MBA=30°（如图所示），现有一辆汽车由A往B方向匀速行驶，测得此车从A点行驶到B点所用的时间为3秒．‎ ‎（1）求测速点M到该公路的距离；‎ ‎（2）通过计算判断此车是否超速．（参考数据：≈1.41，≈1.73，≈2.24）‎ ‎23．（8分）如图，将矩形ABCD沿对角线BD对折，点C落在E处，BE与AD相交于点F．若DE=4，BD=8．‎ ‎（1）求证：AF=EF；‎ ‎（2）求证：BF平分∠ABD．‎ ‎24．（8分）某商场销售一批同型号的彩电，第一个月售出50台，为了减少库存，第二个月每台降价500元将这批彩电全部售出，已知第一个月的销售额与第二个月的销售额相等，这两个月销售总额超过40万元．‎ ‎（1）求第一个月每台彩电销售价格；‎ ‎（2）这批彩电最少有多少台？‎ ‎25．（10分）如图，AB是⊙O的直径，C为⊙O上一点，AC平分∠BAD，AD⊥DC，垂足为D，OE⊥AC，垂足为E．‎ ‎（1）求证：DC是⊙O的切线；‎ ‎（2）若OE=cm，AC=cm，求DC的长（结果保留根号）．‎ ‎26．（12分）如图，已知抛物线与直线AB相交于A（﹣3，0），B（0，3）两点．‎ ‎（1）求这条抛物线的解析式；‎ ‎（2）设C是抛物线对称轴上的一动点，求使∠CBA=90°的点C的坐标；‎ ‎（3）探究在抛物线上是否存在点P，使得△APB的面积等于3？若存在，求出点P的坐标；若不存在，请说明理由．‎