中考预测模拟题 12页

‎2013年临沂市初中学生学业考试 数 学 模拟题 一、选择题（本题共14小题，每小题3分，共42分）在每小题所给的四个选项中，只有一项是符合题目要求的.‎ ‎1. 在与之间加上如下运算符号，其结果最大的是【     】‎ A．＋           B．－           C．×            D．÷  ‎ ‎2. 吸烟有害健康．据中央电视台‎2013年3月30日报道，全世界每因吸烟引起的疾病致死的人数大约为600万，数据600万用科学记数法表示为【     】 ‎ A．0.6×107      B．6×106      C．60×105      D．6×105‎ ‎3. 下列运算正确的是【 】‎ A．x4•x3=x12 B．（x3）4=x‎81 C．x4÷x3=x（x≠0） D．x4+x3=x7‎ ‎4. 已知：如图，BD平分∠ABC，点E在BC上，EF∥AB．若∠CEF=100°，则∠ABD的度数为【 】‎ ‎（　　）‎ A．60°　　B．50°　　C．40°　　D．30°‎ ‎5.由方程组可得出x与y的关系是【 】‎ A． B． C． D．‎ ‎6. 班主任王老师将6份奖品放在6个完全相同的不透明礼盒中，准备将他们奖给小英等6位获“爱集体标兵”称号的同学。这些奖品中3份是学习文具，2份是科普读物，1份是科技馆通票。小英同学从中随机取一份奖品，恰好取到科普读物的概率是【 】‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎7. 不等式组的解集是【 】‎ A． x＞﹣3 B． x＜﹣3 C． x＞2 D． x＜2‎ ‎ ‎ ‎8. 某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量，如下表所示：‎ ‎ 用电量（度）‎ ‎120‎ ‎140‎ ‎160‎ ‎180‎ ‎200‎ 户数 ‎2‎ ‎3‎ ‎6‎ ‎7‎ ‎2‎ 则这20户家庭该月用电量的纵数和中位数分别是【 】‎ Ａ．180,160 Ｂ．160,180 Ｃ．160，160 Ｄ．180,180‎ ‎9. 在平面直角坐标系中，△ABC的三个顶点坐标分别为A(4，5)，B(1，2)，C(4，2)，将△ABC向左平移5个单位后，A的对应点A1的坐标是【 】‎ A． (0，5) B． (－1，5) C．(9，5) D．(－1，0)‎ ‎10. 如图，水平放置的圆柱体的三视图是【 】‎ A． B．‎ C． D．‎ ‎11.临沂市某景点门票价格：成人票每张70元，儿童票每张35元.小明买20张门票共花了1225元,设其中有张成人票，张儿童票，根据题意，下列方程组正确的是【 】‎ A. B. C. D.‎ ‎ 12.已知二次函数的图象如图所示对称轴为．下列结论中，正确的是【 】‎ ‎ ‎ ‎ ‎ A． B． C． D．‎ ‎13. 已知关于x的一元二次方程（a﹣l）x2﹣2x+l=0有两个不相等的实数根，则a的取值范围是【 】‎ A．a＞2 B．a＜2 C． a＜2且a≠l D． a＜﹣2‎ ‎14. 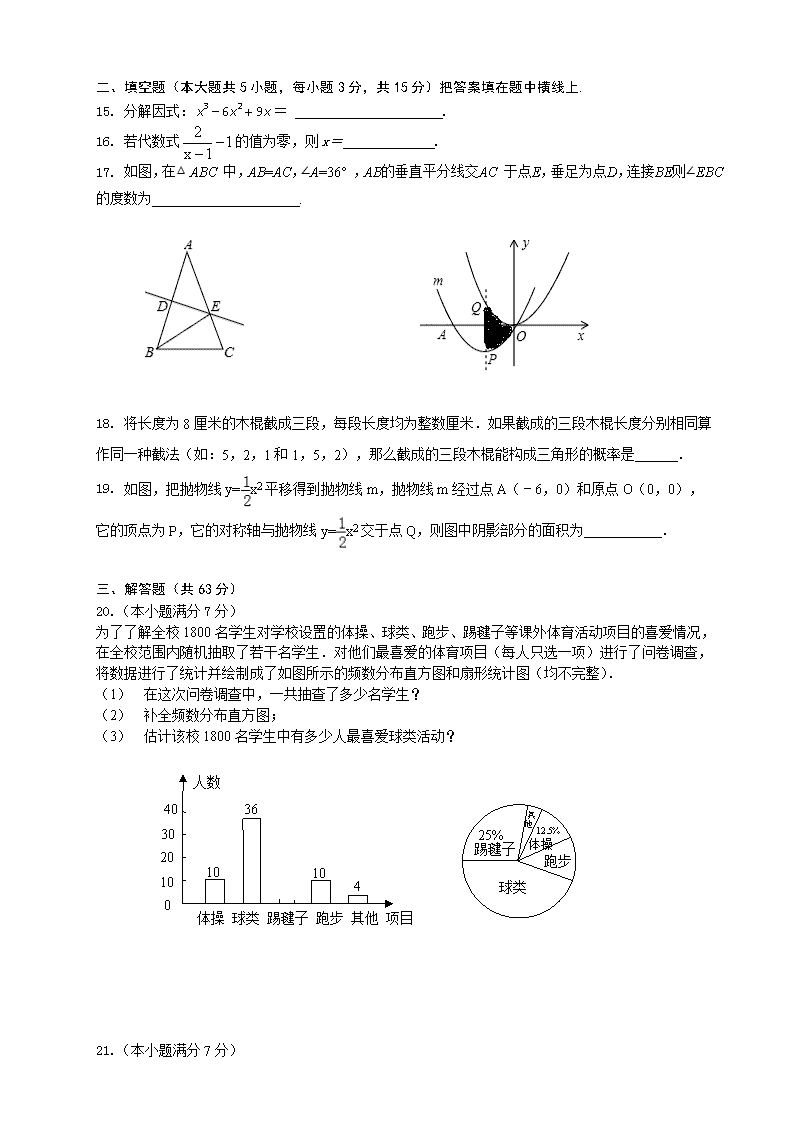如图，在Rt△ABC中，∠C=90°，AC=BC=‎6cm，点P 从点A 出发，沿AB方向以每秒cm的速度向终点B运动；同时，动点Q从点B出发沿BC方向以每秒‎1cm 的速度向终点C 运动，将△PQC沿BC翻折，点P的对应点为点P′.设Q点运动的时间t秒，若四边形QPCP′为菱形，则t的值为【 】‎ A． B．2 C． D． 4 ‎ 二、填空题（本大题共5小题，每小题3分，共15分）把答案填在题中横线上.‎ ‎15. 分解因式：＝ .‎ ‎16. 若代数式的值为零，则x＝ .‎ ‎17. 如图，在△ ABC 中，AB=AC，∠A=36° ，AB的垂直平分线交AC 于点E，垂足为点D，连接BE则∠EBC 的度数为 .‎ ‎ ‎ ‎18. 将长度为8厘米的木棍截成三段，每段长度均为整数厘米．如果截成的三段木棍长度分别相同算作同一种截法（如：5，2，1和1，5，2），那么截成的三段木棍能构成三角形的概率是 ．‎ ‎19. 如图，把抛物线y=x2平移得到抛物线m，抛物线m经过点A（﹣6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线y=x2交于点Q，则图中阴影部分的面积为　 　．‎ 三、解答题（共63分）‎ ‎20.（本小题满分7分）‎ 为了了解全校1800名学生对学校设置的体操、球类、跑步、踢毽子等课外体育活动项目的喜爱情况，在全校范围内随机抽取了若干名学生．对他们最喜爱的体育项目（每人只选一项）进行了问卷调查，将数据进行了统计并绘制成了如图所示的频数分布直方图和扇形统计图（均不完整）．‎ （1） 在这次问卷调查中，一共抽查了多少名学生？‎ （2） 补全频数分布直方图；‎ （3） 估计该校1800名学生中有多少人最喜爱球类活动？‎ 体操 球类 踢毽子 跑步 其他 项目 人数 ‎40‎ ‎0‎ ‎20‎ ‎10‎ ‎30‎ ‎10‎ ‎36‎ ‎10‎ ‎4‎ 踢毽子 ‎25%‎ 球类 跑步 ‎12.5%‎ 体操 其 他 ‎21.（本小题满分7分）‎ 某学校后勤人员到一家文具店给九年级的同学购买考试用文具包，文具店规定一次购买400个以上，可享受8折优惠.若给九年级学生每人购买一个，不能享受8折优惠，需付款1936元；若多买88个，就可享受8折优惠，同样只需付款1936元.请问该学校九年级学生有多少人？‎ ‎22.（本小题满分7分））‎ 如图，△ABC中，∠B=90°，AB=‎6cm，BC=‎8cm，将△ABC沿射线BC方向平移‎10cm，得到△DEF，A，B，C的对应点分别是D,E,F，连结AD，求证：四边形ACFD是菱形。‎ ‎23.（本小题满分9分）‎ 如图，△ABC中，∠ACB=90°，D是边AB上的一点，且∠A=2∠DCB.E是BC上的一点，以EC为直径的⊙O经过点D。‎ ‎（1）求证:AB是⊙O的切线；‎ ‎（2）若CD的弦心距为1,BE=EO.求BD的长. ‎ ‎24.（本小题满分9分）‎ 已知：如图，在平面直角坐标系中，一次函数的图象与反比例函数的图象交于一、三象限内的A．B两点，与x轴交于C点，点A的坐标为（2,m)，点B的坐标为（n，－2），tan∠BOC＝。‎ ‎（l）求该反比例函数和一次函数的解析式；‎ ‎（2）在x轴上有一点E（O点除外），使得△BCE与△BCO的面积相等，求出点E的坐标．‎ ‎25.（本小题满分11分）‎ 在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），∠BPE＝，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G． ‎ ‎（1） 当点P与点C重合时（如图①）．求证：△BOG≌△POE；（4分） ‎ ‎（2）通过观察、测量、猜想：BF:PE=______________，并结合图②证明你的猜想；（5分） ‎ ‎（3）把正方形ABCD改为菱形，其他条件不变（如图③），若∠ACB=α,求的值．（用含α的式子表示）‎ ‎26.（本小题满分13分）‎ 如图，已知抛物线y＝ax2＋bx＋c(a≠0)的对称轴为x＝1，且抛物线经过A（—1，0）、C（0，—‎ ‎3）两点，与x轴交于另一点B．‎ ‎（1）求这条抛物线所对应的函数关系式；‎ ‎（2）在抛物线的对称轴x＝1上求一点M，使点M到点A的距离与到点C的距离之和最小，并求出此时点M的坐标；‎ ‎（3）设点P为抛物线的对称轴x＝1上的一动点，求使∠PCB＝90°的点P的坐标．‎ x y O x＝1‎ 第26题 A C B ‎ ‎ ‎2013年临沂市初中学生学业考试样卷 数学参考答案 一、选择题（每小题3分，共42分）‎ ‎1.A 2.B 3.C 4.B 5.A 6.B 7.C 8.A 9.B 10. A 11.B 12.D 13.C 14.B 二、填空题（每小题3分，共15分）‎ ‎15. 16.3 17. 36° 18. 19. ‎ 三、解答题（共63分）‎ ‎20．解：（1）（人）．‎ 一共抽查了80人． （2分）‎ ‎（2）（人），‎ 图形补充正确． （4分）‎ ‎（3）（人）．‎ 估计全校有810人最喜欢球类活动． （7分）‎ ‎ ‎ ‎21. 解：设九年级学生有x人，根据题意，列方程得： ……………1分 ‎ ×0.8=, …………………3分 整理得0.8（x+88）=x，‎ 解之得x=352, ……………………5分 ‎ 经检验x=352是原方程的解. ……………………6分 答：这个学校九年级学生有352人. ……………………7分 ‎ ‎ ‎22. 证明：由平移变换的性质得，CF=AD=10，DF=AC。 ……………………2分 ‎∵∠B=90°，AB=6，BC=8，‎ ‎∴。 ……………………4分 ‎∴AC=DF=AD=CF=10。 ……………………6分 ‎∴四边形ACFD是菱形。 ……………………7分 ‎23. （1）证明：如图，连接OD， ‎ ‎∵OD=OC，∴∠DCB=∠ODC。‎ 又∵∠DOB和∠DCB为弧DE所对的圆心角和圆周角，‎ ‎∴∠DOB =2∠DCB。‎ 又∵∠A=2∠DCB，∴∠A=∠DOB。‎ ‎∵∠ACB=90°，∴∠A+∠B=90°。‎ ‎∴∠DOB+∠B=90°。∴∠BDO=90°。∴OD⊥AB。‎ ‎∴AB是⊙O的切线。……………………4分 ‎（2）如图，过点O作OM⊥CD于点M，‎ ‎∵OD=OE=BE=BO，∠BDO=90°，∴∠B=30°。∴∠DOB=60°。‎ ‎∵OD=OC，∴∠DCB=∠ODC。‎ 又∵∠DOB和∠DCB为弧DE所对的圆心角和圆周角，∴∠DOB =2∠DCB。‎ ‎∴∠DCB=30°。‎ ‎∵在Rt△OCM中，∠DCB=30°，OM=1，∴OC=2OM=2。‎ ‎∴OD=2，BO=BE+OE=2OE=4。‎ ‎∴在Rt△BDO中，根据勾股定理得：‎ ‎。 ……………………9分 ‎24.解：解：（1）过B点作BD⊥x轴，垂足为D，‎ ‎∵B（n，﹣2），∴BD=2，‎ 在Rt△OBD在，tan∠BOC=，即=，解得OD=5，‎ 又∵B点在第三象限，∴B（﹣5，﹣2），‎ 将B（﹣5，﹣2）代入y=中，得k=xy=10，‎ ‎∴反比例函数解析式为y=，‎ 将A（2，m）代入y=中，得m=5，∴A（2，5），‎ 将A（2，5），B（﹣5，﹣2）代入y=ax+b中，‎ 得，解得，‎ 则一次函数解析式为y=x+3； ……………………5分 ‎（2）由y=x+3得C（﹣3，0），即OC=3，‎ ‎∵S△BCE=S△BCO，‎ ‎∴CE=OC=3，‎ ‎∴OE=6，即E（﹣6，0）． ……………………9分 ‎ ‎ ‎25. （1）证明：∵四边形ABCD是正方形，P与C重合， ‎ ‎∴OB=OP ， ∠BOC=∠BOG=90°。 ‎ ‎∵PF⊥BG ，∠PFB=90°，∴∠GBO=90°—∠BGO，∠EPO=90°—∠BGO。 ∴∠GBO=∠EPO 。∴△BOG≌△POE（AAS）。‎ ‎（2）BF:PE=证明如下： ‎ 如图，过P作PM//AC交BG于M，交BO于N， ∴∠PNE=∠BOC=900， ∠BPN=∠OCB。‎ ‎ ∵∠OBC=∠OCB =450，  ∴ ∠NBP=∠NPB。 ∴NB=NP。 ‎ ‎∵∠MBN=900—∠BMN，  ∠NPE=900—∠BMN，‎ ‎∴∠MBN=∠NPE。‎ ‎ ∴△BMN≌△PEN（ASA）。∴BM=PE。‎ ‎ ∵∠BPE=∠ACB，∠BPN=∠ACB，∴∠BPF=∠MPF。 ‎ ‎∵PF⊥BM，∴∠BFP=∠MFP=900。 ‎ 又∵PF=PF， ∴△BPF≌△MPF（ASA）。‎ ‎∴BF=MF ，即BF=BM。 ‎ ‎∴BF=PE， 即BF:PE=‎ ‎（3）如图，过P作PM//AC交BG于点M，交BO于点N， ‎ ‎∴∠BPN=∠ACB=α，∠PNE=∠BOC=900。 ‎ 由（2）同理可得BF=BM， ∠MBN=∠EPN。  ‎ ‎∵∠BNM=∠PNE=900，‎ ‎∴△BMN∽△PEN。 ‎ Rt△BNP中，，  ‎ ‎∴‎ 即 ‎∴‎ ‎26.解：方法一： ⑴设抛物线的解析式为y ＝ax2＋bx＋c ，则有：‎ 解得：，所以抛物线的解析式为y ＝x2－2x－3.‎ 方法二：设抛物线的解析式为，则有：‎ 解得：，所以抛物线的解析式为即y ＝x2－2x－3.‎ ‎⑵令x2－2x－3＝0，解得x1＝－１，x2＝3,所以B点坐标为（3，0）.‎ 设直线BC的解析式为y ＝kx＋b,‎ 则，解得，所以直线解析式是y ＝x－3.‎ 当x＝1时，y＝－2.所以M点的坐标为（1，－2）.‎ ‎⑶方法一：要使∠PBC＝90°，则直线PC过点C，且与BC垂直，‎ 又直线BC的解析式为y ＝x－3，‎ 所以直线PC的解析式为y ＝－x－3，当x＝1时，y＝－4，‎ 所以P点坐标为（1，－4）.‎ 方法二：设P点坐标为（1，y），则PC2＝12＋（－3－y）2,BC2＝32＋32；PB2＝22＋y2‎ 由∠PBC＝90°可知△PBC是直角三角形，且PB为斜边，则有PC2＋BC2＝PB2.‎ 所以：[12＋（－3－y）2]＋[32＋32]＝22＋y2；解得y ＝－4，‎ 所以P点坐标为（1，－4）.‎ 备用：‎ ‎26. 如图，已知抛物线与一直线相交于A（﹣‎ ‎1，0），C（2，3）两点，与y轴交于点N．其顶点为D． ‎ ‎（1）抛物线及直线AC的函数关系式； ‎ ‎（2）设点M（3，m），求使MN+MD的值最小时m的值； ‎ ‎（3）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值 ‎ ‎ 解：（1）由抛物线y=﹣x2+bx+c过点A（﹣1，0）及C（2，3）得，‎ ‎，‎ 解得，‎ 故抛物线为y=﹣x2+2x+3‎ 又设直线为y=kx+n过点A（﹣1，0）及C（2，3）得 ‎，‎ 解得 故直线AC为y=x+1；‎ ‎（2）作N点关于直线x=3的对称点N′，则N′（6， 3），由（1）得D（1，4），‎ 故直线DN′的函数关系式为y=﹣x+，‎ 当M（3，m）在直线DN′上时，MN+MD的值最小，‎ 则m=﹣×=；‎ ‎（3）方法一：过点P作PQ⊥x轴交AC于点Q；过点C作CG⊥x轴于点G，如图1‎ 设Q（x，x+1），则P（x，﹣x2+2x+3）‎ ‎∴PQ=（﹣x2+2x+3）﹣（x﹣1）‎ ‎=﹣x2+x+2‎ 又∵S△APC=S△APQ+S△CPQ=PQ•AG ‎=（﹣x2+x+2）×3‎ ‎=﹣（x﹣）2+‎ ‎∴面积的最大值为．‎ 方法二：过点P作PQ⊥x轴交AC于点Q，交x轴于点H；过点C作CG⊥x轴于点G，如图2，‎ 设Q（x，x+1），则P（x，﹣x2+2x+3）‎ 又∵S△APC=S△APH+S直角梯形PHGC﹣S△AGC=（x+1）（﹣x2+2x+3）+（﹣x2+2x+3+3）（2﹣x）﹣×3×3‎ ‎=﹣x2+x+3‎ ‎=﹣（x﹣）2+‎ ‎∴△APC的面积的最大值为．‎