中考二次函数压轴题及答案 24页

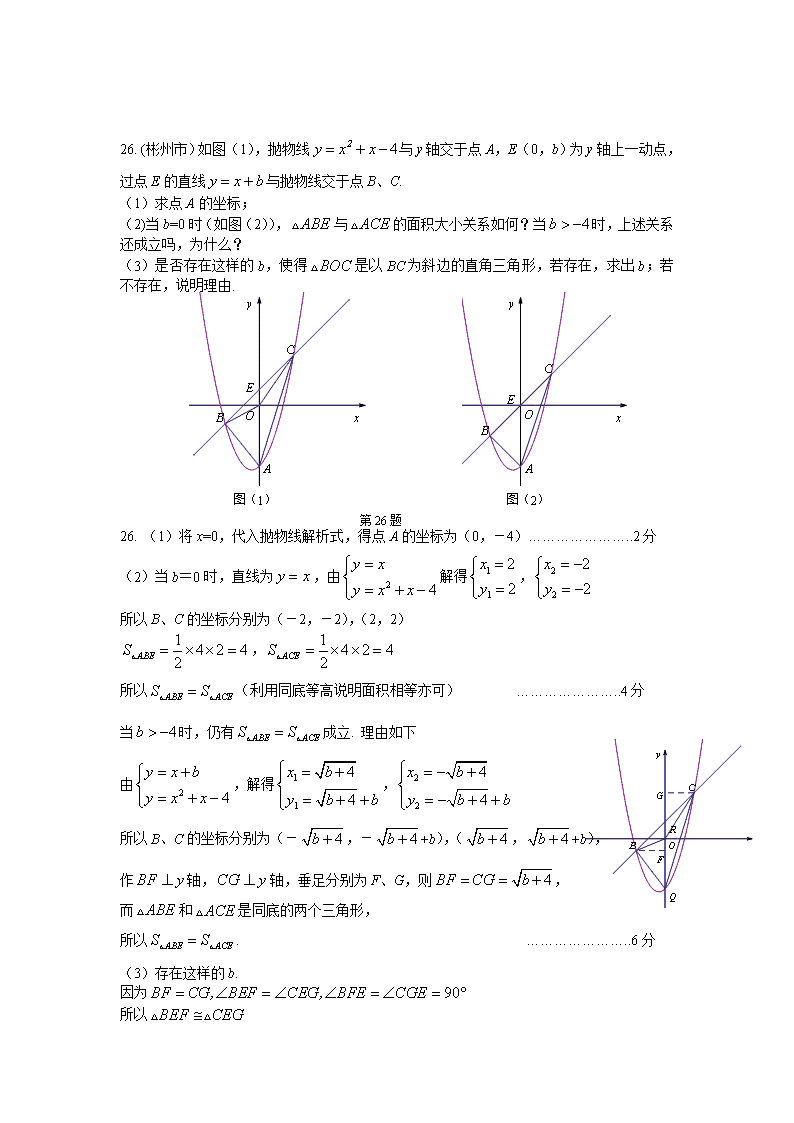
‎26. (彬州市）如图（1），抛物线与y轴交于点A，E（0，b）为y轴上一动点，过点E的直线与抛物线交于点B、C.‎ ‎（1）求点A的坐标；‎ ‎（2)当b=0时（如图（2）），与的面积大小关系如何？当时，上述关系还成立吗，为什么？‎ 第26题 图（1）‎ 图（2）‎ ‎（3）是否存在这样的b，使得是以BC为斜边的直角三角形，若存在，求出b；若不存在，说明理由. ‎ ‎26. （1）将x=0，代入抛物线解析式，得点A的坐标为（0，－4）…………………..2分 ‎（2）当b＝0时，直线为，由解得， ‎ 所以B、C的坐标分别为（－2，－2），（2，2） ‎ ‎，‎ 所以（利用同底等高说明面积相等亦可） …………………..4分 当时，仍有成立. 理由如下 由，解得， ‎ 所以B、C的坐标分别为（－，－+b），（，+b），‎ 作轴，轴，垂足分别为F、G，则，‎ 而和是同底的两个三角形，‎ 所以. …………………..6分 ‎（3）存在这样的b.‎ 因为 所以 所以，即E为BC的中点 所以当OE=CE时，为直角三角形 …………………..8分 因为 所以 ，而 所以，解得，‎ 所以当b＝4或－2时，ΔOBC为直角三角形. ………………….10分 ‎ 25. ‎(常德）如图9，已知抛物线轴交于点A（-4，0）和B（1，0）两点，与y轴交于C点.‎ (1) 求此抛物线的解析式；‎ (2) 设E是线段AB上的动点，作EF∥AC交BC于F，连接CE，当的面积是面积的2倍时，求E点的坐标；‎ (3) 若P为抛物线上A、C两点间的一个动点，过P作y轴的平行线，交AC于Q，当P点运动到什么位置时，线段PQ的值最大，并求此时P点的坐标.‎ A B O C 图9‎ y x ‎25．解：（1）由二次函数与轴交于、两点可得：‎ ‎　　　　　　　　　　解得：　‎ ‎　　　　　　故所求二次函数的解析式为． ………………3分 ‎（2）∵S△CEF=2 S△BEF, ∴ ………………4分 ‎ ∵EF//AC, ∴,‎ ‎ ∴△BEF～△BAC, ………………5分 ‎∴得 ………………6分 故E点的坐标为(,0). ………………7分 ‎　　　（3）解法一：由抛物线与轴的交点为，则点的坐标为（0，－2）．若设直线的解析式为，则有　解得： ‎ 故直线的解析式为． ………………8分 若设点的坐标为，又点是过点所作轴的平行线与直线的交点，则点的坐标为（．则有：‎ ‎　　　　　　　＝‎ ‎＝‎ 即当时，线段取大值，此时点的坐标为（－2，－3）………10分 解法二：延长交轴于点，则．要使线段最长，则只须△的面积取大值时即可. ………………8分 设点坐标为（，则有: ‎ ‎　　　 ‎ ‎ 　 ＝‎ ‎　 ＝‎ ‎ ＝‎ ‎＝‎ ‎＝ ＝－‎ 即时，△的面积取大值，此时线段最长，则点坐标 为（－2，－3） ‎ ‎25．（长沙）已知：二次函数的图象经过点（1，0），一次函数图象经过原点和点（1，－b），其中且、为实数．‎ ‎（1）求一次函数的表达式（用含b的式子表示）；‎ ‎（2）试说明：这两个函数的图象交于不同的两点；‎ ‎（3）设（2）中的两个交点的横坐标分别为x1、x2，求| x1－x2 |的范围．‎ ‎25．解：（1）∵一次函数过原点∴设一次函数的解析式为y=kx ‎∵一次函数过（1，－b） ∴y=－bx ……………………………3分 ‎（2）∵y=ax2+bx－2过（1，0）即a+b=2 …………………………4分 由得 ……………………………………5分 ‎① ∵△＝‎ ‎∴方程①有两个不相等的实数根∴方程组有两组不同的解 ‎∴两函数有两个不同的交点． ………………………………………6分 ‎（3）∵两交点的横坐标x1、x2分别是方程①的解 ‎∴ ‎ ‎∴＝‎ 或由求根公式得出 ………………………………………………………8分 ‎∵a>b>0，a+b=2 ∴2>a>1‎ 令函数 ∵在1