中考数学二模试卷含解析2 14页

‎2016年内蒙古巴彦淖尔市磴口县诚仁中学中考数学二模试卷 一、选择题（本大题共10小题，每小题4分，共40分．）‎ ‎1．的相反数是（　　）‎ A．﹣ B． C．﹣ D．‎ ‎2．2014年我国国内生产总值约为636000亿元，数字636000用科学记数法表示为（　　）‎ A．63.6×104 B．0.636×106 C．6.36×105 D．6.36×106‎ ‎3．下列图形中既是轴对称图形又是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎4．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（　　）‎ A．30° B．25° C．20° D．15°‎ ‎5．下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2：‎ 甲 乙 丙 丁 平均数（cm）‎ ‎561‎ ‎560‎ ‎561‎ ‎560‎ 方差s2（cm2）‎ ‎3.5‎ ‎3.5‎ ‎15.5‎ ‎16.5‎ 根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（　　）‎ A．甲 B．乙 C．丙 D．丁 ‎6．下列四个几何体：‎ 其中左视图与俯视图相同的几何体共有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎7．下列运算，结果正确的是（　　）‎ A．m2+m2=m4 B．（m+）2=m2+‎ C．（3mn2）2=6m2n4 D．2m2n÷=2mn2‎ ‎8．半径为1的圆中有一条弦，如果它的长为，那么这条弦所对的圆周角为（　　）‎ A．60° B．120° C．45° D．60°或120°‎ ‎9．甲骑摩托车从A地去B地，乙开汽车从B地去A地，同时出发，匀速行驶，各自到达终点后停止，设甲、乙两人间距离为s（单位：千米），甲行驶的时间为t（单位：小时），s与t之间的函数关系如图所示，有下列结论：‎ ‎①出发1小时时，甲、乙在途中相遇；‎ ‎②出发1.5小时时，乙比甲多行驶了60千米；‎ ‎③出发3小时时，甲、乙同时到达终点；‎ ‎④甲的速度是乙速度的一半．‎ 其中，正确结论的个数是（　　）‎ A．4 B．3 C．2 D．1‎ ‎10．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列五个结论中：‎ ‎①2a﹣b＜0；②abc＜0；③a+b+c＜0；④b2﹣4ac＞0； ⑤（a+c）2＞b2，‎ 正确的有（　　）（填序号）‎ A．①②③ B．①③⑤ C．①③④ D．①②③⑤‎ ‎　‎ 二、填空题（每小题4分，满分24分.请把答案填在答题卡上对应的横线上.）‎ ‎11．要使式子有意义，则a的取值范围为　　　　　　．‎ ‎12．韩国发生中东呼吸综合症，一人感染，经过两轮传染后共有81人感染，这种传染病每轮传染中平均一个人传染了x个人？列方程为　　　　　　．‎ ‎13．一个圆锥的侧面积为8π，母线长为4，则这个圆锥的全面积为　　　　　　．‎ ‎14．已知关于x的一元二次方程m2x2+（2m﹣1）x+1=0有两个不相等的实数根，则m的取值范围是　　　　　　．‎ ‎15．不等式组：的解集是　　　　　　．‎ ‎16．若（x2+y2）2﹣5（x2+y2）﹣6=0，则x2+y2=　　　　　　．‎ ‎　‎ 三、解答题（共86分．解答应写出文字说明、证明过程或演算步骤）‎ ‎17．（1）计算：π﹣3.14）0‎ ‎（2）先化简÷（a﹣2+），然后从﹣2，﹣1，1，2四个数中选择一个合适的数作为a的值代入求值．‎ ‎（3）解分式方程： +=1．‎ ‎18．如图，四边形ABCD为菱形，M为BC上一点，连接AM交对角线BD于点G，并且∠ABM=2∠BAM．‎ ‎（1）求证：AG=BG；‎ ‎（2）若点M为BC的中点，同时S△BMG=1，求三角形ADG的面积．‎ ‎19．自实施新教育改革后，学生的自主学习、合作交流能力有很大提高，张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分同学进行了为期半个月的跟踪调查，并将调查结果分为四类：A．特别好；B．好；C．一般；D．较差，并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：‎ ‎（1）本次调查中，张老师一共调查了多少名同学？‎ ‎（2）求出调查中C类女生及D类男生的人数，将条形统计图补充完整；‎ ‎（3）为了共同进步，张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．‎ ‎20．如图，一次函数y=﹣x+4的图象与反比例函数y=（k为常数，且k≠0）的图象交于A（1，a），B两点．‎ ‎（1）求反比例函数的表达式及点B的坐标；‎ ‎（2）直接写出一次函数y=﹣x+4的值大于反比例函数y=的值自变量x的范围；‎ ‎（3）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标及△PAB的面积．‎ ‎21．如图，在测量塔高AB时，选择与塔底在同一水平面的同一直线上的C、D两点，用测角仪器测得塔顶A的仰角分别是30°和60°，已知测角仪器高CE=1.5米，CD=30米，求塔高AB．（保留根号）‎ ‎22．为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40元，超市规定每盒售价不得少于45元．根据以往销售经验发现：当售价定为每盒45元时，每天可卖出700盒，每盒售价每提高1元，每天要少卖出20盒．‎ ‎（1）试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；‎ ‎（2）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？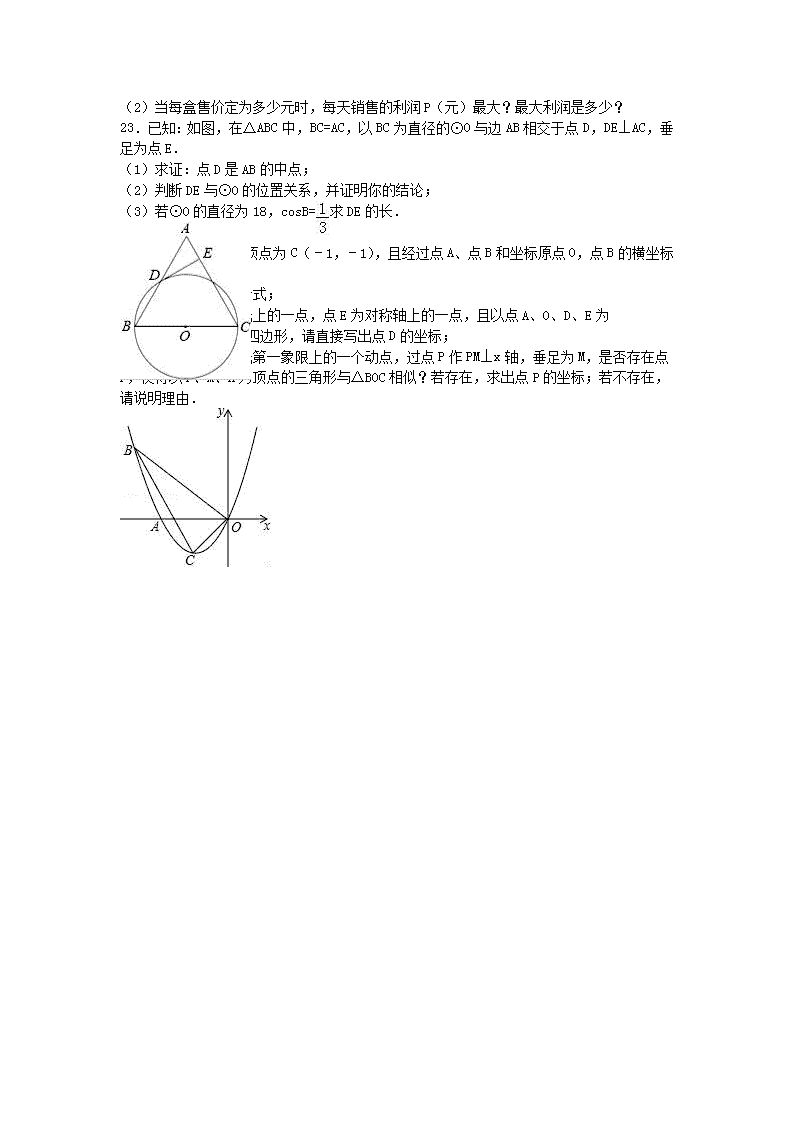‎ ‎23．已知：如图，在△ABC中，BC=AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．‎ ‎（1）求证：点D是AB的中点；‎ ‎（2）判断DE与⊙O的位置关系，并证明你的结论；‎ ‎（3）若⊙O的直径为18，cosB=，求DE的长．‎ ‎24．如图，抛物线的顶点为C（﹣1，﹣1），且经过点A、点B和坐标原点O，点B的横坐标为﹣3．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若点D为抛物线上的一点，点E为对称轴上的一点，且以点A、O、D、E为 顶点的四边形为平行四边形，请直接写出点D的坐标；‎ ‎（3）若点P是抛物线第一象限上的一个动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎　‎ ‎2016年内蒙古巴彦淖尔市磴口县诚仁中学中考数学二模试卷 参考答案与试题解析 ‎　‎ 一、选择题（本大题共10小题，每小题4分，共40分．）‎ ‎1．的相反数是（　　）‎ A．﹣ B． C．﹣ D．‎ ‎【考点】实数的性质．‎ ‎【分析】由于互为相反数的两个数和为0，由此即可求解．‎ ‎【解答】解：∵+（﹣）=0，‎ ‎∴的相反数是﹣．‎ 故选A．‎ ‎　‎ ‎2．2014年我国国内生产总值约为636000亿元，数字636000用科学记数法表示为（　　）‎ A．63.6×104 B．0.636×106 C．6.36×105 D．6.36×106‎ ‎【考点】科学记数法—表示较大的数．‎ ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．‎ ‎【解答】解：将636000亿用科学记数法表示为：6.36×105亿元．‎ 故选：C．‎ ‎　‎ ‎3．下列图形中既是轴对称图形又是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎【考点】中心对称图形；轴对称图形．‎ ‎【分析】根据轴对称图形与中心对称图形的概念求解．‎ ‎【解答】解：A、既是轴对称图形，又是中心对称图形，故A正确；‎ B、不是轴对称图形，是中心对称图形，故B错误；‎ C、是轴对称图形，不是中心对称图形，故C错误；‎ D、是轴对称图形，不是中心对称图形，故D错误．‎ 故选：A．‎ ‎　‎ ‎4．如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是（　　）‎ A．30° B．25° C．20° D．15°‎ ‎【考点】平行线的性质．‎ ‎【分析】本题主要利用两直线平行，内错角相等作答．‎ ‎【解答】解：根据题意可知，两直线平行，内错角相等，‎ ‎∴∠1=∠3，‎ ‎∵∠3+∠2=45°，‎ ‎∴∠1+∠2=45°‎ ‎∵∠1=20°，‎ ‎∴∠2=25°．‎ 故选：B．‎ ‎　‎ ‎5．下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差s2：‎ 甲 乙 丙 丁 平均数（cm）‎ ‎561‎ ‎560‎ ‎561‎ ‎560‎ 方差s2（cm2）‎ ‎3.5‎ ‎3.5‎ ‎15.5‎ ‎16.5‎ 根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择（　　）‎ A．甲 B．乙 C．丙 D．丁 ‎【考点】方差；算术平均数．‎ ‎【分析】根据方差和平均数的意义找出平均数大且方差小的运动员即可．‎ ‎【解答】解：∵甲的方差是3.5，乙的方差是3.5，丙的方差是15.5，丁的方差是16.5，‎ ‎∴S甲2=S乙2＜S丙2＜S丁2，‎ ‎∴发挥稳定的运动员应从甲和乙中选拔，‎ ‎∵甲的平均数是561，乙的平均数是560，‎ ‎∴成绩好的应是甲，‎ ‎∴从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择甲；‎ 故选A．‎ ‎　‎ ‎6．下列四个几何体：‎ 其中左视图与俯视图相同的几何体共有（　　）‎ A．1个 B．2个 C．3个 D．4个 ‎【考点】简单几何体的三视图．‎ ‎【分析】左视图、俯视图是分别从物体左面和上面看，所得到的图形．‎ ‎【解答】解：正方体左视图、俯视图都是正方形，左视图与俯视图相同；‎ 球左视图、俯视图都是圆，左视图与俯视图相同；‎ 圆锥左视图、俯视图分别是三角形、有圆心的圆，左视图与俯视图不相同；‎ 圆柱左视图、俯视图分别是长方形、圆，左视图与俯视图不相同；‎ 即同一个几何体的左视图与俯视图相同的几何体共有2个．‎ 故选B．‎ ‎　‎ ‎7．下列运算，结果正确的是（　　）‎ A．m2+m2=m4 B．（m+）2=m2+‎ C．（3mn2）2=6m2n4 D．2m2n÷=2mn2‎ ‎【考点】分式的混合运算；整式的混合运算．‎ ‎【分析】A：根据整式的混合运算方法计算即可．‎ B：根据完全平方公式的计算方法判断即可．‎ C：根据积的乘方的运算方法计算即可．‎ D：根据分式的混合运算方法计算即可．‎ ‎【解答】解：∵m2+m2=2m2，‎ ‎∴选项A错误；‎ ‎∵（m+）2=m2++2，‎ ‎∴选项B错误；‎ ‎∵（3mn2）2=9m2n4，‎ ‎∴选项C错误；‎ ‎∵2m2n÷=2mn2，‎ ‎∴选项D正确．‎ 故选：D．‎ ‎　‎ ‎8．半径为1的圆中有一条弦，如果它的长为，那么这条弦所对的圆周角为（　　）‎ A．60° B．120° C．45° D．60°或120°‎ ‎【考点】圆周角定理．‎ ‎【分析】根据垂径定理求得AD的长，再根据三角形函数可得到∠AOD的度数，再根据圆周角定理得到∠ACB的度数，根据圆内接四边形的对角互补即可求得∠AEB的度数．‎ ‎【解答】解：如图，过O作OD⊥AB于D，则AD=AB=×=．‎ ‎∵OA=1，‎ ‎∴sin∠AOD==，∠AOD=60°．‎ ‎∵∠AOD=∠AOB=60°，∠ACB=∠AOB，‎ ‎∴∠ACB=∠AOD=60°．‎ 又∵四边形AEBC是圆内接四边形，‎ ‎∴∠AEB=180°﹣∠ACB=180°﹣60°=120°．‎ 故选D．‎ ‎　‎ ‎9．甲骑摩托车从A地去B地，乙开汽车从B地去A地，同时出发，匀速行驶，各自到达终点后停止，设甲、乙两人间距离为s（单位：千米），甲行驶的时间为t（单位：小时），s与t之间的函数关系如图所示，有下列结论：‎ ‎①出发1小时时，甲、乙在途中相遇；‎ ‎②出发1.5小时时，乙比甲多行驶了60千米；‎ ‎③出发3小时时，甲、乙同时到达终点；‎ ‎④甲的速度是乙速度的一半．‎ 其中，正确结论的个数是（　　）‎ A．4 B．3 C．2 D．1‎ ‎【考点】一次函数的应用．‎ ‎【分析】根据题意结合横纵坐标的意义得出辆摩托车的速度进而分别分析得出答案．‎ ‎【解答】解：由图象可得：出发1小时，甲、乙在途中相遇，故①正确；‎ 甲骑摩托车的速度为：120÷3=40（千米/小时），设乙开汽车的速度为a千米/小时，‎ 则，‎ 解得：a=80，‎ ‎∴乙开汽车的速度为80千米/小时，‎ ‎∴甲的速度是乙速度的一半，故④正确；‎ ‎∴出发1.5小时，乙比甲多行驶了：1.5×（80﹣40）=60（千米），故②正确；‎ 乙到达终点所用的时间为1.5小时，甲得到终点所用的时间为3小时，故③错误；‎ ‎∴正确的有3个，‎ 故选：B．‎ ‎　‎ ‎10．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列五个结论中：‎ ‎①2a﹣b＜0；②abc＜0；③a+b+c＜0；④b2﹣4ac＞0； ⑤（a+c）2＞b2，‎ 正确的有（　　）（填序号）‎ A．①②③ B．①③⑤ C．①③④ D．①②③⑤‎ ‎【考点】二次函数图象与系数的关系．‎ ‎【分析】由抛物线的对称轴大于﹣1，得出2a﹣b的符号，再由开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，根据对称轴在y轴的左右两侧得出b的符号，利用图象将x=1，﹣1代入函数解析式判断y的值，进而对所得结论进行判断．‎ ‎【解答】解：∵开口向下，‎ ‎∴a＜0，‎ ‎∵﹣＞﹣1，‎ ‎∴2a﹣b＜0，故①正确；‎ ‎∵抛物线与y轴的负半轴相交，‎ ‎∴c＜0，‎ ‎∵对称轴在y轴的左侧，‎ ‎∴b＜0，‎ ‎∴abc＜0，②正确；‎ 当x=1，﹣1时，y的值分别为a+b+c＜0和a﹣b+c＜0，故③⑤正确；‎ ‎∵抛物线和x轴没有交点，‎ ‎∴b2﹣4ac＜0，故④不正确；‎ 故选D．‎ ‎　‎ 二、填空题（每小题4分，满分24分.请把答案填在答题卡上对应的横线上.）‎ ‎11．要使式子有意义，则a的取值范围为　a≥﹣2且a≠0　．‎ ‎【考点】二次根式有意义的条件．‎ ‎【分析】根据二次根式的性质和分式的意义，被开方数大于或等于0，分母不等于0，可以求出x的范围．‎ ‎【解答】解：根据题意得：a+2≥0且a≠0，‎ 解得：a≥﹣2且a≠0．‎ 故答案为：a≥﹣2且a≠0．‎ ‎　‎ ‎12．韩国发生中东呼吸综合症，一人感染，经过两轮传染后共有81人感染，这种传染病每轮传染中平均一个人传染了x个人？列方程为　1+x+（1+x）x=81　．‎ ‎【考点】由实际问题抽象出一元二次方程．‎ ‎【分析】根据题意可以列出相应的方程，本题得以解决．‎ ‎【解答】解：根据题意可得，‎ ‎1+x+（1+x）x=81，‎ 故答案为：1+x+（1+x）x=81．‎ ‎　‎ ‎13．一个圆锥的侧面积为8π，母线长为4，则这个圆锥的全面积为　12π　．‎ ‎【考点】圆锥的计算．‎ ‎【分析】据扇形的面积公式求出扇形的圆心角，再利用弧长公式求出弧长，再利用圆的面积公式求出底面半径，求得底面积后即可求得全面积．‎ ‎【解答】解：∵=8π，‎ ‎∴解得n=180‎ 则弧长==4π ‎2πr=4π 解得r=2，‎ ‎∴底面积为4π，‎ ‎∴全面积为12π．‎ 故答案是：12π．‎ ‎　‎ ‎14．已知关于x的一元二次方程m2x2+（2m﹣1）x+1=0有两个不相等的实数根，则m的取值范围是　m＜且m≠0　．‎ ‎【考点】根的判别式．‎ ‎【分析】根据一元二次方程的根的判别式，建立关于m的不等式，求出m的取值范围．‎ ‎【解答】解：∵a=m，b=2m﹣1，c=1，方程有两个不相等的实数根，‎ ‎∴△=b2﹣4ac=（2m﹣1）2﹣4m2=1﹣4m＞0，‎ ‎∴m＜．‎ 又∵二次项系数不为0，‎ ‎∴m≠0‎ 即m＜且m≠0．‎ ‎　‎ ‎15．不等式组：的解集是　﹣2＜x≤1　．‎ ‎【考点】解一元一次不等式组．‎ ‎【分析】先求出两个不等式的解集，再求其公共解．‎ ‎【解答】解：（1）去分母得，﹣3x﹣3﹣x+3＜8，‎ 移项合并同类项得，﹣4x＜8，‎ 两边同时除以﹣4得，x＞﹣2；‎ ‎（2）去分母得，2（2x+1）﹣3（1﹣x）≤6，‎ 去括号得，4x+2﹣3+3x≤6，‎ 移项合并同类项得，7x≤7，‎ 系数化为1得，x≤1‎ 故不等式组的解集是﹣2＜x≤1．‎ ‎　‎ ‎16．若（x2+y2）2﹣5（x2+y2）﹣6=0，则x2+y2=　6　．‎ ‎【考点】换元法解一元二次方程．‎ ‎【分析】设x2+y2=t．则原方程转化为关于t的一元二次方程t2﹣5t﹣6=0，即（t﹣6）（t+1）=0；然后解关于t的方程即可．‎ ‎【解答】解：设x2+y2=t（t≥0）．则 t2﹣5t﹣6=0，即（t﹣6）（t+1）=0，‎ 解得，t=6或t=﹣1（不合题意，舍去）；‎ 故x2+y2=6．‎ 故答案是：6．‎ ‎　‎ 三、解答题（共86分．解答应写出文字说明、证明过程或演算步骤）‎ ‎17．（1）计算：π﹣3.14）0‎ ‎（2）先化简÷（a﹣2+），然后从﹣2，﹣1，1，2四个数中选择一个合适的数作为a的值代入求值．‎ ‎（3）解分式方程： +=1．‎ ‎【考点】分式的化简求值；零指数幂；负整数指数幂；解分式方程；特殊角的三角函数值．‎ ‎【分析】（1）原式利用绝对值的代数意义，零指数幂、负整数指数幂法则，特殊角的三角函数值，以及立方根定义计算即可得到结果；‎ ‎（2）原式括号中两项通分并利用同分母分式的加法法则计算，同时利用除法法则变形，约分得到最简结果，把a的值代入计算即可求出值；‎ ‎（3）分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．‎ ‎【解答】解：（1）原式=﹣1+4﹣﹣2﹣1=0；‎ ‎（2）原式=÷=•=，‎ 当a=2时，原式=3；‎ ‎（3）去分母得：2+x2+2x=x2﹣4，‎ 解得：x=﹣3，‎ 经检验x=﹣3是分式方程的解．‎ ‎　‎ ‎18．如图，四边形ABCD为菱形，M为BC上一点，连接AM交对角线BD于点G，并且∠ABM=2∠BAM．‎ ‎（1）求证：AG=BG；‎ ‎（2）若点M为BC的中点，同时S△BMG=1，求三角形ADG的面积．‎ ‎【考点】菱形的性质．‎ ‎【分析】（1）根据菱形的对角线平分一组对角，得出∠ABD=∠CBD，再根据∠ABM=2∠BAM，得出∠ABD=∠BAM，然后根据等角对等边证明即可．‎ ‎（2）根据相似三角形面积的比等于相似比的平方即可求得．‎ ‎【解答】（1）证明：∵四边形ABCD是菱形，‎ ‎∴∠ABD=∠CBD，‎ ‎∵∠ABM=2∠BAM，‎ ‎∴∠ABD=∠BAM，‎ ‎∴AG=BG；‎ ‎（2）解：∵AD∥BC，‎ ‎∴△ADG∽△MBG，‎ ‎∴=，‎ ‎∵点M为BC的中点，‎ ‎∴=2，‎ ‎∴=（）2=4‎ ‎∵S△BMG=1，‎ ‎∴S△ADG=4．‎ ‎　‎ ‎19．自实施新教育改革后，学生的自主学习、合作交流能力有很大提高，张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分同学进行了为期半个月的跟踪调查，并将调查结果分为四类：A．特别好；B．好；C．一般；D．较差，并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：‎ ‎（1）本次调查中，张老师一共调查了多少名同学？‎ ‎（2）求出调查中C类女生及D类男生的人数，将条形统计图补充完整；‎ ‎（3）为了共同进步，张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．‎ ‎【考点】条形统计图；扇形统计图；列表法与树状图法．‎ ‎【分析】（1）根据A类的人数是3，所占的百分比是15%，据此即可求得总人数；‎ ‎（2）根据百分比的意义求得C、D两类的人数，进而求得C类女生及D类男生的人数；‎ ‎（3）利用列举法表示出所有可能的结果，然后利用概率公式即可求解．‎ ‎【解答】解：（1）调查的总人数是：（1+2）÷15%=20（人）；‎ ‎（2）C类学生的人数是：20×25%=5（人），则C类女生人数是：5﹣3=2（人）；‎ D类的人数是：20×（1﹣50%﹣25%﹣15%）=4（人），则D类男生的人数是：4﹣1=3（人）；‎ 如图所示：‎ ‎（3）如图所示：‎ 则恰好是一位男同学和一位女同学的概率是：．‎ ‎　‎ ‎20．如图，一次函数y=﹣x+4的图象与反比例函数y=（k为常数，且k≠0）的图象交于A（1，a），B两点．‎ ‎（1）求反比例函数的表达式及点B的坐标；‎ ‎（2）直接写出一次函数y=﹣x+4的值大于反比例函数y=的值自变量x的范围；‎ ‎（3）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标及△PAB的面积．‎ ‎【考点】反比例函数综合题．‎ ‎【分析】（1）由点A在一次函数图象上即可求出a值，从而得出点A的坐标，根据点A的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数的关系式，再联立直线AB与反比例函数关系式成方程组，解方程组即可求出点B的坐标；‎ ‎（2）观察函数图象，结合反比例函数的对称性，根据函数图象的上下位置关系即可找出不等式的解集；‎ ‎（3）作点B关于x轴的对称点B′，连接AB′交x轴于点P，此时PA+PB的值最小．根据点B的坐标即可得出点B′的坐标，由点A、B′的坐标利用待定系数法即可求出直线AB′的函数关系式，令其y=0求出x值即可得出点P的坐标，再利用分割图形求面积法即可求出S△PAB的值．‎ ‎【解答】解：（1）∵点A（1，a）在一次函数y=﹣x+4的图象上，‎ ‎∴a=﹣1+4=3，‎ ‎∴点A的坐标为（1，3）．‎ ‎∵点A（1，3）在反比例函数y=（k为常数，且k≠0）的图象上，‎ ‎∴3=k，‎ ‎∴反比例函数的表达式为y=．‎ 联立直线AB与反比例函数的表达式，得：，‎ 解得：或，‎ ‎∴点B的坐标为（3，1）．‎ ‎（2）观察函数图象可知：当x＜0或1＜x＜3时，一次函数y=﹣x+4的图象在反比例函数y=的图象的上方，‎ 故﹣x+4＞的解集为：x＜0或1＜x＜3．‎ ‎（3）作点B关于x轴的对称点B′，连接AB′交x轴于点P，此时PA+PB的值最小，如图所示．‎ ‎∵点B（3，1），点B、B′关于x轴对称，‎ ‎∴点B′（3，﹣1）．‎ 设直线AB′的表达式为y=mx+n（m≠0），‎ 则，解得：，‎ ‎∴直线AB′的表达式为y=﹣2x+5．‎ 令y=﹣2x+5中y=0，则x=，‎ ‎∴点P的坐标为（，0）．‎ S△PAB=S△ABB′﹣S△PBB′=BB′•（xB﹣xA）﹣BB′•（xB﹣xP）=．‎ ‎　‎ ‎21．如图，在测量塔高AB时，选择与塔底在同一水平面的同一直线上的C、D两点，用测角仪器测得塔顶A的仰角分别是30°和60°，已知测角仪器高CE=1.5米，CD=30米，求塔高AB．（保留根号）‎ ‎【考点】解直角三角形的应用-仰角俯角问题．‎ ‎【分析】首先设AF=x．分析图形：根据题意构造直角三角形，本题涉及到两个直角三角形△AGF、△AEF，应利用其公共边AF构造等量关系，借助GE=CD=EF﹣GF=30，构造方程关系式，进而可求出答案．‎ ‎【解答】解：设AF=x；‎ 在Rt△AGF中，有GF==x，‎ 同理在Rt△AEF中，有EF==x．‎ 结合图形可得：GE=CD=EF﹣GF=30‎ 即x﹣x=30，‎ 解可得：x=15；故AB=15+‎ 答：塔高AB为15+米．‎ ‎　‎ ‎22．为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40元，超市规定每盒售价不得少于45元．根据以往销售经验发现：当售价定为每盒45元时，每天可卖出700盒，每盒售价每提高1元，每天要少卖出20盒．‎ ‎（1）试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；‎ ‎（2）当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？‎ ‎【考点】二次函数的应用．‎ ‎【分析】（1）根据“当售价定为每盒45元时，每天可以卖出700盒，每盒售价每提高1元，每天要少卖出20盒”即可得出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；‎ ‎（2）根据利润=1盒粽子所获得的利润×销售量列式整理，再根据二次函数的最值问题解答．‎ ‎【解答】解：（1）由题意得，y=700﹣20（x﹣45）=﹣20x+1600；‎ ‎（2）P=（x﹣40）（﹣20x+1600）=﹣20x2+2400x﹣64000=﹣20（x﹣60）2+8000，‎ ‎∵x≥45，a=﹣20＜0，‎ ‎∴当x=60时，P最大值=8000元，‎ 即当每盒售价定为60元时，每天销售的利润P（元）最大，最大利润是8000元．‎ ‎　‎ ‎23．已知：如图，在△ABC中，BC=AC，以BC为直径的⊙O与边AB相交于点D，DE⊥AC，垂足为点E．‎ ‎（1）求证：点D是AB的中点；‎ ‎（2）判断DE与⊙O的位置关系，并证明你的结论；‎ ‎（3）若⊙O的直径为18，cosB=，求DE的长．‎ ‎【考点】切线的判定与性质；勾股定理；圆周角定理；解直角三角形．‎ ‎【分析】（1）连接CD，由BC为直径可知CD⊥AB，又BC=AC，由等腰三角形的底边“三线合一”证明结论；‎ ‎（2）连接OD，则OD为△ABC的中位线，OD∥AC，已知DE⊥AC，可证DE⊥OC，证明结论；‎ ‎（3）连接CD，在Rt△BCD中，已知BC=18，cosB=，求得BD=6，则AD=BD=6，在Rt△ADE中，已知AD=6，cosA=cosB=，可求AE，利用勾股定理求DE．‎ ‎【解答】（1）证明：连接CD，‎ ‎∵BC为⊙O的直径，∴CD⊥AB，‎ 又∵AC=BC，‎ ‎∴AD=BD，即点D是AB的中点．‎ ‎（2）解：DE是⊙O的切线．‎ 证明：连接OD，则DO是△ABC的中位线，‎ ‎∴DO∥AC，‎ 又∵DE⊥AC，‎ ‎∴DE⊥DO即DE是⊙O的切线；‎ ‎（3）解：∵AC=BC，∴∠B=∠A，‎ ‎∴cosB=cosA=，‎ ‎∵cosB=，BC=18，‎ ‎∴BD=6，‎ ‎∴AD=6，‎ ‎∵cosA=，‎ ‎∴AE=2，‎ 在Rt△AED中，DE=．‎ ‎　‎ ‎24．如图，抛物线的顶点为C（﹣1，﹣1），且经过点A、点B和坐标原点O，点B的横坐标为﹣3．‎ ‎（1）求抛物线的解析式；‎ ‎（2）若点D为抛物线上的一点，点E为对称轴上的一点，且以点A、O、D、E为 顶点的四边形为平行四边形，请直接写出点D的坐标；‎ ‎（3）若点P是抛物线第一象限上的一个动点，过点P作PM⊥x轴，垂足为M，是否存在点P，使得以P、M、A为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎【考点】二次函数综合题．‎ ‎【分析】（1）根据顶点坐标设出抛物线的顶点式解析式，将原点坐标代入求出a的值，即可确定出抛物线解析式；‎ ‎（2）分三种情况考虑，D在第一象限，第二象限以及第三象限，利用平行四边形的性质及坐标与图形性质求出D坐标即可；‎ ‎（3）根据题意画出图形，根据B横坐标为﹣3，代入抛物线解析式求出纵坐标，确定出B坐标，进而求出BC，BO，OC的长，利用勾股定理的逆定理得到三角形BOC为直角三角形，若P、M、A为顶点的三角形与△BOC相似，设P（m，n），由题意得m＞0，n＞0，且n=m2+2m，根据相似得比例，列出关于m的方程，求出方程的解得到m的值，进而求出n的值，即可确定出P的坐标．‎ ‎【解答】解：（1）∵抛物线的顶点为C（﹣1，﹣1），‎ ‎∴设抛物线的解析式为：y=a（x+1）2﹣1，‎ ‎∵抛物线经过（0，0），‎ ‎∴将x=0，y=0代入抛物线解析式得：0=a﹣1，‎ 解得：a=1，‎ ‎∴y=（x+1）2﹣1=x2+2x，‎ 令y=0时，x2+2x=0，‎ 解得x1=0，x2=﹣2，‎ ‎∴A（﹣2，0）；‎ ‎（2）如图所示，分三种情况考虑：‎ 当D1在第一象限时，若四边形AOD1E1为平行四边形，‎ ‎∴AO=E1D1=2，‎ ‎∵抛物线对称轴为直线x=﹣1，‎ ‎∴D1横坐标为1，‎ 将x=1代入抛物线y=x2+2x=1+2=3，即D1（1，3）；‎ 当D2在第二象限时，同理D2（﹣3，3）；‎ 当D3在第三象限时，若四边形AE2OD3为平行四边形，此时D3与C重合，即D3（﹣1，﹣1）；‎ ‎（3）存在，‎ ‎∵点B在抛物线上，‎ ‎∴当x=﹣3时，y=9﹣6=3，‎ ‎∴B（﹣3，3），‎ 根据勾股定理得：BO2=9+9=18；CO2=1+1=2；BC2=16+4=20，‎ ‎∴BO2+CO2=18+2=20，‎ ‎∴BO2+CO2=BC2，∴△BOC为直角三角形，‎ 假设存在点P，使得以P、M、A为顶点的三角形与△BOC相似，‎ 设P（m，n），由题意得m＞0，n＞0，且n=m2+2m，‎ ‎①若△AMP∽△BOC，则=，即=，‎ 整理得：m+2=3（m2+2m）=0，即3m2+5m﹣2=0，‎ 解得：m1=，m2=﹣2（舍去），‎ m1=时，n=+=，‎ ‎∴P（，）；‎ ‎②若△AMP∽△COB，则=，即=，‎ 整理得：m2﹣m﹣6=0，‎ 解得 m1=3，m2=﹣2（舍去），‎ 当m=3时，n=9+6=15，‎ ‎∴P（3，15），‎ 综上所述，符合条件的点P有两个，分别是P1（，），P2（3，15）．‎