中考数学必考重点题型 12页

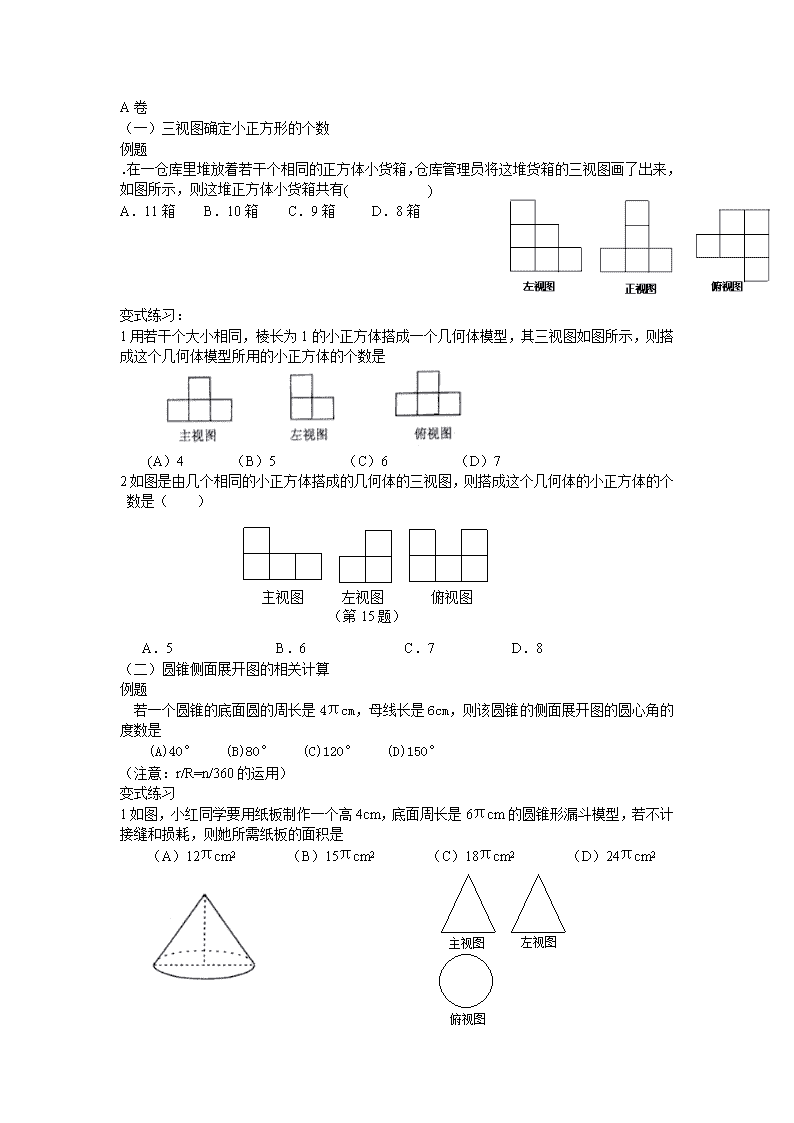
A卷 ‎（一）三视图确定小正方形的个数 例题 ‎ ‎．在一仓库里堆放着若干个相同的正方体小货箱，仓库管理员将这堆货箱的三视图画了出来，如图所示，则这堆正方体小货箱共有( ) ‎ A．11箱 B．10箱 C．9箱 D．8箱 变式练习：‎ ‎1用若干个大小相同，棱长为1的小正方体搭成一个几何体模型，其三视图如图所示，则搭成这个几何体模型所用的小正方体的个数是 ‎(A）4 （B）5 （C）6 （D）7‎ ‎2如图是由几个相同的小正方体搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是（ ）‎ 主视图 左视图 俯视图 俯视图 ‎（第15题）‎ ‎ A．5 B．‎6 C．7 D．8‎ ‎（二）圆锥侧面展开图的相关计算 例题 ‎ 若一个圆锥的底面圆的周长是4πcm，母线长是‎6cm，则该圆锥的侧面展开图的圆心角的度数是 ‎ (A)40° (B)80° (C)120° (D)150°‎ ‎（注意：r/R=n/360的运用）‎ 变式练习 ‎1如图，小红同学要用纸板制作一个高‎4cm，底面周长是6πcm的圆锥形漏斗模型，若不计接缝和损耗，则她所需纸板的面积是 ‎（A）12πcm2 （B）15πcm2 （C）18πcm2 （D）24πcm2‎ ‎ ‎ ‎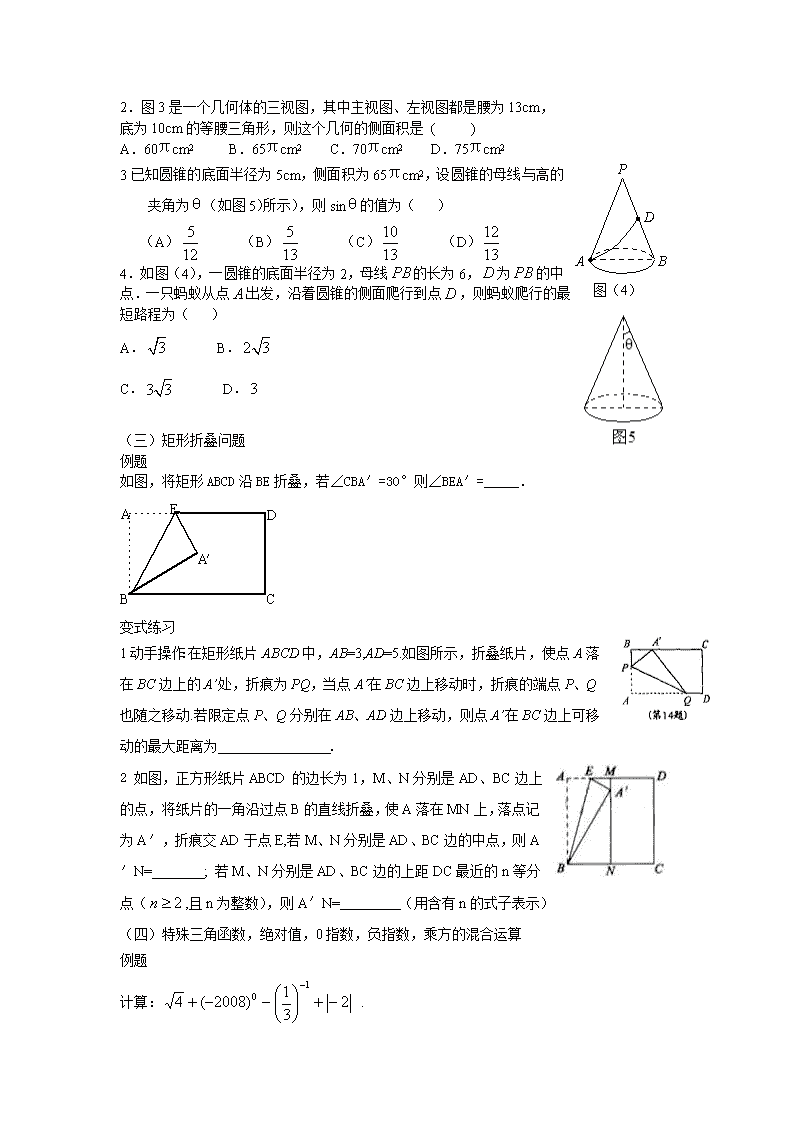2．图3是一个几何体的三视图，其中主视图、左视图都是腰为‎13cm，‎ 底为‎10cm的等腰三角形，则这个几何的侧面积是 ( )‎ A．60πcm2 B．65πcm‎2 C．70πcm2 D．75πcm2‎ P B A D 图（4）‎ ‎3已知圆锥的底面半径为‎5cm，侧面积为65πcm2，设圆锥的母线与高的夹角为θ（如图5）所示），则sinθ的值为（ ）‎ ‎（A） （B） （C） （D）‎ ‎4．如图（4），一圆锥的底面半径为2，母线的长为6，为的中点．一只蚂蚁从点出发，沿着圆锥的侧面爬行到点，则蚂蚁爬行的最短路程为（ ）‎ A．　 B． ‎ C．　 D．‎ ‎（三）矩形折叠问题 例题 如图，将矩形ABCD沿BE折叠，若∠CBA′=30°则∠BEA′=_____．‎ 变式练习 ‎1动手操作：在矩形纸片ABCD中，AB=3,AD=5.如图所示，折叠纸片，使点A落在BC边上的A’处，折痕为PQ，当点A’在BC边上移动时，折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动，则点A’在BC边上可移动的最大距离为 .‎ ‎2 如图，正方形纸片ABCD的边长为1，M、N分别是AD、BC边上的点，将纸片的一角沿过点B的直线折叠，使A落在MN上，落点记为A′，折痕交AD于点E,若M、N分别是AD、BC边的中点，则A′N= ; 若M、N分别是AD、BC边的上距DC最近的n等分点（,且n为整数），则A′N= （用含有n的式子表示）‎ ‎（四）特殊三角函数，绝对值，0指数，负指数，乘方的混合运算 例题 计算： .‎ 变式练习 ‎1计算：‎ ‎2计算：（－1）2009 + 3（tan 60°）－1－︱1－︱+（3.14－p）0．‎ ‎（五）化简求值，分式方程 例题 先化简，再选择一个合适的x值代入求值：．‎ 变式练习 ‎1解方程：=3．‎ ‎2 化简求值，其中。‎ ‎（六）解不等式组及在数轴上表示 例题 解不等式组并写出该不等式组的最大整式解.‎ 变式练习 ‎1.解不等式组并在所给的数轴上表示出其解集。‎ ‎2解不等式组并把解集在数轴上表示出来 ‎（七）一次函数与反比例函数过公共点，求解析式，点的坐标，面积等 例题 已知一次函数与反比例函数，其中一次函数的图象经过点P(，5)．‎ ‎ (1)试确定反比例函数的表达式；‎ ‎ (2)若点Q是上述一次函数与反比例函数图象在第三象限的交点，求点Q的坐标．‎ 变式练习 ‎1如图（12），一次函数的图象分别交轴、轴于两点，为的 中点，轴于点，延长交反比例函数的图象于点，且 yc Qc Ac Cc Pc Bc Oc xc 图（12）‎ ‎（1）求的值；‎ ‎（2）连结求证：四边形是菱形．‎ ‎2．（本小题9分）‎ 如图，反比例函数图象在第一象限的分支上有一点C（1，3），过点C的直线y = kx + b〔k < 0〕与x轴交于点A.‎ ‎（1）求反比例函数的解析式；‎ ‎（2）当直线与反比例函数的图象在第一象限内的另一交点 的横坐标为3时，求△COD的面积.‎ ‎ ‎ ‎3已知：如图，在平面直角坐标系中，直线AB分别与轴交于点B、A，与反比例函数的图象分别交于点C、D，轴于点E，．‎ ‎（1）求该反比例函数的解析式；‎ ‎（2）求直线AB的解析式．‎ O x y A C B E ‎19题图 D ‎（八）仰角，俯角与解直角三角形的结合的相关应用计算 例题 某中学九年级学生在学习“直角三角形的边角关系”一章时，开展测量物体高度的实践活动，他们要测量学校一幢教学楼的高度．如图，他们先在点C测得教学楼AB的顶点A的仰角为30°，然后向教学楼前进‎60米到达点D，又测得点A的仰角为45°。请你根据这些数据，求出这幢教学楼的高度．(计算过程和结果均不取近似值)‎ 变式练习 ‎1热气球的探测器显示，从热气球看一栋高楼顶部的仰角为，看这栋高楼底部的俯角为，热气球与高楼的水平距离为‎66 m，这栋高楼有多高？（结果精确到‎0.1 ‎m，参考数据：）‎ C A B C A B ‎60°‎ ‎45°‎ 北 北 ‎18题图 ‎2为打击索马里海盗，保护各国商船的顺利通行，我海军某部奉命前往该海域执行护航任务．某天我护航舰正在某小岛北偏西并距该岛海里的处待命．位于该岛正西方向处的某外国商船遭到海盗袭击，船长发现在其北偏东的方向有我军护航舰（如图9所示），便发出紧急求救信号．我护航舰接警后，立即沿航线以每小时60海里的速度前去救援．问我护航舰需多少分钟可以到达该商船所在的位置处？‎ ‎3如图，某中学九年级一班数学课外活动小组利用周末开展课外实践活动，他们要在某公园人工湖旁的小山AB上，测量湖中两个小岛C、D间的距离.从山顶A处测得湖中小岛C 的俯角为60°，测得湖中小岛D的俯角为45°.已知小山AB的高为‎180米，求小岛C、D间的距离.（计算过程和结果均不取近似值）‎ ‎（九）概率的应用，树形图求概率及游戏规则的修改 例题 有一枚均匀的正四面体，四个面上分别标有数字l，2，3，4，小红随机地抛掷一次，把着地一面的数字记为x；另有三张背面完全相同，正面上分别写有数字一2，一l，1的卡片，小亮将其混合后，正面朝下放置在桌面上，并从中随机地抽取一张，把卡片正面上的数字记为y；然后他们计算出S=x+y的值．‎ ‎ (1)用树状图或列表法表示出S的所有可能情况；‎ ‎ (2)分别求出当S=0和S<2时的概率．‎ 变式练习 ‎1一不透明纸箱中装有形状、大小、质地等完全相同的4个小球，分别标有数字1，2，3，4.‎ ‎（1）从纸箱中随机地一次取出两个小球，求这两个小球上所标的数字一个是奇数另一个是偶数的概率；‎ ‎（2）先从纸箱中随机地取出一个小球，用小球上所标的数字作为十位上的数字；将取出的小球放回后，再随机地取出一个小球，用小球上所标的数字作为个位上的数字，则组成的两位数恰好能被3整除的概率是多少？试用树状图或列表法加以说明.‎ ‎2有两个可以自由转动的均匀转盘A、B，均被分成4等份，并在每份内都标有数字（如图所示）．李明和王亮同学用这两个转盘做游戏．阅读下面的游戏规则，并回答下列问题：‎ ‎（1）用树状图或列表法，求两数相加和为零的概率；‎ ‎（2）你认为这个游戏规则对双方公平吗？若公平，请说明理由；若不公平，请修改游戏规则中的赋分标准，使游戏变得公平．‎ ‎3‎ ‎2‎ ‎0‎ ‎1‎ ‎0‎ ‎（第26题图）‎ Ａ Ｂ ‎(十) ‎ 三角形，四边形，圆有关的计算证明及探究 例题 ‎．已知A、D是一段圆弧上的两点，且在直线的同侧，分别过这两点作的垂线，垂足为B、C，E是BC上一动点，连结AD、AE、DE，且∠AED=90°。‎ ‎（1）如图①，如果AB=6,BC=16,且BE:CE=1:3，求AD的长。‎ ‎（2）如图②，若点E恰为这段圆弧的圆心，则线段AB、BC、CD之间有怎样的等量关系？请写出你的结论并予以证明。再探究：当A、D分别在直线两侧且AB≠CD，而其余条件不变时，线段AB、BC、CD之间又有怎样的等量关系？请直接写出结论，不必证明。‎ 变式练习 ‎1已知：在梯形ABCD中，AD∥BC，AB = DC，E、F分别是AB和BC边上的点.‎ ‎（1）如图①，以EF为对称轴翻折梯形ABCD，使点B与点D重合，且DF⊥BC.若AD =4，BC=8，求梯形ABCD的面积的值；‎ ‎（2）如图②，连接EF并延长与DC的延长线交于点G，如果FG=k·EF（k为正数），试猜想BE与CG有何数量关系？写出你的结论并证明之.‎ ‎2图8-2‎ 图8-1‎ 如图8-1，已知O是锐角∠XAY的边AX上的动点，以点O为圆心、R为半径的圆与射线AY切于点B，交射线OX于点C．连结BC，作CD⊥BC，交AY于点D．‎ ‎(1) (3分) 求证：△ABC∽△ACD；‎ ‎(2) (6分) 若P是AY上一点，AP=4，且sinA=，‎ ‎① 如图8-2，当点D与点P重合时，求R的值；‎ ‎② 当点D与点P不重合时，试求PD的长(用R表示)．‎ B卷 ‎（一）迭代法求值，整体代入求值 例题 已知y = x – 1,那么x2 – 2xy + 3y2 – 2的值是 .‎ 变式练习 ‎1.若，则 ．‎ ‎2： 则代数式的值为。‎ ‎（二）根与系数的关系 例题 已知实数 且求的值 变式练习 ‎1已知关于的方程 ‎ ‎ ① 当m取去什么值时，原方程没有实数根? ‎ ‎②取一个非零整数m，使原方程有两个实数根，并求这两个实数根的平方和。‎ ‎2若m、n是方程的两个根，则 ‎ ‎3若、 是方程的两个实数根，则的值是 ‎ ‎（三）规律问题 例题 已知，记，，…，，则通过计算推测出的表达式＝_______．‎ 变式练习 ‎1若n为整数，且n≤x1的常数），设过Q、R两点，且以QR的垂直平分线为对称轴的抛物线与y轴的交点为N，其顶点为M，记△QNM的面积为，△QNR的面积，求∶的值.‎ ‎ ‎