中考复习 三角形全等相似练习题 10页

中考复习 三角形全等、相似练习题 一、选择题：（本大题共6题，每题4分，满分24分）‎ ‎1.下列命题中是真命题的是………………………………………（ ）‎ ‎（A）直角三角形都相似； （B）等腰三角形都相似；‎ ‎（C）锐角三角形都相似； （D）等腰直角三角形都相似.‎ ‎2．如果∽，，那么的周长和的周长之比是……………………………………（ ）‎ ‎（A） ； （B） ； （C）； （D）．‎ ‎3．如图，在△中，∥，分别与、相交于点、，若则︰的值为（ ）.‎ ‎（A） ； （B） ； （C）； （D）．‎ ‎ 4. 已知≌，若的各边长分别3、4、5， 的最大角的度数是…………………………………… ( ).‎ ‎(A) 30°； (B) 60 ° ； (C) 90° ； (D) 120°.‎ ‎5．在△ABC中，D、E分别是AB、AC上的点，下列命题中不正确的是（ ）．‎ ‎（A）若DE//BC，则 ； （B）若，则 DE//BC；‎ ‎（C）若DE//BC，则 ； （D）若，则DE//BC . ‎ ‎6．在△ABC中，D、E分别是AB、AC上的点，DE∥BC，且DE平分△ABC的面积，则DE∶BC等于 ……………………………………………………………( )‎ ‎ （A）； （B）； （C）； （D）． ‎ 二、填空题：（本大题共12题，每4分，满分48分）‎ ‎7. 在中,点D、E分别在AB、AC边上,DE//BC，且DE=2，BC=5，CE=2，则AC = ．‎ ‎8.若△ABC∽△DEF，∠A=64°、∠B=36°则△DEF别中最小角的度数是___________．‎ ‎9. 如果线段AB=‎4cm，点P是线段AB的黄金分割点，那么较短线段BP= cm ‎10. 若两个相似三角形的周长比是4：9，则对应中线的比是 . ‎ ‎11.如图，在等边△ABC中，，点O在AC上，且，点P是AB上一动点，联接OP，以O为圆心，OP长为半径画弧交BC于点D, 联接PD，如果，那么AP的长是 .‎ 第12题图 ‎12. 如图，将沿直线平移到，使点和重合，连结交于点，若的面积是36，则的面积Ａ Ｐ Ｃ Ｂ 是 .‎ ‎13．如图，在中，是上一点，联结，‎ 要使，还需要补充一个条件.‎ 第13题图 这个条件可以是 ．‎ ‎14. 在平面直角坐标系内，将绕点逆时针旋转，得到．若点的坐标为(2，1)点B的坐标为（2，0），则点的坐标为 ．‎ A E F D B C ‎15．如果两个相似三角形的对应角平分线的比是2︰3，其中较大的一个三角形的面积是‎36cm2，那么另一个三角形的面积是_____________cm2‎ 第16题图 ‎16．如图,点D是Rt的斜边AB上的点,, 垂足为点E,, 垂足为点F,若AF=15,BE=10, 则四边形DECF的面积是 ．‎ Ａ D C F B ‎17.在△ABC中，D、E分别在AB、AC上，AD=3，BD=2 ，AC=10，EC=4，则 .‎ 第18题图 ‎18． 如图，梯形中，∥，，点在边上，，若△ABF与△FCD相似，则的长为 ．‎ 三、简答题（本大题共4题，每小题10分，满分40分）‎ A E C B F D G ‎19． 如图，在中，是的中点，是线段延长线上一点，过点作∥交的延长线于点，联结．‎ 求证：（1）四边形是平行四边形；‎ ‎（2）． ‎ ‎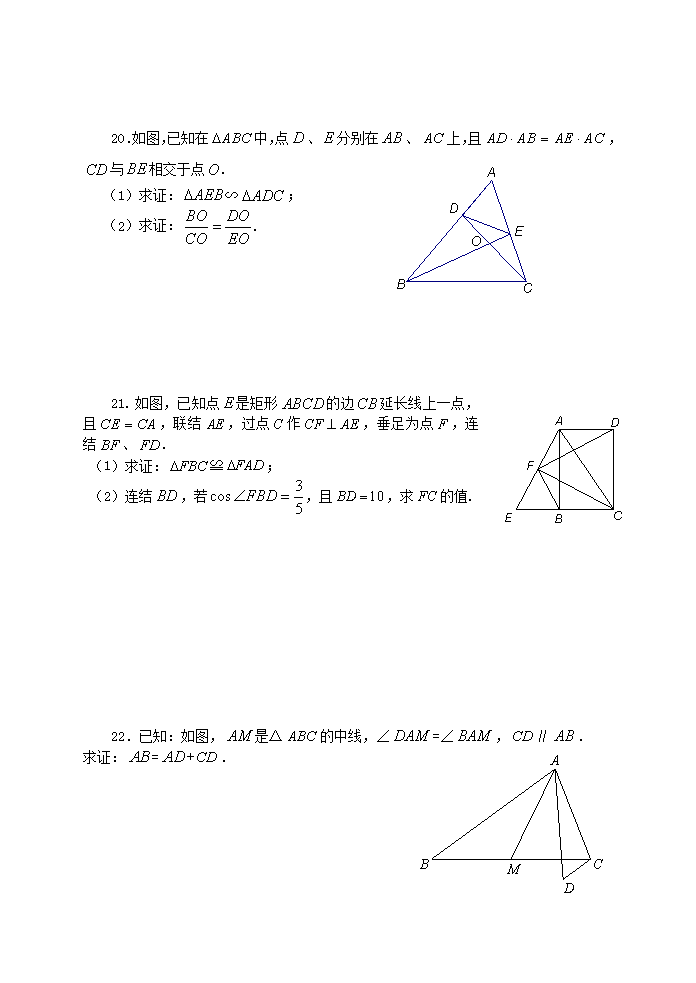20．如图，已知在中，点、分别在、上，且，与相交于点.‎ ‎（1）求证：∽；‎ ‎（2）求证：.‎ ‎21.如图，已知点是矩形的边延长线上一点，且，联结，过点作，垂足为点，连结、.‎ ‎（1）求证：≌；‎ ‎（2）连结，若，且，求的值. ‎ ‎22．已知：如图，是△的中线，∠=∠，∥．‎ A B C M D 求证：=+．‎ 四、解答题（本大题共3题，23-24每题12分，25题14分，满分38分）‎ ‎23. 如图，在中，，，垂足为点，、分别是、边上的点，且，. ‎ ‎（1）求证：；（2）求的度数. ‎ A B C D F E ‎24.如图，直线(＞)与分别交于点,，抛物线经过点，顶点在直线上．‎ ‎（1）求的值； ‎ ‎（2）求抛物线的解析式； ‎ ‎（3）如果抛物线的对称轴与轴交于点，那么在对称轴上找一点，使得 和相似，求点的坐标． ‎ A B O ‎25. 已知在等腰三角形中，，是的中点， 是上的动点（不与、重合），联结，过点作射线，使，射线交射线于点，交射线于点.‎ ‎（1）求证：∽；‎ ‎（2）设.‎ ‎①用含的代数式表示；‎ ‎②求关于的函数解析式，并写出的定义域.‎ 参考答案 一、1．D， 2．B， 3．A，4． C， 5. D， 6. C， ‎ 二、7. ；8．36°；9．； 10. 4∶9； 11. 6； 12． 18；‎ ‎ 13．答案不惟一，（或或或）； 14．(-1,2)； 15．16； 16. 150； 17． 9∶25； 18．2或8； ‎ 三、19．证明:(1) ∵∥, ∴ …………………1分 ‎ ∵ ‎ ‎ ∴ ≌ ……………………2分 ‎ ∴ ……………………1分 ‎ ∴ 四边形是平行四边形 ……………………1分 ‎ (2) ∵ 四边形是平行四边形 ‎ ∴ ……………………1分 ‎ ∵∥, ∴ ……………………1分 ‎ ∴ ∽ ……………………1分 ‎ ∴ ……………………1分 ‎∴ 即 …………1分 ‎20． 证明：（1）∵,∴ ………………1分 ‎ 又……………………………………………………1分 ‎ ∴∽……………………………………………1分 ‎（2） ∵∽‎ ‎ ∴……………………………………………2分 ‎ ∵……………………………………………2分 ‎ ∴∽……………………………………………1分 ‎ ∴ ………………………………………………2分 ‎21.（1）证明：,∴ …………………1分 ‎∵四边形是矩形，‎ ‎∴………………………………………1分 ‎∴在中，…………………………………………… 1分 ‎∴ ……………………………………………………… 1分 ‎∴……………………………………………………… 1分 ‎∴≌……………………………………………………… 1分 ‎（2）∵≌,………………… 1分 ‎∴…………………… 1分 ‎…………………………………………………………………… 1分 ‎…………………………………………………………………… 1分 ‎22．证明：分别延长、相交于点．‎ ‎∵∥，∴∠＝∠．……………………………2分 又∵∠＝∠，=，∴△≌△…………2分 ‎∴=． ………………………………………………………………1分 ‎∵∠＝∠，∠＝∠，∴∠＝∠．…2分 ‎∴=．…………………………………………………………2分 ‎∴==＋．………………………………………………1分 四、‎ ‎23. 证明：（1）∵，,‎ ‎∴，………………………………………………1分 又…………………………………………………………………1分 ‎∴∽…………………………………………………………1分 ‎∴ ………………………………………………………………1分 ‎∴………………………………………………………………1分 ‎（2）∵，‎ ‎∴…………………………………………………1分 ‎∴………………………………………………………2分 ‎∵，‎ ‎∴……………………………………………………………1分 ‎∴∽ ………………………………………………………1分 ‎∴…………………………………………………………1分 ‎∵,‎ ‎∴………………………………………1分 ‎24. （本题满分12）‎ 解:(1) ∵ 直线与分别交于点,‎ ‎ ∴ , ……………………………1分 ‎ ∵ ＞，∴ ‎ ‎ ∴ ……………………………1分 ‎ 解得，（舍去）‎ ‎ ∴ ……………………………1分 ‎ （2）方法一：由（1）得，，∴ ……………………………1分 ‎ ∵ 抛物线的顶点 ‎ ‎∵ 抛物线的顶点在直线上 ‎ 又 抛物线经过点 ‎∴ 解得， ………………………2分 ‎∴ 抛物线的解析式为： ……………………………1分 方法二： 由（1）得，，∴ ……………………………1分 ‎ 当时，‎ ‎ ∴ 抛物线经过原点 ‎ ∴ 抛物线的对称轴是直线 ‎ ‎ 设抛物线的顶点 ∵ 顶点在直线上 ‎ ∴ ， ∴ …………………………1分 ‎ 设抛物线 ‎ ∵ 抛物线过原点 ∴ 解得，……1分 ‎ ∴ 抛物线的解析式为：（或） ……1分 ‎ （3）由（2）可得，抛物线的对称轴是直线 得 ‎ ‎∵、、‎ 在，且 在，且 ‎∴ 当或时，∽ …1分 ‎∴ 这样的点有四个，即．……4分 ‎25.解：∵,∴…………………………………………1分 ‎∵…………………………………………1分 又,∴………………………………………1分 ‎∽ ………………………………………………………1分 ‎（2）①∵∽，∴…………………………2分 ‎∵是的中点，，∴，又 ∵‎ ‎∴当点在线段的延长线上时，‎ ‎，∴…………………………………………1分 当点在线段上时，‎ ‎，∴…………………………………………1分 ‎②过点作DG∥AB,交于点…………………………………1分 ‎∴，∴………………………1分 ‎∴当点在线段的延长线上时，‎ ‎∴，∴…………………………………………1分 ‎∴………………………………………………1分 当点在线段上时，‎ ‎∴，∴………………………………………1分 ‎∴………………………………………………1分