20132014西城中考一模数学试题 10页

北京市西城区2014年初三一模试题 ‎ 数 学 2014.4‎ 考生须知 ‎1．本试卷共6页，共五道大题，25道小题，满分120分，考试时间120分钟。‎ ‎2．在试卷和答题纸上认真填写学校名称、姓名和准考证号。‎ ‎3．试题答案一律填涂或书写在答题纸上，在试卷上作答无效。‎ ‎4. 在答题纸上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答。‎ ‎5．考试结束，请将本试卷、答题纸和草稿纸一并交回。‎ 一、选择题（本小题共32分，每小题4分）‎ ‎ 下面各题均有四个选项，其中只有一个是符合题意的。‎ ‎1. 的绝对值是（ ）‎ ‎ A. B. C. D. ‎ ‎2. ‎2014年3月5日，李克强总理在政府工作报告中指出：2013年全国城镇新增就业人数约13 100 000人，创历史新高，将数字13 100 000用科学计数法表示为（ ）‎ 主视方向 ‎ A. B. C. D. ‎ ‎3. 由5个相同的正方体组成的几何体如图所示，则它的主视图是（ ）‎ D.‎ C.‎ B.‎ A.‎ O B A C D 第5题图 ‎4. 从1到9这九个自然数中任取一个，是奇数的概率是（ ）‎ ‎ A. B. C. D. ‎ ‎5. 右图表示一圆柱形输水管的横截面，阴影部分为有水部分，如果输水管的半径为，‎ 水面宽为，则水的最大深度为（ ）‎ ‎ A. B. C. D. ‎ ‎6. 为了解某小区家庭使用垃圾袋的情况，小亮随机调查了该小区10户家庭一周垃圾袋的使用量，结果如 下：7，9，11，8，7，14，10，8，9，7（单位：个），关于这组数据下列结论正确的是（ ）‎ ‎ A.极差是6 B.众数是‎7 C.中位数是8 D.平均数是10‎ ‎7. 已知关于的一元二次方程有两个不相等的实数根，则的取值范围是（ ）‎ ‎ A. B. C. 且 D. 且 ‎8. 如图，在平面直角坐标系中，以点为顶点任作一直角，使其两边分别与轴、轴 的正半轴交于点、，连接，过点作于点，设点的横坐标为，的长为，‎ 则下列图象中，能表示与的函数关系的图象大致是（ ）‎ 第8题图 P H ‎1‎ ‎2‎ ‎3‎ y x O A Q ‎1‎ ‎2‎ A.‎ O x y ‎2‎ ‎3‎ ‎6.5‎ B.‎ O x y ‎2‎ ‎3‎ ‎6.5‎ C.‎ O x y ‎2‎ ‎3‎ ‎6.5‎ D.‎ O x y ‎2‎ ‎3‎ ‎6.5‎ 二、填空题（本题共16分，每小题4分）‎ ‎9. 分解因式： 。‎ ‎10. 写出一个只含字母的分式，满足的取值范围是，所写的分式是： 。‎ A B C D E O F 第11题图 ‎11. 如图，菱形中，，于点，且，连接，则的度 数为 度。‎ ‎12. 如图，在平面直角坐标系中，点，，‎ 正六边形沿轴正方向无滑动滚动，当点第一次落 在轴上时，点的坐标为： ；在运动过程中，点 的纵坐标的最大值是 ；保持上述运动过程，经过 的正六边形的顶点是 。‎ ‎1‎ ‎2‎ ‎3‎ y x O ‎1‎ ‎2‎ ‎3‎ ‎4‎ A B C D E F ‎1‎ ‎2‎ ‎3‎ y x O ‎1‎ ‎2‎ ‎3‎ ‎4‎ A B C D E F 三、解答题（本题共30分，每小题5分）‎ ‎13. 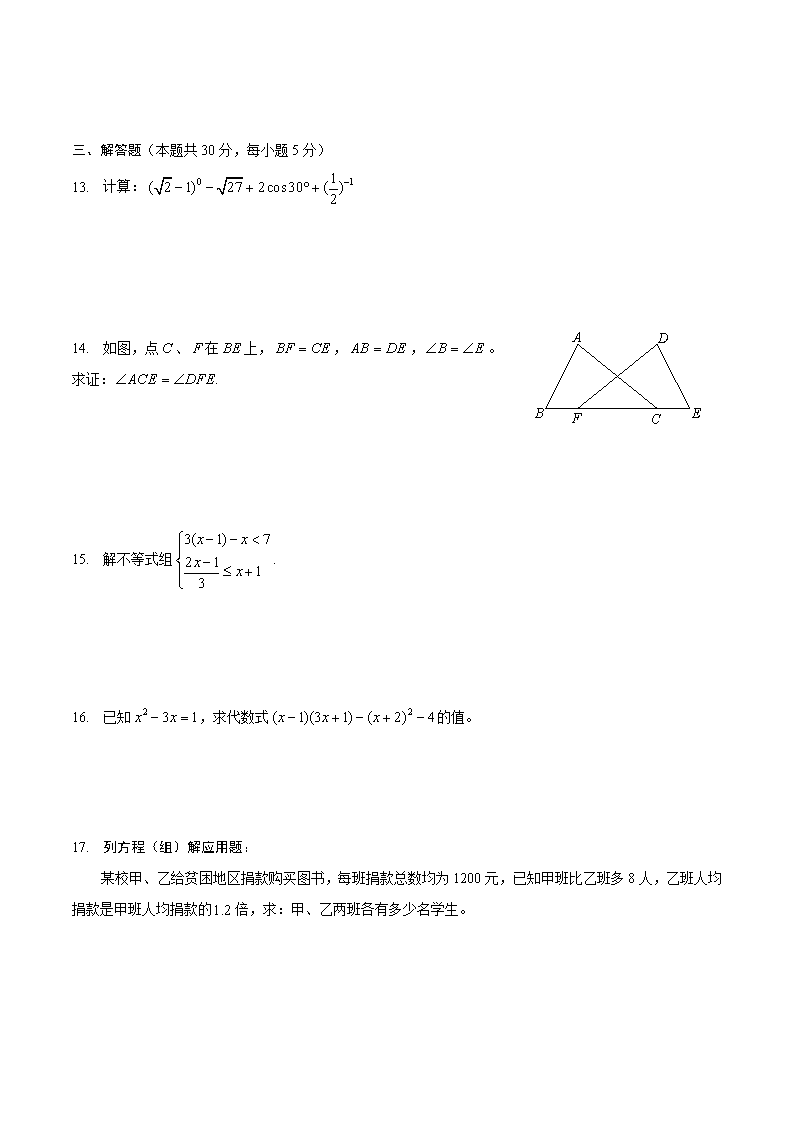计算：‎ A B C D E F ‎14. 如图，点、在上，，，。‎ 求证：‎ ‎15. 解不等式组.‎ ‎16. 已知，求代数式的值。‎ ‎17. 列方程（组）解应用题：‎ 某校甲、乙给贫困地区捐款购买图书，每班捐款总数均为1200元，已知甲班比乙班多8人，乙班人均 捐款是甲班人均捐款的倍，求：甲、乙两班各有多少名学生。‎ ‎18. 平面直角坐标系中，一次函数和反比例函数的图象都经过点。‎ ‎（1）求的值和一次函数的表达式；‎ ‎（2）点在双曲线上，且位于直线的下方，若点的横、纵坐标都是整数，直接写出点 O x y ‎－1‎ ‎－2‎ ‎1‎ ‎2‎ ‎1‎ ‎2‎ 的坐标。‎ 四、解答题（本题共20分，每小题5分）‎ ‎19. 如图，在中，，平分，且.‎ ‎（1）求证：四边形是矩形；‎ ‎（2）若是边长为的等边三角形，，相交于点，在上截取，连接，求 A B C D E F O 线段的长及四边形的面积。‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 收入∕万元 年份 ‎1.3‎ ‎2.9‎ ‎2010‎ ‎1.5‎ ‎3.3‎ ‎2011‎ ‎2012‎ ‎2013‎ ‎4‎ ‎1.8‎ 农民 城镇居民 北京市2010—2013年城镇居民人均可支配收入和农民人均现金收入统计图 ‎20. 以下是根据北京市统计局公布的2010—2013年北京市城镇居民人均可支配收入和农民人均现金收入的数据绘制的统计图的一部分：‎ ‎0‎ ‎5‎ ‎10‎ ‎15‎ ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ 年份 增长率（％）‎ ‎8.7‎ ‎13.8‎ ‎9.1‎ ‎11.1‎ 北京市2010—2013年城镇居民人均可支配收入的年增长率统计图 根据以上信息，解答下列问题：‎ ‎（1）2012年农民人均现金收入比2011年城镇居民人均可支配收入的一半少0.05万元，则2012年农民人 均现金收入是 万元，请根据以上信息补全条形统计图，并标明相应的数据（结果精确到0.1）；‎ ‎（2）在2010—2013年这四年中，北京市城镇居民人均可支配收入和农民人均现金收入相差数额最大的年 份是 年；‎ ‎（3）①2011—2013年城镇居民人均可支配收入的年平均增长率最接近 ；‎ ‎ A.14％ B.11％ C.10％ D.9％‎ ‎ ②若2014年城镇居民人均可支配收入按①中的年平均增长率增长，请预测2014年的城镇居民人均可 支配收入为 万元（结果精确到0.1）。‎ ‎21. 如图，在中，，以为直径作⊙，交于点，连接，过点作⊙的 O A B C D E F 切线，交延长线于点，交于点。‎ ‎（1）求证：；‎ ‎（2）当，时，求及的长。‎ ‎22. 阅读下列材料：‎ 问题：在平面直角坐标系中，一张矩形纸片按图1所示放置。已知，，‎ 将这张纸片折叠，使点落在边上，记作点，折痕与边（含端点）交于点，与边（含端 点）或其延长线交于点，求点的坐标。‎ 小明在解决这个问题时发现：要求点的坐标，只要求出线段的长即可，连接，设折痕所 在直线对应的函数表达式为：，于是有，，所以在 x y O B C D A E F 图22-1‎ 中，得到，在中，利用等角的三角函数值相等，就可以求出线段的长（如图 y 图22-2‎ x O C D B y 图22-2‎ x O C D B A ‎1）‎ 请回答：‎ ‎（1）如图1，若点的坐标为，直接写出点的坐标；‎ ‎（2）在图2中，已知点落在边上的点处，请画出折痕所在的直线（要求：尺规作图，保留作图痕迹，不写做法）；‎ 参考小明的做法，解决以下问题：‎ ‎（3）将矩形沿直线折叠，求点的坐标；‎ ‎（4）将矩形沿直线折叠，点在边上（含端点），直接写出的取值范围。‎ 五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）‎ ‎23. 抛物线与轴交于点，，与轴交于点，其中点的坐标为.‎ ‎（1）求抛物线对应的函数表达式；‎ ‎（2）将（1）中的抛物线沿对称轴向上平移，使其顶点落在线段上，记该抛物线为，求抛物线 所对应的函数表达式；‎ ‎（3）将线段平移得到线段（的对应点为，的对应点为），使其经过（2）中所得抛物线 的顶点，且与抛物线另有一个交点，求点到直线的距离的取值范围。‎ O x y ‎24. 四边形是正方形，是等腰直角三角形，，，连接，为 的中点，连接，，。‎ ‎（1）如图24-1，若点在边的延长线上，直接写出与的位置关系及的值；‎ ‎（2）将图24-1中的绕点顺时针旋转至图24-2所示位置，请问（1）中所得的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；‎ ‎（3）将图24-1中的绕点顺时针旋转（），若，，当，，三 点共线时，求的长及的值。‎ A B C D 备用图 图24-2‎ A C D G E F B A C D G E F B 图24-1‎ ‎25. 定义1：在中，若顶点，，按逆时针方向排列，则规定它的面积为“有向面积”；若顶点 ‎，，按顺时针方向排列，则规定它的面积的相反数为的“有向面积”。“有向面积”用表示，‎ 图3‎ A B C D A B C 图2‎ A B C 图1‎ 例如图1中，，图2中，。‎ 定义2：在平面内任取一个和点（点不在的三边所在直线上），称有序数组（，‎ ‎，）为点关于的“面积坐标”，记作，例如图3中，菱形 的边长为2，，则，点关于的“面积坐标”为 ‎。‎ B C D A 在图3中，我们知道，利用“有向面积”，我们也可以把上式表示为：‎ ‎。‎ 应用新知：‎ ‎（1）如图4，正方形的边长为1，则 ，点关于的“面积坐标”是 ；‎ 探究发现：‎ ‎（2）在平面直角坐标系中，点，.‎ ‎①若点是第二象限内任意一点（不在直线上），设点关于的“面积坐标”为，‎ 试探究与之间有怎样的数量关系，并说明理由；‎ ‎②若点是第四象限内任意一点，请直接写出点关于的“面积坐标”（用表示）；‎ 解决问题：‎ ‎（3）在（2）的条件下，点，，点在抛物线上，求当的值 最小时，点的横坐标。‎