2020年中考数学试题分项版解析汇编（第01期）专题6 15页

专题6.2 数据分析 一、单选题 ‎1．一组数据2，1，2，5，3，2的众数是（　　）‎ A. 1 B. 2 C. 3 D. 5‎ ‎【来源】江苏省连云港市2018年中考数学试题 ‎【答案】B ‎【解析】详解：在数据2，1，2，5，3，2中2出现3次，次数最多，‎ 所以众数为2，‎ 故选：B．‎ 点睛：此题考查了众数，众数是一组数据中出现次数最多的数．‎ ‎2．甲、乙、丙、丁四名同学在一次投掷实心球训练中，在相同条件下各投掷10次，他们成绩的平均数与方差如下表：‎ 甲 乙 丙 丁 平均数（米）‎ ‎11.1‎ ‎11.1‎ ‎10.9‎ ‎10.9‎ 方差 ‎1.1‎ ‎1.2‎ ‎1.3‎ ‎1.4‎ 若要选一名成绩好且发挥稳定的同学参加比赛，则应该选择（ ）‎ A. 甲 B. 乙 C. 丙 D. 丁 ‎【来源】2018年甘肃省武威市（凉州区）中考数学试题 ‎【答案】A ‎【点评】考查平均数和方差的意义，方差越小，乘积越稳定.‎ ‎3．下列说法正确的是（ ）‎ A. 一组数据2，2，3，4，这组数据的中位数是2‎ B. 了解一批灯泡的使用寿命的情况，适合抽样调查 15‎ C. 小明的三次数学成绩是126分，130分，136分，则小明这三次成绩的平均数是131分 D. 某日最高气温是，最低气温是，则该日气温的极差是 ‎【来源】江苏省扬州市2018年中考数学试题 ‎【答案】B 点睛：此题主要考查了中位数、抽样调查的意义和平均数的求法、极差，正确把握相关定义是解题关键．‎ ‎4．一组数据2，4，6，4，8的中位数为（   ）‎ A. 2 B. 4 C. 6 D. 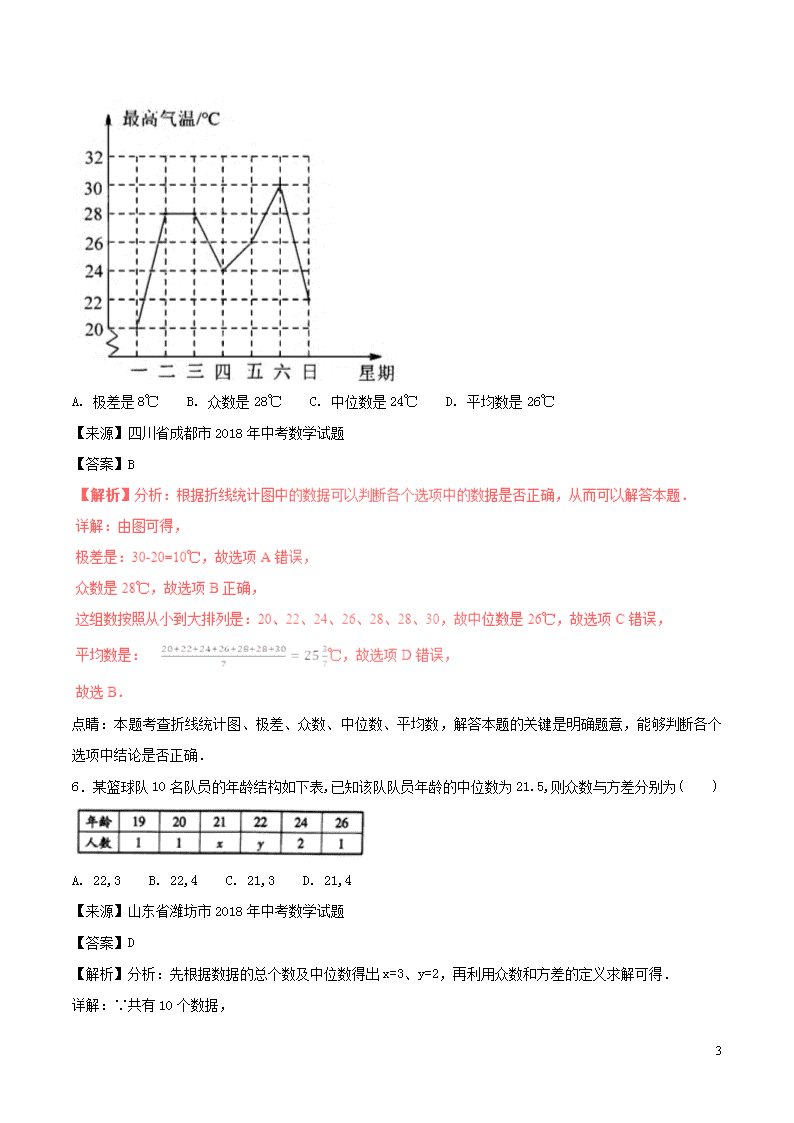8‎ ‎【来源】江苏省盐城市2018年中考数学试题 ‎【答案】B ‎【解析】分析：找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数．‎ 详解：一共5个数据，从小到大排列此数据为：2，4，4，6，8， 故这组数据的中位数是4． 故选：B．‎ 点睛：本题属于基础题，考查了确定一组数据的中位数的能力．注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数．‎ ‎5．如图是成都市某周内日最高气温的折线统计图，关于这7天的日最高气温的说法正确的是（ ）‎ 15‎ A. 极差是8℃ B. 众数是28℃ C. 中位数是24℃ D. 平均数是26℃‎ ‎【来源】四川省成都市2018年中考数学试题 ‎【答案】B 点睛：本题考查折线统计图、极差、众数、中位数、平均数，解答本题的关键是明确题意，能够判断各个选项中结论是否正确．‎ ‎6．某篮球队10名队员的年龄结构如下表,已知该队队员年龄的中位数为21.5,则众数与方差分别为( )‎ A. 22,3 B. 22,4 C. 21,3 D. 21,4‎ ‎【来源】山东省潍坊市2018年中考数学试题 ‎【答案】D ‎【解析】分析：先根据数据的总个数及中位数得出x=3、y=2，再利用众数和方差的定义求解可得．‎ 详解：∵共有10个数据，‎ 15‎ ‎∴x+y=5，‎ 又该队队员年龄的中位数为21.5，即，‎ ‎∴x=3、y=2，‎ 则这组数据的众数为21，平均数为=22，‎ 所以方差为×[（19-22）2+（20-22）2+3×（21-22）2+2×（22-22）2+2×（24-22）2+（26-22）2]=4，‎ 故选D．‎ 点睛：本题主要考查中位数、众数、方差，解题的关键是根据中位数的定义得出x、y的值及方差的计算公式． ‎ ‎7．学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛，在选拔过程中，每人射击次，计算他们的平均成绩及方差如表，请你根据表中的数据选一人参加比赛，最适合的人选是__________．‎ 选手 甲 乙 平均数（环）‎ 方差 ‎【来源】贵州省安顺市2018年中考数学试题 ‎【答案】乙 点睛：本题考查了方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．‎ ‎8．某校九年级“诗歌大会”比赛中，各班代表队得分如下（单位：分）：9，7，8，7，9，7，6，则各代表队得分的中位数是（    ）‎ A. 9分 B. 8分 C. 7分 D. 6分 ‎【来源】浙江省温州市2018年中考数学试卷 ‎【答案】C ‎【解析】分析: 根据中位数的定义，首先将这组数据按从小到大的顺序排列起来，由于这组数据共有7‎ 15‎ 个，故处于最中间位置的数就是第四个，从而得出答案.‎ 详解: 将这组数据按从小到大排列为：6＜7＜7＜7＜8＜9＜9，故中位数为 ：7分，‎ 故答案为：C.‎ 点睛: 本题主要考查中位数，解题的关键是掌握中位数的定义：将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数.‎ ‎9．下列数据：，则这组数据的众数和极差是( )‎ A. B. C. D. ‎ ‎【来源】广东省深圳市2018年中考数学试题 ‎【答案】A ‎【点睛】本题考查了众数和极差的定义，熟练掌握众数和极差的定义是解题的关键.‎ ‎10．某排球队名场上队员的身高（单位：）是：，，，，，.现用一名身高为的队员换下场上身高为的队员，与换人前相比，场上队员的身高（ ）‎ A. 平均数变小，方差变小 B. 平均数变小，方差变大 C. 平均数变大，方差变小 D. 平均数变大，方差变大 ‎【来源】江苏省南京市2018年中考数学试卷 ‎【答案】A ‎【解析】分析：根据平均数的计算公式进行计算即可,根据方差公式先分别计算出甲和乙的方差，再根据方差的意义即可得出答案.‎ 详解：换人前6名队员身高的平均数为==188，‎ 方差为 S2==；‎ 换人后6名队员身高的平均数为==187，‎ 方差为 15‎ S2==‎ ‎∵188＞187，＞，‎ ‎∴平均数变小，方差变小，‎ 故选：A.‎ 点睛：本题考查了平均数与方差的定义：一般地设n个数据，x1，x2，…xn的平均数为，则方差S2=[（x1-）2+（x2-）2+…+（xn-）2]，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立.‎ ‎11．一组数据-3，2，2，0，2，1的众数是（ ）‎ A. -3 B. 2 C. 0 D. 1‎ ‎【来源】湖南省娄底市2018年中考数学试题 ‎【答案】B ‎【点睛】本题考查了众数的定义，熟练掌握众数的定义是解题的关键.‎ ‎12．下列说法正确的是（ ）‎ A. 了解“孝感市初中生每天课外阅读书籍时间的情况”最适合的调查方式是全面调查 B. 甲乙两人跳绳各10次，其成绩的平均数相等，，则甲的成绩比乙稳定 C. 三张分别画有菱形，等边三角形，圆的卡片，从中随机抽取一张，恰好抽到中心对称图形卡片的概率是 D. “任意画一个三角形，其内角和是”这一事件是不可能事件 ‎【来源】湖北省孝感市2018年中考数学试题 ‎【答案】D ‎【解析】分析：根据随机事件的概念以及概率的意义结合选项可得答案．‎ 详解：A、了解“孝感市初中生每天课外阅读书籍时间的情况”最适合的调查方式是抽样调查，此选项错误；‎ B、甲乙两人跳绳各10次，其成绩的平均数相等，S甲2＞S乙2，则乙的成绩比甲稳定，此选项错误；‎ C、三张分别画有菱形，等边三角形，圆的卡片，从中随机抽取一张，恰好抽到中心对称图形卡片的概率是 15‎ ‎，此选项错误；‎ D、“任意画一个三角形，其内角和是360°”这一事件是不可能事件，此选项正确.‎ 故选：D．‎ 点睛：此题主要考查了概率的意义，关键是弄清随机事件和必然事件的概念的区别．‎ ‎13．已知一组数据：6，2，8，，7，它们的平均数是6．则这组数据的中位数是（ ）‎ A. 7 B. 6 C. 5 D. 4‎ ‎【来源】山东省德州市2018年中考数学试题 ‎【答案】A 点睛：本题考查了中位数和平均数的知识，将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数；如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数；平均数是指在一组数据中所有数据之和再除以数据的个数．‎ ‎14．为考察两名实习工人的工作情况，质检部将他们工作第一周每天生产合格产品的个数整理成甲，乙两组数据，如下表：‎ 甲 ‎2‎ ‎6‎ ‎7‎ ‎7‎ ‎8‎ 乙 ‎2‎ ‎3‎ ‎4‎ ‎8‎ ‎8‎ 关于以上数据，说法正确的是（ ）‎ A. 甲、乙的众数相同 B. 甲、乙的中位数相同 C. 甲的平均数小于乙的平均数 D. 甲的方差小于乙的方差 ‎【来源】安徽省2018年中考数学试题 ‎【答案】D ‎【解析】【分析】分别根据众数、中位数、平均数、方差的定义进行求解后进行判断即可得.‎ ‎【详解】甲：数据7出现了2次，次数最多，所以众数为7，‎ 排序后最中间的数是7，所以中位数是7，‎ ‎，‎ 15‎ ‎=4.4，‎ 乙：数据8出现了2次，次数最多，所以众数为8，‎ 排序后最中间的数是4，所以中位数是4，‎ ‎，‎ ‎=6.4，‎ 所以只有D选项正确，‎ 故选D.‎ ‎【点睛】本题考查了众数、中位数、平均数、方差，熟练掌握相关定义及求解方法是解题的关键. ‎ ‎15．某中学九年级二班六级的8名同学在一次排球垫球测试中的成绩如下（单位：个）‎ ‎35 38 42 44 40 47 45 45‎ 则这组数据的中位数、平均数分别是（ ）‎ A. 42、42 B. 43、42 C. 43、43 D. 44、43‎ ‎【来源】山东省泰安市2018年中考数学试题 ‎【答案】B 点睛：本题考查的是中位数的确定、算术平均数的计算，掌握中位数的概念、算术平均数的计算公式是解题的关键．‎ ‎16．如果一组数据6、7、x、9、5的平均数是2x，那么这组数据的方差为（　　）‎ A. 4 B. 3 C. 2 D. 1‎ ‎【来源】山东省滨州市2018年中考数学试题 ‎【答案】A ‎【解析】分析：先根据平均数的定义确定出x的值，再根据方差公式进行计算即可求出答案．‎ 详解：根据题意，得：=2x 解得：x=3，‎ 则这组数据为6、7、3、9、5，其平均数是6，‎ 15‎ 所以这组数据的方差为 [（6﹣6）2+（7﹣6）2+（3﹣6）2+（9﹣6）2+（5﹣6）2]=4，‎ 故选A．‎ 点睛：此题考查了平均数和方差的定义．平均数是所有数据的和除以数据的个数．方差是一组数据中各数据与它们的平均数的差的平方的平均数．‎ 二、填空题 ‎17．一组数据：2,5,3,1,6，则这组数据的中位数是________.‎ ‎【来源】江苏省宿迁市2018年中考数学试卷 ‎【答案】3‎ ‎【点睛】本题考查了中位数的定义，中位数是将一组数据从小到大或从大到小排列，处于最中间（中间两数的平均数）的数即为这组数据的中位数.‎ ‎18．如图是我国2013～2017年国内生产总值增长速度统计图，则这5年增长速度的众数是_____．‎ ‎【来源】浙江省金华市2018年中考数学试题 ‎【答案】6.9%．‎ ‎【解析】分析：根据众数的概念判断即可．‎ 详解：这5年增长速度分别是7.8%、7.3%、6.9%、6.7%、6.9%，‎ 则这5年增长速度的众数是6.9%，‎ 故答案为：6.9%．‎ 点睛：本题考查的是众数的确定，掌握一组数据中出现次数最多的数据叫做众数是解题的关键．‎ ‎19．一组数据1，3，2，7，x，2，3的平均数是3，则该组数据的众数为________．‎ 15‎ ‎【来源】浙江省温州市2018年中考数学试卷 ‎【答案】3‎ 点睛: 本题考查的是平均数和众数的概念．注意一组数据的众数可能不只一个.‎ ‎20．某校拟招聘一名优秀数学教师，现有甲、乙、丙三名教师入围，三名教师师笔试、面试成绩如右表所示，综合成绩按照笔试占60%、面试占40%进行计算，学校录取综合成绩得分最高者，则被录取教师的综合成绩为分_____． ‎ ‎【来源】四川省宜宾市2018年中考数学试题 ‎【答案】78.8分．‎ ‎【解析】分析：根据题意先算出甲、乙、丙三人的综合成绩，再进行比较，即可得出答案．‎ 详解：∵甲的综合成绩为80×60%+76×40%=78.4（分），‎ 乙的综合成绩为82×60%+74×40%=78.8（分），‎ 丙的综合成绩为78×60%+78×40%=78（分），‎ ‎∴被录取的教师为乙，其综合成绩为78.8分，‎ 故答案为：78.8分．‎ 点睛：本题考查了加权平均数的计算公式，注意，计算平均数时按60%和40%进行计算．‎ ‎21．春节期间，重庆某著名旅游景点成为热门景点，大量游客慕名前往，市旅游局统计了春节期间5天的游客数量，绘制了如图所示的折线统计图，则这五天游客数量的中位数为______.‎ 15‎ ‎【来源】【全国省级联考】2018年重庆市中考数学试卷（A卷）‎ ‎【答案】23.4‎ ‎【点睛】本题考查了中位数的定义，熟知“中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（或最中间两个数的平均数）”是解题的关键. ‎ 三、解答题 ‎22．4月23日是世界读书日，习近平总书记说：“读书可以让人保持思想活力，让人得到智慧启发，让人滋养浩然之气。”某校响应号召，鼓励师生利用课余时间广泛阅读，该校文学社为了解学生课外阅读的情况，抽样调查了部分学生每周用于课外阅读的时间，过程如下：‎ 收集数据 从学校随机抽取20名学生，进行了每周用于课外阅读时间的调查，数据如下(单位：min):‎ ‎ 30 60 81 50 40 110 130 146 90 100‎ ‎ 60 81 120 140 70 81 10 20 100 81‎ 整理数据 按如下分段整理样本数据并补全表格：‎ 课外阅读时间(min)‎ 等级 D C B A 人数 ‎3‎ ‎8‎ 分析数据 补全下列表格中的统计量：‎ 平均数 中位数 众数 15‎ ‎80‎ 得出结论 ‎ ‎ (1)用样本中的统计量估计该校学生每周用于课外阅读时间的情况等级为 ；‎ ‎ (2)如果该校现有学生400人，估计等级为“”的学生有多少名？‎ ‎ (3)假设平均阅读一本课外书的时间为160分钟，请你选择一种统计量估计该校学生每人一年 (按52周计算)平均阅读多少本课外书？‎ ‎【来源】江西省2018年中等学校招生考试数学试题 ‎【答案】（1）填表见解析；（2）160名；（3）平均数；26本.‎ ‎【详解】整理数据 按如下分段整理样本数据并补全表格：‎ 课外阅读时间(min)‎ 等级 D C B A 人数 ‎3‎ ‎5‎ ‎8‎ ‎4‎ 分析数据 补全下列表格中的统计量：‎ 平均数 中位数 众数 ‎80‎ ‎81‎ ‎81‎ 得出结论 ‎（1）观察统计量表格可以估计该校学生每周用于课外阅读时间的情况等级B ，‎ 故答案为：B；‎ ‎（2） 8÷20×400=160 ∴该校等级为“”的学生有160名； ‎ ‎（3） 选统计量：平均数 15‎ ‎80×52÷160=26 ，‎ ‎∴该校学生每人一年平均阅读26本课外书.‎ ‎【点睛】本题考查了中位数、众数、平均数、统计表、用样本估计总体等知识，熟练掌握各统计量的求解方法是关键.‎ ‎23．随机抽取某理发店一周的营业额如下表（单位：元）：‎ 星期一 星期二 星期三 星期四 星期五 星期六 星期日 合计 ‎540‎ ‎680‎ ‎760‎ ‎640‎ ‎960‎ ‎2200‎ ‎1780‎ ‎7560‎ ‎（1）求该店本周的日平均营业额.‎ ‎（2）如果用该店本周星期一到星期五的日平均营业额估计当月的营业总额，你认为是否合理？如果合理，请说明理由；如果不合理，请设计一个方案，并估计该店当月（按30天计算）的营业总额.‎ ‎【来源】江苏省南京市2018年中考数学试卷 ‎【答案】（1）1080元；（2）不合理.‎ 点睛：此题主要考查了一组数据平均数的求法，解决本题的关键是正确的从表中整理出所有数据，并进行正确的计算和分析. ‎ ‎24．某厂为了检验甲、乙两车间生产的同一款新产品的合格情况（尺寸范围为的产品为合格），随机各抽取了20个样品进行检测，过程如下：‎ 收集数据（单位：）：‎ 甲车间：‎ ‎168，175，180，185，172，189，185，182，185，174，192，180，185，178，173，185，169，187，176，180.‎ 乙车间：‎ 15‎ ‎186，180，189，183，176，173，178，167，180，175，178，182，180，179，185，180，184，182，180，183.‎ 整理数据：‎ 分析数据：‎ 车间 平均数 众数 中位数 方差 甲车间 ‎180‎ ‎185‎ ‎180‎ ‎43.1‎ 乙车间 ‎180‎ ‎180‎ ‎180‎ ‎22.6‎ 应用数据：‎ ‎（1）计算甲车间样品的合格率.‎ ‎（2）估计乙车间生产的1000个该款新产品中合格产品有多少个？‎ ‎（3）结合上述数据信息，请判断哪个车间生产的新产品更好，并说明理由.‎ ‎【来源】2018年浙江省舟山市中考数学试题 ‎【答案】（1）甲车间样品的合格率为；（2）乙车间的合格产品数为750个；（3）见解析.‎ ‎（3）①从样品合格率看，乙车间合格率比甲车间高，所以乙车间生产的新产品更好.‎ 15‎ ‎②从样品的方差看，甲、乙平均数相等，且均在合格范围内，而乙的方差小于甲的方差，说明乙比甲稳定，所以乙车间生产的新产品更好.‎ ‎【点评】考查用样本估计总体，数据的分析，方差等，注意方差越小，越稳定. ‎ 15‎