上海市浦东新区中考数学一模数学试卷含答案 9页

浦东新区2015-2016学年第一学期初三教学质量检测 数学试卷 一、选择题：（本大题共6小题，每题4分，满分24分）‎ ‎1.如果两个相似三角形对应边之比是1:4，那么它们的对应边上的中线之比是（ ）‎ A. 1:2 B. 1:‎4 C. 1:8 D. 1:16‎ ‎2.在Rt△ABC中，∠C=90°，AB=5，BC=4，则sinA的值为（ ）‎ A. B. C. D. ‎ ‎3.如图，点D、E分别在AB、AC上，以下能推得DE//BC的条件是（ ）‎ A. AD:AB=DE:BC； B. AD:DB=DE:BC； [来源:学,科,网Z,X,X,K]‎ y C. AD:DB=AE:EC； D. AE:AC=AD:DB.‎ ‎4.已知二次函数y=ax2+bx+c的图像如图所示，那么a、b、c的符号为（ ）‎ x o A. a＜0，b＜0，c＞0； B. a＜0，b＜0，c＜0；‎ C. a＞0，b＞0，c＞0； D. a＞0，b＞0，c＜0.‎ ‎5.如图，Rt△ABC中，∠ACB=90°，CD⊥AB于点D，下列结论中错误的是（ ）‎ A. AC2=AD·AB； B. CD2=CA·CB；‎ C. CD2=AD·DB； D. BC2=BD·BA.‎ ‎6.下列命题是真命题的是（ ）‎ A. 有一个角相等的两个等腰三角形相似；‎ B. 两边对应成比例且有一个角相等的两个三角形相似；‎ C. 四个内角都对应相等的两个四边形相似；‎ D. 斜边和一条直角边对应成比例的两个直角三角形相似. 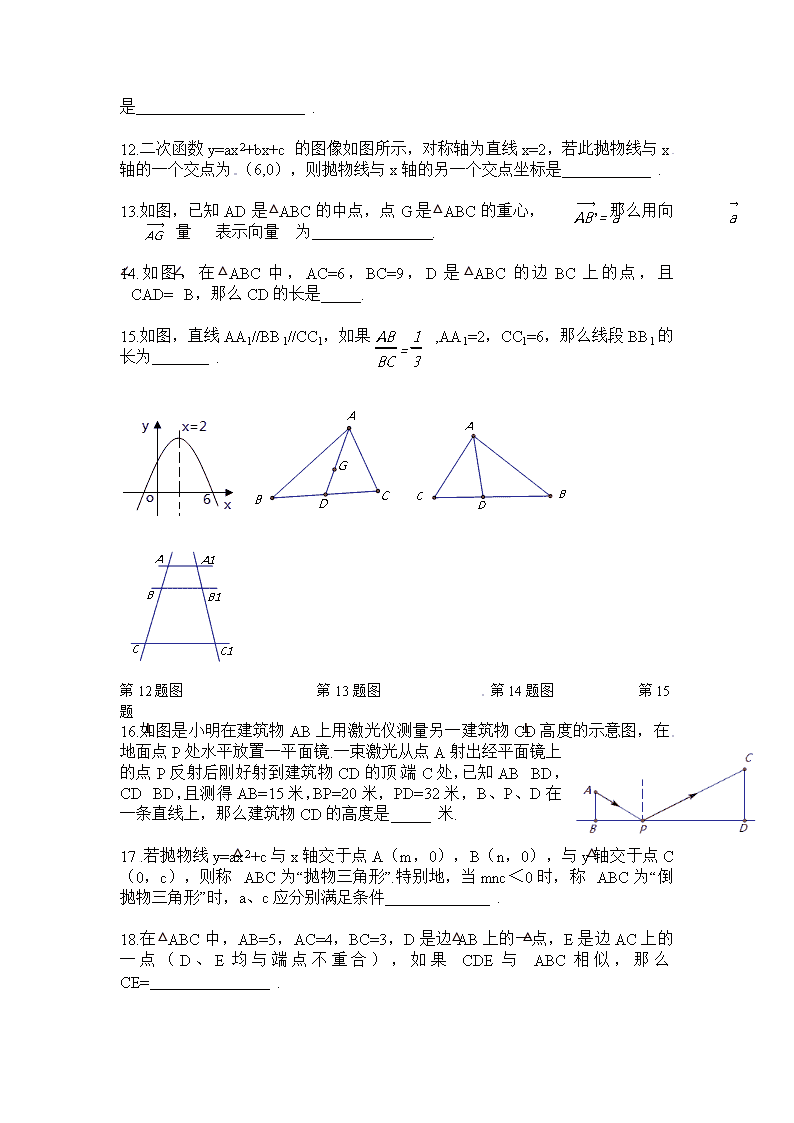‎ 二、填空题（本大题共12小题，每题4分，满分48分）‎ ‎7.已知 ，那么 .‎ ‎8.计算： .‎ ‎9.上海与杭州的实际距离约200千米，在比例尺1:5000 000的地图上，上海与杭州的图上距离约 厘米.‎ ‎10.某滑雪运动员沿着坡比为1： 的斜坡向下滑行了‎100m，则运动员下降的垂直高度是 米.‎ ‎11.将抛物线y=(x+1)2向下平移2个单位，得到新抛物线的函数解析式 是 .‎ ‎12.二次函数y=ax2+bx+c 的图像如图所示，对称轴为直线x=2，若此抛物线与x轴的一个交点为（6,0），则抛物线与x轴的另一个交点坐标是 .‎ ‎13.如图，已知AD是△ABC的中点，点G是△ABC的重心， ，那么用向量 表示向量 为 . ‎ ‎14.如图，在△ABC中，AC=6，BC=9，D是△ABC的边BC上的点，且∠CAD=∠B，那么CD的长是 .‎ ‎15.如图，直线AA1//BB1//CC1，如果 ,AA1=2，CC1=6，那么线段BB1的长为 .‎ ‎ ‎ 第12题图 第13题图 第14题图 第15题 ‎16.如图是小明在建筑物AB上用激光仪测量另一建筑物CD高度的示意图，在地面点P处水平放置一平面镜.一束激光从点A射出经平面镜上的点P反射后刚好射到建筑物CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=‎15米，BP=‎20米，PD=‎32米，B、P、D在一条直线上，那么建筑物CD的高度是 米.‎ ‎17.若抛物线y=ax2+c与x轴交于点A（m，0），B（n，0），与y轴交于点C（0，c），则称△ABC为“抛物三角形”.特别地，当mnc＜0时，称△ABC为“倒抛物三角形”时，a、c应分别满足条件 .‎ ‎18.在△ABC中，AB=5，AC=4，BC=3，D是边AB上的一点，E是边AC上的一点（D、E均与端点不重合），如果△CDE与△ABC相似，那么CE= .‎ 三、解答题（本大题共7小题，满分78分）‎ ‎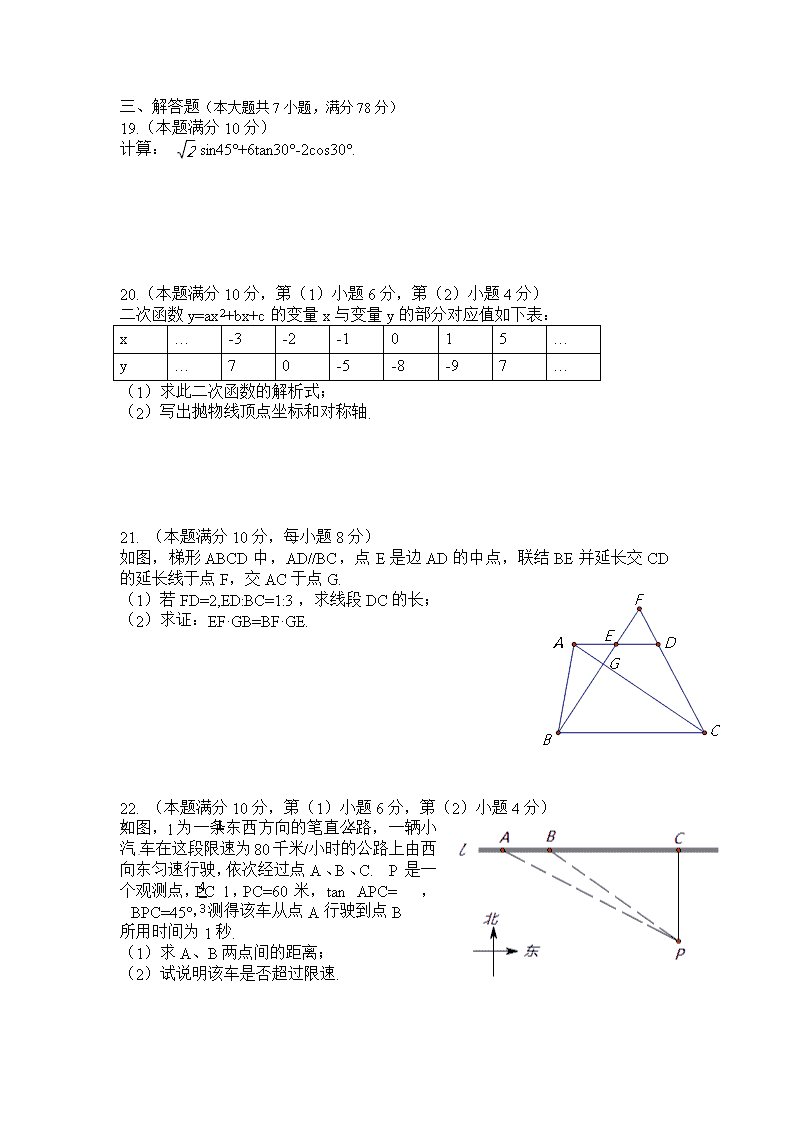19.（本题满分10分）‎ 计算： sin45°+6tan30°-2cos30°.‎ ‎20.（本题满分10分，第（1）小题6分，第（2）小题4分）‎ 二次函数y=ax2+bx+c的变量x与变量y的部分对应值如下表：‎ x ‎…‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎5‎ ‎…‎ y[来源:学,科,网Z,X,X,K]‎ ‎…‎ ‎7‎ ‎0‎ ‎-5‎ ‎-8‎ ‎-9‎ ‎7‎ ‎…‎ ‎（1）求此二次函数的解析式；‎ ‎（2）写出抛物线顶点坐标和对称轴.‎ ‎21. （本题满分10分，每小题8分）‎ 如图，梯形ABCD中，AD//BC，点E是边AD的中点，联结BE并延长交CD的延长线于点F，交AC于点G.‎ ‎（1）若FD=2,ED:BC=1:3，求线段DC的长；‎ ‎（2）求证：EF·GB=BF·GE.‎ ‎[来源:学科网ZXXK]‎ ‎22. （本题满分10分，第（1）小题6分，第（2）小题4分）‎ 如图，l为一条东西方向的笔直公路，一辆小汽车在这段限速为80千米/小时的公路上由西向东匀速行驶，依次经过点A、B、C. P是一个观测点，PC⊥l，PC=‎60米，tan∠APC= ，∠BPC=45°，测得该车从点A行驶到点B 所用时间为1秒.‎ ‎（1）求A、B两点间的距离；‎ ‎（2）试说明该车是否超过限速.‎ ‎23. （本题满分12分，每小题6分）‎ 如图，在△ABC中，D是BC边的中点，DE⊥BC交AB于点E，AD=AC，EC交AD于点F.‎ ‎（1）求证：△ABC∽△FCD；‎ ‎（2）求证：FC=3EF.‎ ‎24. （本题满分12分，每小题4分）‎ 如图，抛物线y=ax2+2ax+c（a＞0）与x轴交于A（-3,0）、B两点（A在B的左侧），与y轴交于点 C（0，-3），抛物线的顶点为M.‎ ‎（1）求a、c的值；‎ ‎（2）求tan∠MAC的值；‎ ‎（3）若点P是线段AC上一个动点，联结OP.问：是否存在点P，使得以点O、C、P为顶点的三角形与△ABC相似？若存在，求出P点的坐标；若不存在，请说明理由.‎ ‎25. （本题满分14分，第（1）（2）小题，每题5分，第（3）小题4分）‎ 如图，在边长为6的正方形ABCD中，点E为AD边上的一个动点（与点A、D不重合），∠EBM=45°，BE交对角线AC于点F，BM交对角线AC于点G，交CD于点M.‎ ‎（1）如图1，联结BD，求证：△DEB∽△CGB，并写出DE:CG的值；‎ ‎（2）联结EG，如图2，若设AE=x，EG=y，求y关于x的函数解析式，并写出函数的定义域；‎ ‎（3）当M为边DC的三等分点时，求S△EGF的面积.‎ ‎ ‎ ‎ 备用图 ‎21、‎ ‎22、‎ ‎23、‎ ‎24、‎ ‎25、‎