2009年青海省西宁市中考数学试题及答案 9页

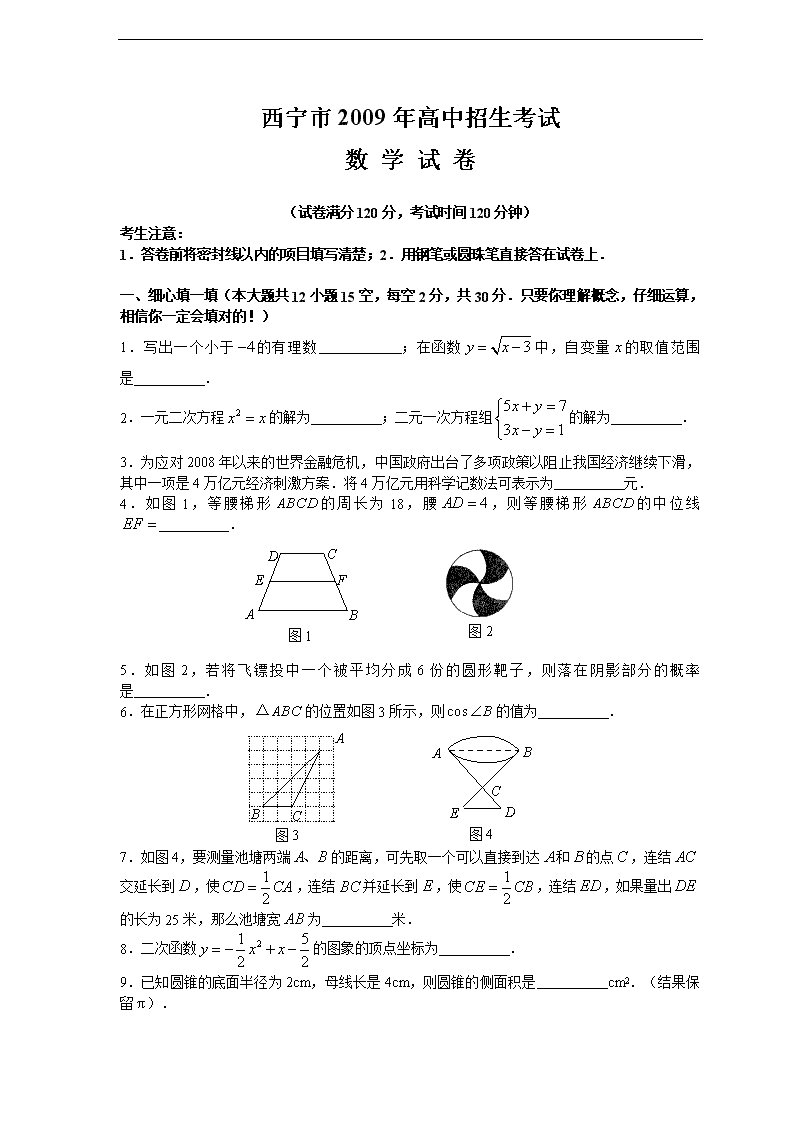
西宁市2009年高中招生考试 数 学 试 卷 ‎（试卷满分120分，考试时间120分钟）‎ 考生注意：‎ ‎1．答卷前将密封线以内的项目填写清楚；2．用钢笔或圆珠笔直接答在试卷上．‎ 一、细心填一填（本大题共12小题15空，每空2分，共30分．只要你理解概念，仔细运算，相信你一定会填对的！）‎ ‎1．写出一个小于的有理数 ；在函数中，自变量的取值范围是 ．‎ ‎2．一元二次方程的解为 ；二元一次方程组的解为 ．‎ ‎3．为应对2008年以来的世界金融危机，中国政府出台了多项政策以阻止我国经济继续下滑，其中一项是4万亿元经济刺激方案．将4万亿元用科学记数法可表示为 元．‎ ‎4．如图1，等腰梯形的周长为18，腰，则等腰梯形的中位线 ．‎ 图2‎ D C F E A B 图1‎ ‎5．如图2，若将飞镖投中一个被平均分成6份的圆形靶子，则落在阴影部分的概率是 ．‎ ‎6．在正方形网格中，的位置如图3所示，则的值为 ．‎ A B D C E 图4‎ A C B 图3‎ ‎7．如图4，要测量池塘两端的距离，可先取一个可以直接到达和的点，连结交延长到，使，连结并延长到，使，连结，如果量出的长为‎25米，那么池塘宽为 米．‎ ‎8．二次函数的图象的顶点坐标为 ．‎ ‎9．已知圆锥的底面半径为‎2cm，母线长是‎4cm，则圆锥的侧面积是 cm2．（结果保留）．‎ ‎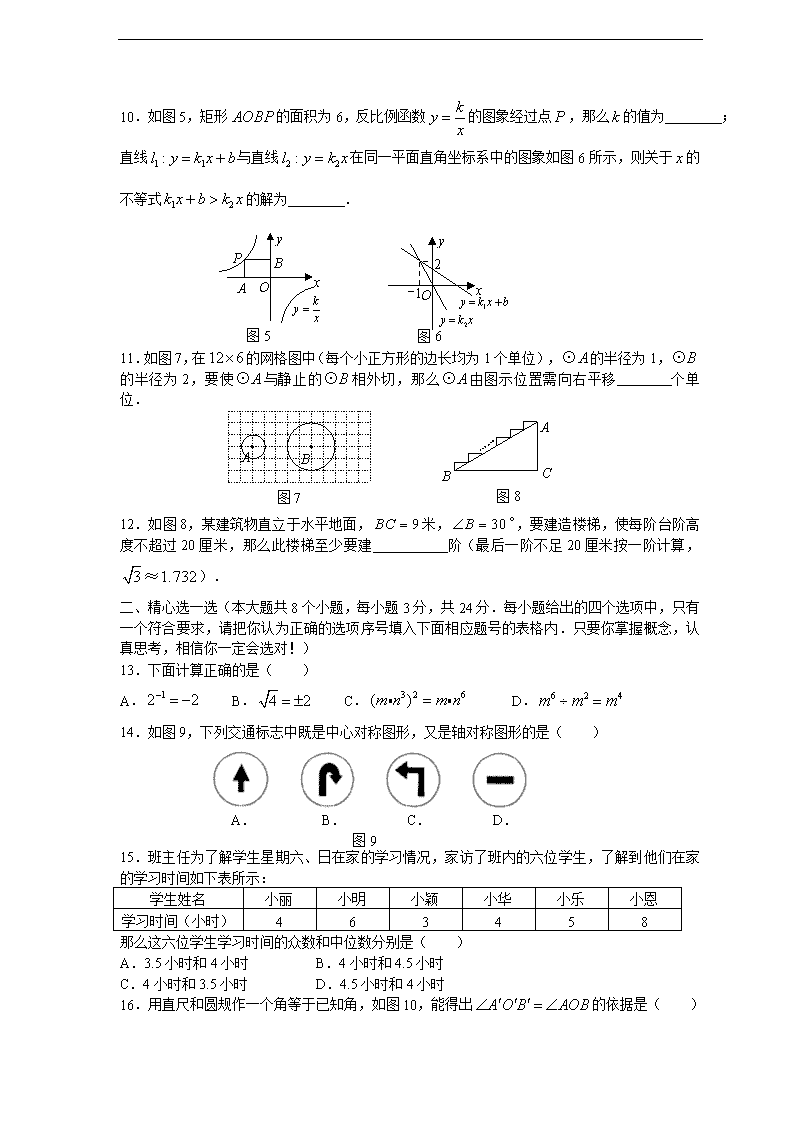10．如图5，矩形的面积为6，反比例函数的图象经过点，那么的值为 ；直线与直线在同一平面直角坐标系中的图象如图6所示，则关于的不等式的解为 ．‎ O x y 图6‎ ‎2‎ ‎-1‎ B O A P x y 图5‎ ‎11．如图7，在的网格图中（每个小正方形的边长均为1个单位），的半径为1，的半径为2，要使与静止的相外切，那么由图示位置需向右平移 个单位．‎ A B C 图8‎ A B 图7‎ ‎12．如图8，某建筑物直立于水平地面，米，，要建造楼梯，使每阶台阶高度不超过20厘米，那么此楼梯至少要建 阶（最后一阶不足20厘米按一阶计算，）．‎ 二、精心选一选（本大题共8个小题，每小题3分，共24分．每小题给出的四个选项中，只有一个符合要求，请把你认为正确的选项序号填入下面相应题号的表格内．只要你掌握概念，认真思考，相信你一定会选对！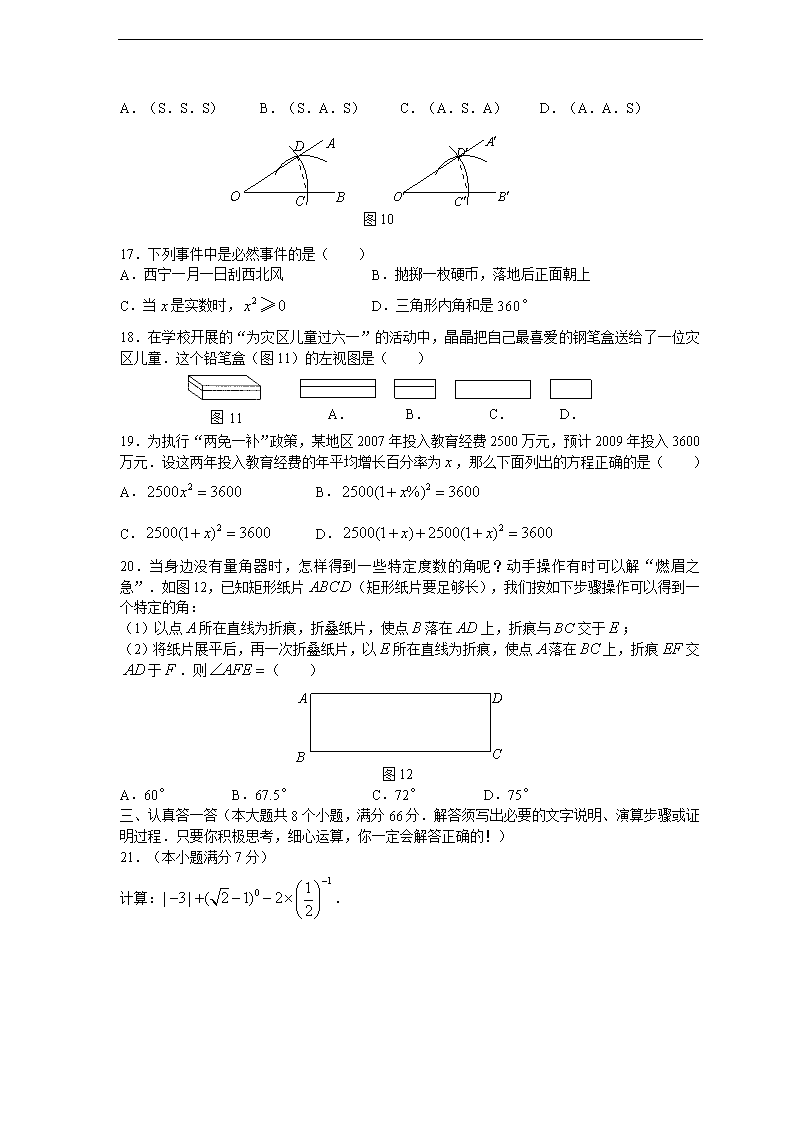）‎ ‎13．下面计算正确的是（ ）‎ A． B． C． D．‎ ‎14．如图9，下列交通标志中既是中心对称图形，又是轴对称图形的是（ ）‎ A．‎ B．‎ C．‎ D．‎ 图9‎ ‎15．班主任为了解学生星期六、日在家的学习情况，家访了班内的六位学生，了解到他们在家的学习时间如下表所示：‎ 学生姓名 小丽 小明 小颖 小华 小乐 小恩 学习时间（小时）‎ ‎4‎ ‎6‎ ‎3‎ ‎4‎ ‎5‎ ‎8‎ 那么这六位学生学习时间的众数和中位数分别是（ ）‎ A．3.5小时和4小时 B．4小时和4.5小时 C．4小时和3.5小时 D．4.5小时和4小时 ‎16．用直尺和圆规作一个角等于已知角，如图10，能得出的依据是（ ）‎ A．（S．S．S） B．（S．A．S） C．（A．S．A） D．（A．A．S）‎ D A B C O 图10‎ ‎17．下列事件中是必然事件的是（ ）‎ A．西宁一月一日刮西北风 B．抛掷一枚硬币，落地后正面朝上 C．当是实数时， D．三角形内角和是 ‎18．在学校开展的“为灾区儿童过六一”的活动中，晶晶把自己最喜爱的钢笔盒送给了一位灾区儿童．这个铅笔盒（图11）的左视图是（ ）‎ 图11１‎ A．‎ B．‎ C．‎ D．‎ ‎19．为执行“两免一补”政策，某地区2007年投入教育经费2500万元，预计2009年投入3600万元．设这两年投入教育经费的年平均增长百分率为，那么下面列出的方程正确的是（ ）‎ A． B．‎ C． D．‎ ‎20．当身边没有量角器时，怎样得到一些特定度数的角呢？动手操作有时可以解“燃眉之急”．如图12，已知矩形纸片（矩形纸片要足够长），我们按如下步骤操作可以得到一个特定的角：‎ ‎（1）以点所在直线为折痕，折叠纸片，使点落在上，折痕与交于；‎ ‎（2）将纸片展平后，再一次折叠纸片，以所在直线为折痕，使点落在上，折痕交于．则（ ）‎ A B C D 图12‎ A．60° B．67.5° C．72° D．75°‎ 三、认真答一答（本大题共8个小题，满分66分．解答须写出必要的文字说明、演算步骤或证明过程．只要你积极思考，细心运算，你一定会解答正确的！）‎ ‎21．（本小题满分7分）‎ 计算：．‎ ‎22．（本小题满分7分）‎ 请从下列三个代数式中任选两个（一个作为分子，一个作为分母）构造一个分式，并化简该分式．‎ ‎ ‎ 然后请你自选一个合理的数代入求值．‎ ‎23．（本小题满分7分）‎ 如图13，在中，‎ ‎（1）尺规作图（不写作法，保留作图痕迹）：作的平分线交于；在线段上截取；连结．‎ ‎（2）求证：四边形是菱形．‎ A D B C 图13‎ ‎24．（本小题满分8分）‎ 阅读下列材料并填空：‎ ‎（1）探究：平面上有个点（）且任意3个点不在同一条直线上，经过每两点画一条直线，一共能画多少条直线？‎ 我们知道，两点确定一条直线．平面上有2个点时，可以画条直线，平面内有3个点时，一共可以画条直线，平面上有4个点时，一共可以画条直线，平面内有5个点时，一共可以画 条直线，……平面内有个点时，一共可以画 条直线．‎ ‎（2）迁移：某足球比赛中有个球队（）进行单循环比赛（每两队之间必须比赛一场），一共要进行多少场比赛？‎ 有2个球队时，要进行场比赛，有3个球队时，要进行场比赛，有4个球队时，要进行 场比赛，……那么有20个球队时，要进行 场比赛．‎ ‎25．（本小题满分8分）‎ 已知：如图14，为的直径，，交于，于．‎ ‎（1）请判断与的位置关系，并证明；‎ 图14‎ O A B D C E ‎（2）连结，若的半径为，，求的长．‎ ‎26．（本小题满分8分）‎ ‎《西海都市报》（‎2009年05月21日）文章《创卫让西宁焕发出勃勃生机》报道说：“西宁创建卫生城市已到了关键阶段，西宁处处焕发出勃勃生机．”省城西宁，无论是市容环境，还是市民意识，都发生了可喜的变化．西宁市教育局对全市约11000名九年级学生就西宁创建卫生城市知识的了解情况进行了问卷调查．现随机抽取了部分学生的答卷进行统计分析，然后按“很好”、“较好”、“一般”、“较差”四类汇总分析，并绘制了扇形统计图（如图15）和条形统计图（如图16）．请你根据图中信息回答下列问题：‎ ‎100‎ ‎80‎ ‎60‎ ‎40‎ ‎20‎ 很好 较好 一般 较差 了解情况 人数 图16‎ 很好25%‎ 一般 较差5%‎ 较好50%‎ 图15‎ ‎（1）本次问卷调查的样本容量是 ；‎ ‎（2）扇形统计图中，圆心角 ；‎ ‎（3）补全条形统计图；‎ ‎（4）根据以上信息，请提出一条合理化的创卫建议： ．‎ ‎27．（本小题满分9分）‎ 已知一只口袋中放有只白球和只红球，这两种球除颜色以外没有任何区别．袋中的球已经搅匀．蒙上眼睛从袋中取一只球，取出白球的概率是．‎ ‎（1）试写出与的函数关系式；‎ ‎（2）当时，第一次任意摸一个球（不放回），第二次再摸一个球，请用画树状图或列表法，求两次摸到都是白球的概率．‎ ‎28．（本小题满分12分）‎ 已知是一张矩形纸片，．‎ ‎（1）如图17，在上取一点，使得与关于所在直线对称，点恰好在边上，且的面积为‎24cm2，求的长；‎ ‎（2）如图18．以为原点，所在直线分别为轴、轴建立平面直角坐标系．求对称轴所在直线的函数关系式；‎ ‎（3）作交于点，若抛物线过点，求这条抛物线所对应的函数关系式．‎ C B O A M 图18‎ x y G C B O A M 图17‎ 参考答案：‎ 一、细心填一填 ‎1. -5、-6等；x≥3 2. 0，1；‎ ‎3. 4×1012 4. 5‎ ‎5. 6. ‎ ‎7. 50 8. （1，－2）‎ ‎9. 8π 10. －6；x＞－1‎ ‎11. 2、4、6、8 12. 26‎ 二、精心选一选 ‎13－16 DDBA 17－20 CBCB 三、认真答一答 ‎21.解：原式=3＋1－2×2＝0.‎ ‎22.解：略. 答案不唯一。‎ ‎23.解：（1）作图略。‎ ‎（2）证明：∵ABCD是平行四边形，‎ A D B C 图13‎ F E ‎∴AD∥BC，AD＝BC 又∵DE＝CF ‎∴AD－DE＝BC－CF，‎ 即AE＝BF ‎∵AE∥BF ‎∴四边形ABFE是平行四边形 又∵BE平分 ‎∴∠ABE＝∠EBF 又∵AD∥BC ‎∴∠AEB＝∠EBF ‎∴∠ABE＝∠AEB ‎∴AB＝AE ‎∴是菱形。‎ ‎24. 解：（1），‎ ‎ （2），‎ 图14‎ O A B D C E ‎25.解：（1）DE与相切，理由如下：‎ ‎ 连接AD、OD，‎ ‎ ∵为的直径 ‎∴∠BDA＝90°‎ ‎∴AD⊥BC 又∵AB＝AC ‎∴BD＝DC 又∵OB＝OA ‎∴OD是△ABC的中位线 ‎∴OD∥AC 又∵‎ ‎∴‎ ‎ ∴DE是的切线。‎ ‎（2）若的半径为，则AB＝AC＝5，‎ 在Rt△ADC中，AD＝3，AC＝5‎ ‎∴DC＝‎ 又∵AC·DE＝AD·DC ‎∴‎ ‎26.解：（1）本次问卷调查的样本容量是 200 ；‎ ‎（2）扇形统计图中，圆心角 72° ；‎ ‎（3）补全条形统计图（略）；‎ ‎（4）答案不唯一，建议合理即可．‎ ‎27.解：（1）由题可知：，即3x+3y=4x ‎ 所以y与x的函数关系式为.‎ ‎ （2）由（1）可知，当x=3时，y=1。袋中有3只白球和1只红球。‎ ‎ ‎ 白球1‎ 白球2‎ 白球3‎ 红球 白球1‎ ‎--------‎ ‎（白1，白2）‎ ‎（白1，白3）‎ ‎（白1，红）‎ 白球2‎ ‎（白2，白1）‎ ‎----------‎ ‎（白2，白3）‎ ‎（白2，红）‎ 白球3‎ ‎（白3，白1）‎ ‎（白3，白2）‎ ‎-----------‎ ‎（白3，红）‎ 红球 ‎（红，白1）‎ ‎（红，白2）‎ ‎（红，白3）‎ ‎-----------‎ 由上面列表可知：共有12种等可能的结果，其中两次都是白球的占6种，‎ 所以两次摸到都是白球的概率是.‎ ‎28.解：（1）如图17，∵的面积为‎24cm2 ，且OC=cm．‎ ‎ ∴=2×24÷6＝‎‎8cm ‎∴cm ‎∴BC＝cm.‎ ‎ （2）由（1）可知＝OA－＝10－8＝2‎ ‎ 设AM＝x，则BM＝＝6－x ‎ 由勾股定理可得方程：‎ ‎ 解得：‎ ‎ 所以M（10，），C（0，6）‎ 设所在直线的函数关系式为y＝kx+b 则 ，解得 ‎∴所在直线的函数关系式为.‎ ‎（3）∵，=8‎ ‎ ∴G点的横坐标为8，‎ 又∵点G在直线CM上，CM关系式为 所以G点的纵坐标为y＝‎ 即G（8，）.‎ ‎∵抛物线过点，‎ ‎∴‎ ‎∴‎ 所求抛物线的关系式为.‎ 注：以上答案为个人（郭新运）依题作答而成，并非原版答案录入。如发现答案有误，请不吝赐教指正，谢谢。gxy999@gmail.com。‎