2020年黑龙江省鹤岗市中考数学试卷(含解析） 30页

‎2020年黑龙江省鹤岗市中考数学试卷 一、选择题（每题3分，满分30分）‎ ‎1．（3分）下列各运算中，计算正确的是（　　）‎ A．a2•2a2＝2a4 B．x8÷x2＝x4 ‎ C．（x﹣y）2＝x2﹣xy+y2 D．（﹣3x2）3＝﹣9x6‎ ‎2．（3分）下列图标中是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎3．（3分）如图，由若干个相同的小正方体搭成的一个几何体的主视图和左视图，则所需的小正方体的个数最多是（　　）‎ A．6 B．7 C．8 D．9‎ ‎4．（3分）一组从小到大排列的数据：x，3，4，4，5（x为正整数），唯一的众数是4，则该组数据的平均数是（　　）‎ A．3.6 B．3.8或3.2 C．3.6或3.4 D．3.6或3.2‎ ‎5．（3分）已知关于x的一元二次方程x2﹣（2k+1）x+k2+2k＝0有两个实数根x1，x2，则实数k的取值范围是（　　）‎ A．k‎＜‎‎1‎‎4‎ B．k‎≤‎‎1‎‎4‎ C．k＞4 D．k‎≤‎‎1‎‎4‎且k≠0‎ ‎6．（3分）如图，菱形ABCD的两个顶点A，C在反比例函数y‎=‎kx的图象上，对角线AC，BD的交点恰好是坐标原点O，已知B（﹣1，1），∠ABC＝120°，则k的值是（　　）‎ A．5 B．4 C．3 D．2‎ ‎7．（3分）已知关于x的分式方程xx-2‎‎-‎4‎=‎k‎2-x的解为正数，则k的取值范围是（　　）‎ 第29页（共29页）‎ A．﹣8＜k＜0 B．k＞﹣8且k≠﹣2 C．k＞﹣8 且k≠2 D．k＜4且k≠﹣2‎ ‎8．（3分）如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，连接OH，若OA＝6，S菱形ABCD＝48，则OH的长为（　　）‎ A．4 B．8 C．‎13‎ D．6‎ ‎9．（3分）在抗击疫情网络知识竞赛中，为奖励成绩突出的学生，学校计划用200元钱购买A、B、C三种奖品，A种每个10元，B种每个20元，C种每个30元，在C种奖品不超过两个且钱全部用完的情况下，有多少种购买方案（　　）‎ A．12种 B．15种 C．16种 D．14种 ‎10．（3分）如图，正方形ABCD的边长为a，点E在边AB上运动（不与点A，B重合），∠DAM＝45°，点F在射线AM上，且AF‎=‎‎2‎BE，CF与AD相交于点G，连接EC、EF、EG．则下列结论：‎ ‎①∠ECF＝45°；‎ ‎②△AEG的周长为（1‎+‎‎2‎‎2‎）a；‎ ‎③BE2+DG2＝EG2；‎ ‎④△EAF的面积的最大值是‎1‎‎8‎a2；‎ ‎⑤当BE‎=‎‎1‎‎3‎a时，G是线段AD的中点．‎ 其中正确的结论是（　　）‎ A．①②③ B．②④⑤ C．①③④ D．①④⑤‎ 二、填空题（每题3分，满分30分）‎ 第29页（共29页）‎ ‎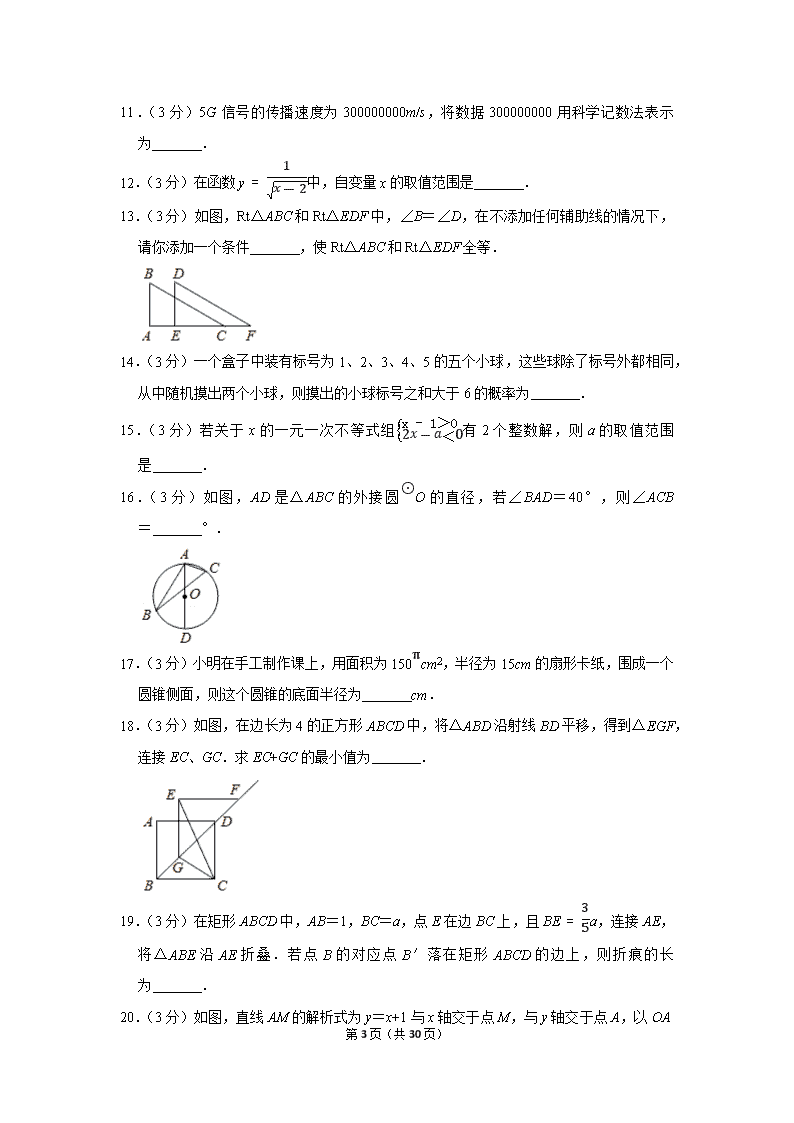11．（3分）5G信号的传播速度为300000000m/s，将数据300000000用科学记数法表示为　 　．‎ ‎12．（3分）在函数y‎=‎‎1‎x-2‎中，自变量x的取值范围是　 　．‎ ‎13．（3分）如图，Rt△ABC和Rt△EDF中，∠B＝∠D，在不添加任何辅助线的情况下，请你添加一个条件　 　，使Rt△ABC和Rt△EDF全等．‎ ‎14．（3分）一个盒子中装有标号为1、2、3、4、5的五个小球，这些球除了标号外都相同，从中随机摸出两个小球，则摸出的小球标号之和大于6的概率为　 　．‎ ‎15．（3分）若关于x的一元一次不等式组x-1＞0‎‎2x-a＜0‎有2个整数解，则a的取值范围是　 　．‎ ‎16．（3分）如图，AD是△ABC的外接圆⊙O的直径，若∠BAD＝40°，则∠ACB＝　 　°．‎ ‎17．（3分）小明在手工制作课上，用面积为150πcm2，半径为15cm的扇形卡纸，围成一个圆锥侧面，则这个圆锥的底面半径为　 　cm．‎ ‎18．（3分）如图，在边长为4的正方形ABCD中，将△ABD沿射线BD平移，得到△EGF，连接EC、GC．求EC+GC的最小值为　 　．‎ ‎19．（3分）在矩形ABCD中，AB＝1，BC＝a，点E在边BC上，且BE‎=‎‎3‎‎5‎a，连接AE，将△ABE沿AE折叠．若点B的对应点B′落在矩形ABCD的边上，则折痕的长为　 　．‎ ‎20．（3分）如图，直线AM的解析式为y＝x+1与x轴交于点M，与y轴交于点A，以OA 第29页（共29页）‎ 为边作正方形ABCO，点B坐标为（1，1）．过点B作EO1⊥MA交MA于点E，交x轴于点O1，过点O1作x轴的垂线交MA于点A1，以O1A1为边作正方形O1A1B1C1，点B1的坐标为（5，3）．过点B1作E1O2⊥MA交MA于E1，交x轴于点O2，过点O2作x轴的垂线交MA于点A2．以O2A2为边作正方形O2A2B2C2．…．则点B2020的坐标　 　．‎ 三、解答题（满分60分）‎ ‎21．（5分）先化简，再求值：（2‎-‎x-1‎x+1‎）‎÷‎x‎2‎‎+6x+9‎x‎2‎‎-1‎，其中x＝3tan30°﹣3．‎ ‎22．（6分）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点A（5，2）、B（5，5）、C（1，1）均在格点上．‎ ‎（1）将△ABC向左平移5个单位得到△A1B1C1，并写出点A1的坐标；‎ ‎（2）画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1，并写出点A2的坐标；‎ ‎（3）在（2）的条件下，求△A1B1C1在旋转过程中扫过的面积（结果保留π）．‎ ‎23．（6分）如图，已知二次函数y＝﹣x2+bx+c的图象经过点A（﹣1，0），B （3，0），与y轴交于点C．‎ ‎（1）求抛物线的解析式；‎ ‎（2）抛物线上是否存在点P，使∠PAB＝∠ABC，若存在请直接写出点P 第29页（共29页）‎ 的坐标．若不存在，请说明理由．‎ ‎24．（7分）为了提高学生体质，战胜疫情，某中学组织全校学生宅家一分钟跳绳比赛，全校跳绳平均成绩是每分钟99次，某班班长统计了全班50名学生一分钟跳绳成绩，列出的频数分布直方图如图所示，（每个小组包括左端点，不包括右端点）．‎ 求：（1）该班一分钟跳绳的平均次数至少是多少，是否超过全校的平均次数；‎ ‎（2）该班的一个学生说：“我的跳绳成绩是我班的中位数”请你给出该生跳绳成绩的所在范围；‎ ‎（3）从该班中任选一人，其跳绳次数超过全校平均数的概率是多少．‎ ‎25．（8分）为抗击疫情，支持武汉，某物流公司的快递车和货车每天往返于物流公司、武汉两地，快递车比货车多往返一趟，如图表示两车离物流公司的距离y（单位：千米）与快递车所用时间x（单位：时）的函数图象，已知货车比快递车早1小时出发，到达武汉后用2小时装卸货物，按原速、原路返回，货车比快递车最后一次返回物流公司晚1小时．‎ 第29页（共29页）‎ ‎（1）求ME的函数解析式；‎ ‎（2）求快递车第二次往返过程中，与货车相遇的时间．‎ ‎（3）求两车最后一次相遇时离武汉的距离．（直接写出答案）‎ ‎26．（8分）如图①，在Rt△ABC中，∠ACB＝90°，AC＝BC，点D、E分别在AC、BC边上，DC＝EC，连接DE、AE、BD，点M、N、P分别是AE、BD、AB的中点，连接PM、PN、MN．‎ ‎（1）BE与MN的数量关系是　 　．‎ ‎（2）将△DEC绕点C逆时针旋转到图②和图③的位置，判断BE与MN有怎样的数量关系？写出你的猜想，并利用图②或图③进行证明．‎ ‎27．（10分）某农谷生态园响应国家发展有机农业政策，大力种植有机蔬菜，某超市看好甲、乙两种有机蔬菜的市场价值，经调查甲种蔬菜进价每千克m元，售价每千克16元；乙种蔬菜进价每千克n元，售价每千克18元．‎ ‎（1）该超市购进甲种蔬菜15千克和乙种蔬菜20千克需要430元；购进甲种蔬菜10千克和乙种蔬菜8千克需要212元，求m，n的值．‎ ‎（2）该超市决定每天购进甲、乙两种蔬菜共100千克，且投入资金不少于1160元又不多于1168元，设购买甲种蔬菜x千克（x为正整数），求有哪几种购买方案．‎ 第29页（共29页）‎ ‎（3）在（2）的条件下，超市在获得的利润取得最大值时，决定售出的甲种蔬菜每千克捐出2a元，乙种蔬菜每千克捐出a元给当地福利院，若要保证捐款后的利润率不低于20%，求a的最大值．‎ ‎28．（10分）如图，在平面直角坐标系中，矩形ABCD的边AB长是x2﹣3x﹣18＝0的根，连接BD，∠DBC＝30°，并过点C作CN⊥BD，垂足为N，动点P从B点以每秒2个单位长度的速度沿BD方向匀速运动到D点为止；点M沿线段DA以每秒‎3‎个单位长度的速度由点D向点A匀速运动，到点A为止，点P与点M同时出发，设运动时间为t秒（t＞0）．‎ ‎（1）线段CN＝　 　；‎ ‎（2）连接PM和MN，求△PMN的面积s与运动时间t的函数关系式；‎ ‎（3）在整个运动过程中，当△PMN是以PN为腰的等腰三角形时，直接写出点P的坐标．‎ 第29页（共29页）‎ ‎2020年黑龙江省鹤岗市中考数学试卷 参考答案与试题解析 一、选择题（每题3分，满分30分）‎ ‎1．（3分）下列各运算中，计算正确的是（　　）‎ A．a2•2a2＝2a4 B．x8÷x2＝x4 ‎ C．（x﹣y）2＝x2﹣xy+y2 D．（﹣3x2）3＝﹣9x6‎ ‎【解答】解：A、a2•2a2＝2a4，正确；‎ B、x8÷x2＝x6，故此选项错误；‎ C、（x﹣y）2＝x2﹣2xy+y2，故此选项错误；‎ D、（﹣3x2）3＝﹣27x6，故此选项错误；‎ 故选：A．‎ ‎2．（3分）下列图标中是中心对称图形的是（　　）‎ A． B． C． D．‎ ‎【解答】解：A．是轴对称图形，不是中心对称图形，故本选项不合题意；‎ B．是中心对称图形，故本选项符合题意；‎ C．是轴对称图形，不是中心对称图形，故本选项不合题意；‎ D．是轴对称图形，不是中心对称图形，故本选项不合题意．‎ 故选：B．‎ ‎3．（3分）如图，由若干个相同的小正方体搭成的一个几何体的主视图和左视图，则所需的小正方体的个数最多是（　　）‎ A．6 B．7 C．8 D．9‎ ‎【解答】解：综合主视图与左视图，第一行第1列最多有2个，第一行第2列最多有1个；‎ 第二行第1列最多有3个，第二行第2列最多有1个；‎ 所以最多有：2+1+3+1＝7（个）．‎ 第29页（共29页）‎ 故选：B．‎ ‎4．（3分）一组从小到大排列的数据：x，3，4，4，5（x为正整数），唯一的众数是4，则该组数据的平均数是（　　）‎ A．3.6 B．3.8或3.2 C．3.6或3.4 D．3.6或3.2‎ ‎【解答】解：∵从小到大排列的数据：x，3，4，4，5（x为正整数），唯一的众数是4，‎ ‎∴x＝2或x＝1，‎ 当x＝2时，这组数据的平均数为‎2+3+4+4+5‎‎5‎‎=‎3.6；‎ 当x＝1时，这组数据的平均数为‎1+3+4+4+5‎‎5‎‎=‎3.4；‎ 即这组数据的平均数为3.4或3.6，‎ 故选：C．‎ ‎5．（3分）已知关于x的一元二次方程x2﹣（2k+1）x+k2+2k＝0有两个实数根x1，x2，则实数k的取值范围是（　　）‎ A．k‎＜‎‎1‎‎4‎ B．k‎≤‎‎1‎‎4‎ C．k＞4 D．k‎≤‎‎1‎‎4‎且k≠0‎ ‎【解答】解：∵关于x的一元二次方程x2﹣（2k+1）x+k2+2k＝0有两个实数根x1，x2，‎ ‎∴△＝[﹣（2k+1）]2﹣4×1×（k2+2k）≥0，‎ 解得：k‎≤‎‎1‎‎4‎．‎ 故选：B．‎ ‎6．（3分）如图，菱形ABCD的两个顶点A，C在反比例函数y‎=‎kx的图象上，对角线AC，BD的交点恰好是坐标原点O，已知B（﹣1，1），∠ABC＝120°，则k的值是（　　）‎ A．5 B．4 C．3 D．2‎ ‎【解答】解：∵四边形ABCD是菱形，‎ ‎∴BA＝AD，AC⊥BD，‎ ‎∵∠ABC＝120°，‎ ‎∴∠BAD＝60°，‎ 第29页（共29页）‎ ‎∴△ABD是等边三角形，‎ ‎∵点B（﹣1，1），‎ ‎∴OB‎=‎‎2‎，‎ ‎∴AO‎=OBtan30°‎=‎‎6‎，‎ ‎∵直线BD的解析式为y＝﹣x，‎ ‎∴直线AD的解析式为y＝x，‎ ‎∵OA‎=‎‎6‎，‎ ‎∴点A的坐标为（‎3‎，‎3‎），‎ ‎∵点A在反比例函数y‎=‎kx的图象上，‎ ‎∴k‎=‎3‎×‎3‎=‎3，‎ 故选：C．‎ ‎7．（3分）已知关于x的分式方程xx-2‎‎-‎4‎=‎k‎2-x的解为正数，则k的取值范围是（　　）‎ A．﹣8＜k＜0 B．k＞﹣8且k≠﹣2 C．k＞﹣8 且k≠2 D．k＜4且k≠﹣2‎ ‎【解答】解：分式方程xx-2‎‎-‎4‎=‎k‎2-x，‎ 去分母得：x﹣4（x﹣2）＝﹣k，‎ 去括号得：x﹣4x+8＝﹣k，‎ 解得：x‎=‎k+8‎‎3‎，‎ 由分式方程的解为正数，得到k+8‎‎3‎‎＞‎0，且k+8‎‎3‎‎≠‎2，‎ 解得：k＞﹣8且k≠﹣2．‎ 故选：B．‎ ‎8．（3分）如图，菱形ABCD的对角线AC、BD相交于点O，过点D作DH⊥AB于点H，连接OH，若OA＝6，S菱形ABCD＝48，则OH的长为（　　）‎ A．4 B．8 C．‎13‎ D．6‎ 第29页（共29页）‎ ‎【解答】解：∵四边形ABCD是菱形，‎ ‎∴OA＝OC＝6，OB＝OD，AC⊥BD，‎ ‎∴AC＝12，‎ ‎∵DH⊥AB，‎ ‎∴∠BHD＝90°，‎ ‎∴OH‎=‎‎1‎‎2‎BD，‎ ‎∵菱形ABCD的面积‎=‎1‎‎2‎×‎AC×BD‎=‎1‎‎2‎×‎12×BD＝48，‎ ‎∴BD＝8，‎ ‎∴OH‎=‎‎1‎‎2‎BD＝4；‎ 故选：A．‎ ‎9．（3分）在抗击疫情网络知识竞赛中，为奖励成绩突出的学生，学校计划用200元钱购买A、B、C三种奖品，A种每个10元，B种每个20元，C种每个30元，在C种奖品不超过两个且钱全部用完的情况下，有多少种购买方案（　　）‎ A．12种 B．15种 C．16种 D．14种 ‎【解答】解：设购买A种奖品m个，购买B种奖品n个，‎ 当C种奖品个数为1个时，‎ 根据题意得10m+20n+30＝200，‎ 整理得m+2n＝17，‎ ‎∵m、n都是正整数，0＜2m＜17，‎ ‎∴m＝1，2，3，4，5，6，7，8；‎ 当C种奖品个数为2个时，‎ 根据题意得10m+20n+60＝200，‎ 整理得m+2n＝14，‎ ‎∵m、n都是正整数，0＜2m＜14，‎ ‎∴m＝1，2，3，4，5，6；‎ ‎∴有8+6＝14种购买方案．‎ 故选：D．‎ ‎10．（3分）如图，正方形ABCD的边长为a，点E在边AB上运动（不与点A，B重合），∠DAM＝45°，点F在射线AM上，且AF‎=‎‎2‎BE，CF与AD相交于点G，连接EC、‎ 第29页（共29页）‎ EF、EG．则下列结论：‎ ‎①∠ECF＝45°；‎ ‎②△AEG的周长为（1‎+‎‎2‎‎2‎）a；‎ ‎③BE2+DG2＝EG2；‎ ‎④△EAF的面积的最大值是‎1‎‎8‎a2；‎ ‎⑤当BE‎=‎‎1‎‎3‎a时，G是线段AD的中点．‎ 其中正确的结论是（　　）‎ A．①②③ B．②④⑤ C．①③④ D．①④⑤‎ ‎【解答】解：如图1中，在BC上截取BH＝BE，连接EH．‎ ‎∵BE＝BH，∠EBH＝90°，‎ ‎∴EH‎=‎‎2‎BE，‎ ‎∵AF‎=‎‎2‎BE，‎ ‎∴AF＝EH，‎ ‎∵∠DAM＝∠EHB＝45°，∠BAD＝90°，‎ ‎∴∠FAE＝∠EHC＝135°，‎ ‎∵BA＝BC，BE＝BH，‎ ‎∴AE＝HC，‎ ‎∴△FAE≌△EHC（SAS），‎ ‎∴EF＝EC，∠AEF＝∠ECH，‎ ‎∵∠ECH+∠CEB＝90°，‎ ‎∴∠AEF+∠CEB＝90°，‎ ‎∴∠FEC＝90°，‎ ‎∴∠ECF＝∠EFC＝45°，故①正确，‎ 第29页（共29页）‎ 如图2中，延长AD到H，使得DH＝BE，则△CBE≌△CDH（SAS），‎ ‎∴∠ECB＝∠DCH，‎ ‎∴∠ECH＝∠BCD＝90°，‎ ‎∴∠ECG＝∠GCH＝45°，‎ ‎∵CG＝CG，CE＝CH，‎ ‎∴△GCE≌△GCH（SAS），‎ ‎∴EG＝GH，‎ ‎∵GH＝DG+DH，DH＝BE，‎ ‎∴EG＝BE+DG，故③错误，‎ ‎∴△AEG的周长＝AE+EG+AG＝AE+AH＝AD+DH+AE＝AE+EB+AD＝AB+AD＝2a，故②错误，‎ 设BE＝x，则AE＝a﹣x，AF‎=‎‎2‎x，‎ ‎∴S△AEF‎=‎‎1‎‎2‎•（a﹣x）×x‎=-‎‎1‎‎2‎x2‎+‎‎1‎‎2‎ax‎=-‎‎1‎‎2‎（x2﹣ax‎+‎‎1‎‎4‎a2‎-‎‎1‎‎4‎a2）‎=-‎‎1‎‎2‎（x‎-‎‎1‎‎2‎a）2‎+‎‎1‎‎8‎a2，‎ ‎∵‎-‎1‎‎2‎＜‎0，‎ ‎∴x‎=‎‎1‎‎2‎a时，△AEF的面积的最大值为‎1‎‎8‎a2．故④正确，‎ 当BE‎=‎‎1‎‎3‎a时，设DG＝x，则EG＝x‎+‎‎1‎‎3‎a，‎ 在Rt△AEG中，则有（x‎+‎‎1‎‎3‎a）2＝（a﹣x）2+（‎2‎‎3‎a）2，‎ 解得x‎=‎a‎2‎，‎ ‎∴AG＝GD，故⑤正确，‎ 故选：D．‎ 第29页（共29页）‎ 二、填空题（每题3分，满分30分）‎ ‎11．（3分）5G信号的传播速度为300000000m/s，将数据300000000用科学记数法表示为　3×108　．‎ ‎【解答】解：300000000＝3×108．‎ 故答案为：3×108．‎ ‎12．（3分）在函数y‎=‎‎1‎x-2‎中，自变量x的取值范围是　x＞2　．‎ ‎【解答】解：由题意得，x﹣2＞0，‎ 解得x＞2．‎ 故答案为：x＞2．‎ ‎13．（3分）如图，Rt△ABC和Rt△EDF中，∠B＝∠D，在不添加任何辅助线的情况下，请你添加一个条件　AB＝ED（BC＝DF或AC＝EF或AE＝CF等）　，使Rt△ABC和Rt△EDF全等．‎ ‎【解答】解：添加的条件是：AB＝ED，‎ 理由是：∵在△ABC和△EDF中 ‎∠B=∠DAB=ED‎∠A=∠DEF‎，‎ ‎∴△ABC≌△EDF（ASA），‎ 故答案为：AB＝ED．‎ ‎14．（3分）一个盒子中装有标号为1、2、3、4、5的五个小球，这些球除了标号外都相同，从中随机摸出两个小球，则摸出的小球标号之和大于6的概率为　‎2‎‎5‎　．‎ 第29页（共29页）‎ ‎【解答】解：画树状图如图所示：‎ ‎∵共有20种等可能的结果，摸出的两个小球的标号之和大于6的有8种结果，‎ ‎∴摸出的两个小球的标号之和大于6的概率为‎8‎‎20‎‎=‎‎2‎‎5‎，‎ 故答案为：‎2‎‎5‎．‎ ‎15．（3分）若关于x的一元一次不等式组x-1＞0‎‎2x-a＜0‎有2个整数解，则a的取值范围是　6＜a≤8　．‎ ‎【解答】解：解不等式x﹣1＞0，得：x＞1，‎ 解不等式2x﹣a＜0，得：x‎＜‎a‎2‎，‎ 则不等式组的解集为1＜x‎＜‎a‎2‎，‎ ‎∵不等式组有2个整数解，‎ ‎∴不等式组的整数解为2、3，‎ 则3‎＜a‎2‎≤‎4，‎ 解得6＜a≤8，‎ 故答案为：6＜a≤8．‎ ‎16．（3分）如图，AD是△ABC的外接圆⊙O的直径，若∠BAD＝40°，则∠ACB＝　50　°．‎ ‎【解答】解：连接BD，如图，‎ ‎∵AD为△ABC的外接圆⊙O的直径，‎ ‎∴∠ABD＝90°，‎ ‎∴∠D＝90°﹣∠BAD＝90°﹣40°＝50°，‎ 第29页（共29页）‎ ‎∴∠ACB＝∠D＝50°．‎ 故答案为50．‎ ‎17．（3分）小明在手工制作课上，用面积为150πcm2，半径为15cm的扇形卡纸，围成一个圆锥侧面，则这个圆锥的底面半径为　10　cm．‎ ‎【解答】解：∵S‎=‎‎1‎‎2‎l•R，‎ ‎∴‎1‎‎2‎•l•15＝150π，解得l＝20π，‎ 设圆锥的底面半径为r，‎ ‎∴2π•r＝20π，‎ ‎∴r＝10（cm）．‎ 故答案为：10．‎ ‎18．（3分）如图，在边长为4的正方形ABCD中，将△ABD沿射线BD平移，得到△EGF，连接EC、GC．求EC+GC的最小值为　4‎5‎　．‎ ‎【解答】解：如图，连接DE，作点D关于直线AE的对称点T，连接AT，ET，CT．‎ ‎∵四边形ABCD是正方形，‎ ‎∴AB＝BC═AD＝4，∠ABC＝90°，∠ABD＝45°，‎ ‎∵AE∥BD，‎ 第29页（共29页）‎ ‎∴∠EAD＝∠ABD＝45°，‎ ‎∵D，T关于AE对称，‎ ‎∴AD＝AT＝4，∠TAE＝∠EAD＝45°，‎ ‎∴∠TAD＝90°，‎ ‎∵∠BAD＝90°，‎ ‎∴B，A，T共线，‎ ‎∴CT‎=BT‎2‎+BC‎2‎=‎4‎5‎，‎ ‎∵EG＝CD，EG∥CD，‎ ‎∴四边形EGCD是平行四边形，‎ ‎∴CG＝EC，‎ ‎∴EC+CG＝EC+ED＝EC+TE，‎ ‎∵TE+EC≥TC，‎ ‎∴EC+CG≥4‎5‎，‎ ‎∴EC+CG的最小值为4‎5‎．‎ ‎19．（3分）在矩形ABCD中，AB＝1，BC＝a，点E在边BC上，且BE‎=‎‎3‎‎5‎a，连接AE，将△ABE沿AE折叠．若点B的对应点B′落在矩形ABCD的边上，则折痕的长为　‎2‎或‎30‎‎5‎　．‎ ‎【解答】解：分两种情况：‎ ‎①当点B'落在AD边上时，如图1所示：‎ ‎∵四边形ABCD是矩形，‎ ‎∴∠BAD＝∠B＝90°，‎ ‎∵将△ABE沿AE折叠．点B的对应点B′落在矩形ABCD的AD边上，‎ ‎∴∠BAE＝∠B'AE‎=‎‎1‎‎2‎∠BAD＝45°，‎ ‎∴△ABE是等腰直角三角形，‎ ‎∴AB＝BE＝1，AE‎=‎‎2‎AB‎=‎‎2‎；‎ 第29页（共29页）‎ ‎②当点B'落在CD边上时，如图2所示：‎ ‎∵四边形ABCD是矩形，‎ ‎∴∠BAD＝∠B＝∠C＝∠D＝90°，AD＝BC＝a，‎ ‎∵将△ABE沿AE折叠．点B的对应点B′落在矩形ABCD的CD边上，‎ ‎∴∠B＝∠AB'E＝90°，AB'＝AB＝1，BE'＝BE‎=‎‎3‎‎5‎a，‎ ‎∴CE＝BC﹣BE＝a‎-‎‎3‎‎5‎a‎=‎‎2‎‎5‎a，B'D‎=AB‎'‎‎2‎-AD‎2‎=‎‎1-‎a‎2‎，‎ 在△ADB'和△B'CE中，∠B'AD＝∠EB'C＝90°﹣∠AB'D，∠D＝∠C＝90°，‎ ‎∴△ADB'∽△B'CE，‎ ‎∴B'DEC‎=‎AB'‎B'E，即‎1-‎a‎2‎‎2‎‎5‎a‎=‎‎1‎‎3‎‎5‎a，‎ 解得：a‎=‎‎5‎‎3‎，或a＝0（舍去），‎ ‎∴BE‎=‎‎3‎‎5‎a‎=‎‎5‎‎5‎，‎ ‎∴AE‎=AB‎2‎+BE‎2‎=‎1‎‎2‎‎+(‎‎5‎‎5‎‎)‎‎2‎=‎‎30‎‎5‎；‎ 综上所述，折痕的长为‎2‎或‎30‎‎5‎；‎ 故答案为：‎2‎或‎30‎‎5‎．‎ ‎20．（3分）如图，直线AM的解析式为y＝x+1与x轴交于点M，与y轴交于点A，以OA为边作正方形ABCO，点B坐标为（1，1）．过点B作EO1⊥MA交MA于点E，交x轴于点O1，过点O1作x轴的垂线交MA于点A1，以O1A1为边作正方形O1A1B1C1，点B1的坐标为（5，3）．过点B1作E1O2⊥MA交MA于E1，交x轴于点O2，过点O2作x轴的垂线交MA于点A2．以O2A2为边作正方形O2A2B2C2．…．则点B2020的坐标　2×32020﹣1，32020　．‎ 第29页（共29页）‎ ‎【解答】解：∵点B坐标为（1，1），‎ ‎∴OA＝AB＝BC＝CO＝CO1＝1，‎ ‎∵A1（2，3），‎ ‎∴A1O1＝A1B1＝B1C1＝C1O2＝3，‎ ‎∴B1（5，3），‎ ‎∴A2（8，9），‎ ‎∴A2O2＝A2B2＝B2C2＝C2O3＝9，‎ ‎∴B2（17，9），‎ 同理可得B4（53，27），‎ B5（161，81），‎ ‎…‎ 由上可知，Bn（2×3n﹣1，3n），‎ ‎∴当n＝2020时，Bn（2×32020﹣1，32020）．‎ 故答案为：（2×32020﹣1，32020）．‎ 三、解答题（满分60分）‎ ‎21．（5分）先化简，再求值：（2‎-‎x-1‎x+1‎）‎÷‎x‎2‎‎+6x+9‎x‎2‎‎-1‎，其中x＝3tan30°﹣3．‎ ‎【解答】解：原式＝（‎2x+2‎x+1‎‎-‎x-1‎x+1‎）‎‎÷‎‎(x+3‎‎)‎‎2‎‎(x+1)(x-1)‎ ‎=‎x+3‎x+1‎‎•‎(x+1)(x-1)‎‎(x+3‎‎)‎‎2‎ ‎ ‎=‎x-1‎x+3‎‎，‎ 当x＝3tan30°﹣3＝3‎×‎3‎‎3‎-‎3‎=‎3‎-‎3时，‎ 原式‎=‎‎3‎‎-3-1‎‎3‎‎-3+3‎ 第29页（共29页）‎ ‎=‎‎3‎‎-4‎‎3‎‎ ‎ ‎＝1‎-‎‎4‎‎3‎‎3‎．‎ ‎22．（6分）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△ABC的三个顶点A（5，2）、B（5，5）、C（1，1）均在格点上．‎ ‎（1）将△ABC向左平移5个单位得到△A1B1C1，并写出点A1的坐标；‎ ‎（2）画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1，并写出点A2的坐标；‎ ‎（3）在（2）的条件下，求△A1B1C1在旋转过程中扫过的面积（结果保留π）．‎ ‎【解答】解：（1）如图所示，△A1B1C1即为所求，点A1的坐标为（0，2）；‎ ‎（2）如图所示，△A2B2C1即为所求，点A2的坐标为（﹣3，﹣3）；‎ ‎（3）如图，‎ ‎∵BC‎=‎4‎‎2‎‎+‎‎4‎‎2‎=‎4‎2‎，‎ ‎∴△A1B1C1在旋转过程中扫过的面积为：‎90π×(4‎‎2‎‎)‎‎2‎‎360‎‎+‎1‎‎2‎×‎3×4＝8π+6．‎ 第29页（共29页）‎ ‎23．（6分）如图，已知二次函数y＝﹣x2+bx+c的图象经过点A（﹣1，0），B （3，0），与y轴交于点C．‎ ‎（1）求抛物线的解析式；‎ ‎（2）抛物线上是否存在点P，使∠PAB＝∠ABC，若存在请直接写出点P的坐标．若不存在，请说明理由．‎ ‎【解答】解：（1）根据题意得‎-1-b+c=0‎‎-9+3b+c=0‎，‎ 解得b=2‎c=3‎．‎ 故抛物线的解析式为y＝﹣x2+2x+3；‎ ‎（2）二次函数y＝﹣x2+2x+3的对称轴是x＝（﹣1+3）÷2＝1，‎ 当x＝0时，y＝3，‎ 则C（0，3），‎ 点C关于对称轴的对应点P1（2，3），‎ 设直线BC的解析式为y＝kx+3，‎ 则3k+3＝0，‎ 解得k＝﹣1．‎ 则直线BC的解析式为y＝﹣x+3，‎ 设与BC平行的直线AP的解析式为y＝﹣x+m，‎ 则1+m＝0，‎ 解得m＝﹣1．‎ 则与BC平行的直线AP的解析式为y＝﹣x﹣1，‎ 联立抛物线解析式得y=-x-1‎y=-x‎2‎+2x+3‎，‎ 解得x‎1‎‎=4‎y‎1‎‎=-5‎，x‎2‎‎=-1‎y‎2‎‎=0‎（舍去）．‎ P2（4，﹣5）．‎ 第29页（共29页）‎ 综上所述，P1（2，3），P2（4，﹣5）．‎ ‎24．（7分）为了提高学生体质，战胜疫情，某中学组织全校学生宅家一分钟跳绳比赛，全校跳绳平均成绩是每分钟99次，某班班长统计了全班50名学生一分钟跳绳成绩，列出的频数分布直方图如图所示，（每个小组包括左端点，不包括右端点）．‎ 求：（1）该班一分钟跳绳的平均次数至少是多少，是否超过全校的平均次数；‎ ‎（2）该班的一个学生说：“我的跳绳成绩是我班的中位数”请你给出该生跳绳成绩的所在范围；‎ ‎（3）从该班中任选一人，其跳绳次数超过全校平均数的概率是多少．‎ ‎【解答】解：（1）该班一分钟跳绳的平均次数至少是：‎60×4+80×13+100×19+120×7+140×5+160×2‎‎50‎‎=‎100.8，‎ ‎∵100.8＞100，‎ ‎∴超过全校的平均次数；‎ ‎（2）这个学生的跳绳成绩在该班是中位数，因为4+13+19＝36，所以中位数一定在100～120范围内；‎ ‎（3）该班60秒跳绳成绩大于或等于100次的有：19+7+5+2＝33（人），‎ 第29页（共29页）‎ 故从该班中任选一人，其跳绳次数超过全校平均数的概率是‎33‎‎50‎．‎ ‎25．（8分）为抗击疫情，支持武汉，某物流公司的快递车和货车每天往返于物流公司、武汉两地，快递车比货车多往返一趟，如图表示两车离物流公司的距离y（单位：千米）与快递车所用时间x（单位：时）的函数图象，已知货车比快递车早1小时出发，到达武汉后用2小时装卸货物，按原速、原路返回，货车比快递车最后一次返回物流公司晚1小时．‎ ‎（1）求ME的函数解析式；‎ ‎（2）求快递车第二次往返过程中，与货车相遇的时间．‎ ‎（3）求两车最后一次相遇时离武汉的距离．（直接写出答案）‎ ‎【解答】解：（1）设ME的函数解析式为y＝kx+b（k≠0），由ME经过（0，50），（3，200）可得：‎ b=50‎‎3k+b=200‎‎，解得k=50‎b=50‎，‎ ‎∴ME的解析式为y＝50x+50；‎ ‎（2）设BC的函数解析式为y＝mx+n，由BC经过（4，0），（6，200）可得：‎ ‎4m+n=0‎‎6m+n=200‎‎，解得m=100‎n=-400‎，‎ ‎∴BC的函数解析式为y＝100x﹣400；‎ 设FG的函数解析式为y＝px+q，由FG经过（5，200），（9，0）可得：‎ ‎5p+q=200‎‎9p+q=0‎‎，解得p=-50‎q=450‎，‎ ‎∴FG的函数解析式为y＝﹣50x+450，‎ 第29页（共29页）‎ 解方程组y=100x-400‎y=-50x+450‎得x=‎‎17‎‎3‎y=‎‎500‎‎3‎，‎ 同理可得x＝7h，‎ 答：货车返回时与快递车图中相遇的时间‎17‎‎3‎h，7h；‎ ‎（3）（9﹣7）×50＝100（km），‎ 答：两车最后一次相遇时离武汉的距离为100km．‎ ‎26．（8分）如图①，在Rt△ABC中，∠ACB＝90°，AC＝BC，点D、E分别在AC、BC边上，DC＝EC，连接DE、AE、BD，点M、N、P分别是AE、BD、AB的中点，连接PM、PN、MN．‎ ‎（1）BE与MN的数量关系是　BE‎=‎‎2‎NM　．‎ ‎（2）将△DEC绕点C逆时针旋转到图②和图③的位置，判断BE与MN有怎样的数量关系？写出你的猜想，并利用图②或图③进行证明．‎ ‎【解答】解：（1）如图①中，‎ ‎∵AM＝ME，AP＝PB，‎ ‎∴PM∥BE，PM‎=‎‎1‎‎2‎BE，‎ 第29页（共29页）‎ ‎∵BN＝DN，AP＝PB，‎ ‎∴PN∥AD，PN‎=‎‎1‎‎2‎AD，‎ ‎∵AC＝BC，CD＝CE，‎ ‎∴AD＝BE，‎ ‎∴PM＝PN，‎ ‎∵∠ACB＝90°，‎ ‎∴AC⊥BC，‎ ‎∴∵PM∥BC，PN∥AC，‎ ‎∴PM⊥PN，‎ ‎∴△PMN的等腰直角三角形，‎ ‎∴MN‎=‎‎2‎PM，‎ ‎∴MN‎=‎‎2‎•‎1‎‎2‎BE，‎ ‎∴BE‎=‎‎2‎MN，‎ 故答案为BE‎=‎‎2‎MN．‎ ‎（2）如图②中，结论仍然成立．‎ 理由：连接AD，延长BE交AD于点H．‎ ‎∵△ABC和△CDE是等腰直角三角形，‎ ‎∴CD＝CE，CA＝CB，∠ACB＝∠DCE＝90°，‎ ‎∵∠ACB﹣∠ACE＝∠DCE﹣∠ACE，‎ ‎∴∠ACD＝∠ECB，‎ ‎∴△ECB≌△DCA（AAS），‎ ‎∴BE＝AD，∠DAC＝∠EBC，‎ ‎∵∠AHB＝180°﹣（∠HAB+∠ABH）‎ 第29页（共29页）‎ ‎＝180°﹣（45°+∠HAC+∠ABH）‎ ‎＝∠180°﹣（45°+∠HBC+∠ABH）‎ ‎＝180°﹣90°‎ ‎＝90°，‎ ‎∴BH⊥AD，‎ ‎∵M、N、P分别为AE、BD、AB的中点，‎ ‎∴PM∥BE，PM‎=‎‎1‎‎2‎BE，PN∥AD，PN‎=‎‎1‎‎2‎AD，‎ ‎∴PM＝PN，∠MPN＝90°，‎ ‎∴BE＝2PM＝2‎×‎‎2‎‎2‎MN‎=‎‎2‎MN．‎ ‎27．（10分）某农谷生态园响应国家发展有机农业政策，大力种植有机蔬菜，某超市看好甲、乙两种有机蔬菜的市场价值，经调查甲种蔬菜进价每千克m元，售价每千克16元；乙种蔬菜进价每千克n元，售价每千克18元．‎ ‎（1）该超市购进甲种蔬菜15千克和乙种蔬菜20千克需要430元；购进甲种蔬菜10千克和乙种蔬菜8千克需要212元，求m，n的值．‎ ‎（2）该超市决定每天购进甲、乙两种蔬菜共100千克，且投入资金不少于1160元又不多于1168元，设购买甲种蔬菜x千克（x为正整数），求有哪几种购买方案．‎ ‎（3）在（2）的条件下，超市在获得的利润取得最大值时，决定售出的甲种蔬菜每千克捐出2a元，乙种蔬菜每千克捐出a元给当地福利院，若要保证捐款后的利润率不低于20%，求a的最大值．‎ ‎【解答】解：（1）依题意，得：‎15m+20n=430‎‎10m+8n=212‎，‎ 解得：m=10‎n=14‎．‎ 答：m的值为10，n的值为14．‎ ‎（2）依题意，得：‎10x+14(100-x)≥1160‎‎10x+14(100-x)≤1168‎，‎ 解得：58≤x≤60．‎ 又∵x为正整数，‎ ‎∴x可以为58，59，60，‎ ‎∴共有3种购买方案，方案1：购进58千克甲种蔬菜，42千克乙种蔬菜；方案2：购进59千克甲种蔬菜，41千克乙种蔬菜；方案3：购进60千克甲种蔬菜，40千克乙种蔬菜．‎ 第29页（共29页）‎ ‎（3）购买方案1的总利润为（16﹣10）×58+（18﹣14）×42＝516（元）；‎ 购买方案2的总利润为（16﹣10）×59+（18﹣14）×41＝518（元）；‎ 购买方案3的总利润为（16﹣10）×60+（18﹣14）×40＝520（元）．‎ ‎∵516＜518＜520，‎ ‎∴利润最大值为520元，即售出甲种蔬菜60千克，乙种蔬菜40千克．‎ 依题意，得：（16﹣10﹣2a）×60+（18﹣14﹣a）×40≥（10×60+14×40）×20%，‎ 解得：a‎≤‎‎9‎‎5‎．‎ 答：a的最大值为‎9‎‎5‎．‎ ‎28．（10分）如图，在平面直角坐标系中，矩形ABCD的边AB长是x2﹣3x﹣18＝0的根，连接BD，∠DBC＝30°，并过点C作CN⊥BD，垂足为N，动点P从B点以每秒2个单位长度的速度沿BD方向匀速运动到D点为止；点M沿线段DA以每秒‎3‎个单位长度的速度由点D向点A匀速运动，到点A为止，点P与点M同时出发，设运动时间为t秒（t＞0）．‎ ‎（1）线段CN＝　3‎3‎　；‎ ‎（2）连接PM和MN，求△PMN的面积s与运动时间t的函数关系式；‎ ‎（3）在整个运动过程中，当△PMN是以PN为腰的等腰三角形时，直接写出点P的坐标．‎ ‎【解答】解：（1）∵AB长是x2﹣3x﹣18＝0的根，‎ ‎∴AB＝6，‎ ‎∵四边形ABCD是矩形，‎ ‎∴AD＝BC，AB＝CD＝6，∠BCD＝90°，‎ ‎∵∠DBC＝30°，‎ ‎∴BD＝2CD＝12，BC‎=‎‎3‎CD＝6‎3‎，‎ 第29页（共29页）‎ ‎∵∠DBC＝30°，CN⊥BD，‎ ‎∴CN‎=‎‎1‎‎2‎BC＝3‎3‎，‎ 故答案为：3‎3‎．‎ ‎（2）如图，过点M作MH⊥BD于H，‎ ‎∵AD∥BC，‎ ‎∴∠ADB＝∠DBC＝30°，‎ ‎∴MH‎=‎‎1‎‎2‎MD‎=‎‎3‎‎2‎t，‎ ‎∵∠DBC＝30°，CN⊥BD，‎ ‎∴BN‎=‎‎3‎CN＝9，‎ 当0＜t‎＜‎‎9‎‎2‎时，△PMN的面积s‎=‎1‎‎2‎×‎（9﹣2t）‎×‎‎3‎‎2‎t‎=-‎‎3‎‎2‎t2‎+‎‎9‎‎3‎‎4‎t；‎ 当t‎=‎‎9‎‎2‎时，点P与点N重合，s＝0，‎ 当‎9‎‎2‎‎＜‎t≤6时，△PMN的面积s‎=‎1‎‎2‎×‎（2t﹣9）‎×‎‎3‎‎2‎t‎=‎‎3‎‎2‎t2‎-‎‎9‎‎3‎‎4‎t；‎ ‎（3）如图，过点P作PE⊥BC于E，‎ 当PN＝PM＝9﹣2t时，‎ ‎∵PM2＝MH2+PH2，‎ 第29页（共29页）‎ ‎∴（9﹣2t）2＝（‎3‎‎2‎t）2+（12﹣2t‎-‎‎3‎‎2‎t）2，‎ ‎∴t＝3或t‎=‎‎7‎‎3‎，‎ ‎∴BP＝6或‎14‎‎3‎，‎ 当BP＝6时，‎ ‎∵∠DBC＝30°，PE⊥BC，‎ ‎∴PE‎=‎‎1‎‎2‎BP＝3，BE‎=‎‎3‎PE＝3‎3‎，‎ ‎∴点P（3‎3‎，3），‎ 当BP‎=‎‎14‎‎3‎时，‎ 同理可求点P（‎7‎‎3‎‎3‎，‎7‎‎3‎），‎ 当PN＝NM＝9﹣2t时，‎ ‎∵NM2＝MH2+NH2，‎ ‎∴（9﹣2t）2＝（‎3‎‎2‎t）2+（‎3‎‎2‎t﹣3）2，‎ ‎∴t＝3或24（不合题意舍去），‎ ‎∴BP＝6，‎ ‎∴点P（3‎3‎，3），‎ 综上所述：点P坐标为（3‎3‎，3）或（‎7‎‎3‎‎3‎，‎7‎‎3‎）．‎ 第29页（共29页）‎