2011吉林中考数学试卷及答案 11页

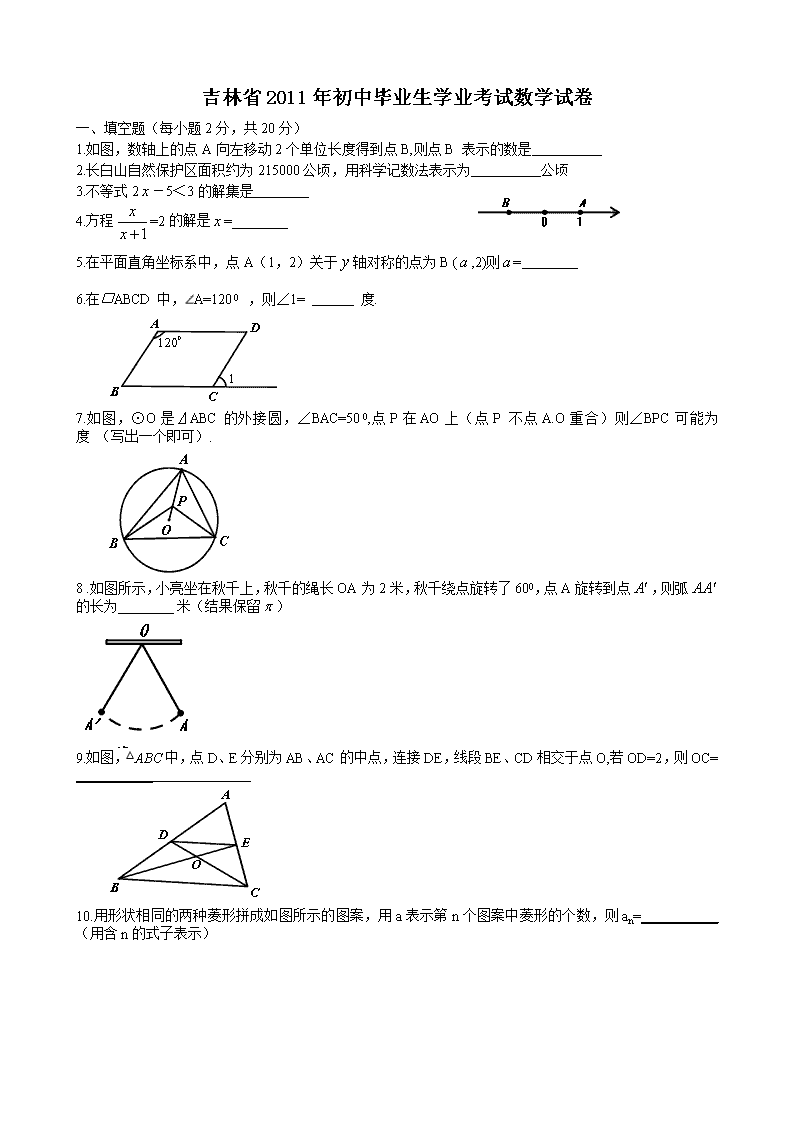
吉林省2011年初中毕业生学业考试数学试卷 一、填空题（每小题2分，共20分）‎ ‎1.如图，数轴上的点A向左移动2个单位长度得到点B,则点B 表示的数是 ‎ ‎2.长白山自然保护区面积约为215000公顷，用科学记数法表示为 公顷 ‎ ‎3.不等式2－5＜3的解集是 .‎ ‎4.方程=2的解是= .‎ ‎5.在平面直角坐标系中，点A（1，2）关于轴对称的点为B (,2)则= .‎ ‎6.在□ABCD中，A=1200 ，则∠1= 度.‎ ‎7.如图，⊙O是⊿ABC的外接圆，∠BAC=500,点P在AO上（点P 不点A.O重合）则∠BPC可能为 度 （写出一个即可）.‎ ‎8 .如图所示，小亮坐在秋千上，秋千的绳长OA为2米，秋千绕点旋转了600，点A旋转到点，则弧的长为 .米（结果保留）‎ ‎9.如图，△ABC中，点D、E分别为AB、AC的中点，连接DE，线段BE、CD相交于点O,若OD=2，则OC= ___________ ‎ ‎10.用形状相同的两种菱形拼成如图所示的图案，用a表示第n个图案中菱形的个数，则an=___________（用含n的式子表示）‎ 二、单项选择题（每小题3分，共18分）‎ ‎11.下列计算正确的是（ ）‎ A a＋2a＝3a2 Ba·a2＝a3 C （2a）2＝2a2 D（－a2）3＝a6‎ ‎12.如图所示，小华看到桌面上的几何体是由五个小正方体组成的，他看到的几何体的主视图是（ ）‎ ‎13.某班九名同学在篮球场进行定点投篮测试，每人投篮子次，投中的次数统计如下：‎ ‎4，3，2，4，4，1，5，0，3，则这级数据的中位数、众数分别为（ ）‎ A 3.4 B 4.3 C 3.3 D 4.4‎ ‎14.某学校准备修建一个面积为200平方米的矩形花圃，它的长比宽多10米，设花圃的宽为米，则可列方程为（ ）‎ A (-10)=200 B 2+2(-10)=200 C (+10)=200 D 2+2(+10)=200 ‎ ‎15.如图，两个等圆⊙A⊙B分别与直线相切于点C、D,连接AB,与直线相交于点O , ‎ ‎∠AOC=300,连接AC.BC,若AB=4，则圆的半径为（ ）‎ ‎ A B 1 C D 2‎ ‎16.如图所示，将一个正方形纸片按下列顺序折叠，然后将最后 折叠的纸片沿虚线去一个三角形和一个形如“1”的图形，将纸片展开，得到的图形是（ ）‎ 三、解答题（每小题5分，共20分）‎ ‎17.先化简－，再选一个合适的值代入求值.‎ ‎18.学校组织各班开展“阳光体育”‎ 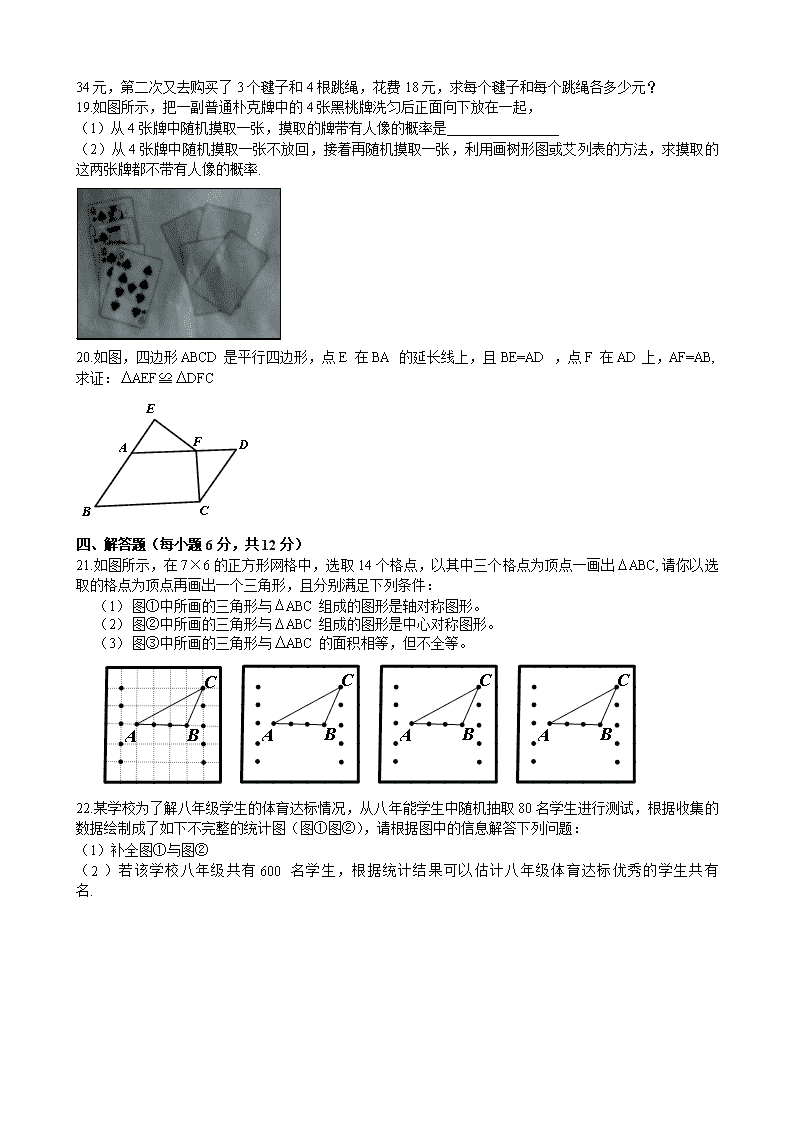活动，某班体育委员第一次到时商店购买了5个毽子和8根跳绳，花费34元，第二次又去购买了3个毽子和4根跳绳，花费18元，求每个毽子和每个跳绳各多少元？‎ ‎19.如图所示，把一副普通朴克牌中的4张黑桃牌洗匀后正面向下放在一起，‎ ‎（1）从4张牌中随机摸取一张，摸取的牌带有人像的概率是________________‎ ‎（2）从4张牌中随机摸取一张不放回，接着再随机摸取一张，利用画树形图或艾列表的方法，求摸取的这两张牌都不带有人像的概率.‎ ‎20.如图，四边形ABCD是平行四边形，点E 在BA 的延长线上，且BE=AD ，点F 在AD上，AF=AB,求证：AEF≌DFC 四、解答题（每小题6分，共12分）‎ ‎21.如图所示，在7×6的正方形网格中，选取14个格点，以其中三个格点为顶点一画出ABC,请你以选取的格点为顶点再画出一个三角形，且分别满足下列条件：‎ （1） 图①中所画的三角形与ABC组成的图形是轴对称图形。‎ （2） 图②中所画的三角形与ABC组成的图形是中心对称图形。‎ （3） 图③中所画的三角形与ABC的面积相等，但不全等。‎ ‎22.某学校为了解八年级学生的体育达标情况，从八年能学生中随机抽取80名学生进行测试，根据收集的数据绘制成了如下不完整的统计图（图①图②），请根据图中的信息解答下列问题：‎ ‎（1）补全图①与图②‎ ‎（2）若该学校八年级共有600名学生，根据统计结果可以估计八年级体育达标优秀的学生共有 名.‎ 图① 图②‎ 五、解答题（每小题7分，共14分）‎ ‎23.如图所示，为求出河对岸两棵树A.B间的距离，小坤在河岸上选取一点C，然后沿垂直于AC的直线的前进了12米到达D，测得∠CDB=900。取CD的中点E，测∠AEC=560, ∠BED=670，求河对岸两树间的距离（提示：过点A作AF⊥BD于点F）(参考数据sin560≈ ,tan560 ≈,sin670≈,tan670≈)‎ ‎24.如图，在平的直角坐标系中，直线 y=-2x+2 与 x轴y轴分别相交于点A,B，四边形ABCD是正方形，曲线y=在第一象限经过点D.‎ ‎(1)求双曲线表示的函数解析式。‎ ‎（2)将正方形ABCD沿X轴向左平移______个单位长度时，点C的对应点恰好落在（1）中的双曲线上 六、解答题（每小题8分，共16分）‎ ‎25.如图，在⊙O中，AB为直径，AC为弦，过点C作CD⊥AB 与点D，将△ACD沿点D落在点E处，AE交⊙O于点F ,连接OC、FC.‎ ‎(1）求证：CE是⊙O的切线。‎ ‎（2）若FC∥AB，求证：四边形 AOCF是菱形。 ‎ ‎26.有甲乙两个均装有进水管和出水管的容器，初始时，两容器同时开进水管，甲容器到8分钟时，关闭进水管打开出水管；到16分钟时，又打开了进水管，此时既进水又出水，到28分钟时，同时关闭两容器的进水管。两容器每分钟进水量与出水量均为常数，容器的水量y(升)与时间 (分)之间的函数关系如图所示，解答下列问题：‎ ‎（1）甲容器的进水管每分钟进水_______升，出水管每分钟出水_____升.‎ ‎（2) 求乙容器内的水量y与时间的函数关系式.‎ ‎（3）求从初始时刻到两容器最后一次水量相等时所需的时间.‎ 六、解答题（每小题10分，共20分）‎ ‎27.如图，抛物线1 :y=-x2平移得到抛物线，且经过点O(0.0)和点A(4.0)，的顶点为点B，它的对称轴与相交于点C,设、与BC围成的阴影部分面积为S,解答下列问题：‎ ‎（1）求表示的函数解析式及它的对称轴，顶点的坐标。‎ ‎（2）求点C的坐标，并直接写出S的值。‎ ‎（3）在直线AC上是否存在点P，使得S△POA＝S？若存在，求点P的坐标；若不存在，请说明理由。‎ ‎【参考公式：抛物线y=ax2+bx+c 的对称轴是x＝－ ，顶点坐标是（－ ，）】．‎ ‎28.如图，梯形ABCD中，AD∥BC,∠BAD=90°，CE⊥AD于点E,AD=8cm，BC=4cm,AB=5cm。从初始时刻开始，动点P,Q 分别从点A,B同时出发，运动速度均为1 cm /s, 动点P沿A-B--C--E的方向运动，到点E停止；动点Q沿B--C--E--D的方向运动，到点D停止，设运动时间为s，PA Q的面积为y cm2，（这里规定：线段是面积为0的三角形)‎ 解答下列问题：‎ ‎(1) 当x=2s时，y=_____ cm2;当= s时，y=_______ cm2 (2）当5 ≤ x ≤ 14 时，求y与之间的函数关系式。‎ ‎(3）当动点P在线段BC上运动时，求出S梯形ABCD时的值。‎ ‎（4）直接写出在整个运动过程中，使PQ与四边形ABCE的对角线平行的所有x的值．‎ 吉林省2011年初中学业考试数学试卷参考答案 一、填空题（每小题2分，共20分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 答案 ‎-1‎ ‎＜4‎ ‎=-2‎ ‎-1‎ 题号 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 ‎60‎ ‎70 （答案不唯一，大于50小于100都可）‎ ‎4‎ 二、选择题（每小题3分，共18分）‎ 题号 ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ ‎16‎ 答案 B A A C B D 三、解答题（每小题5分，共20分）‎ ‎17.解：原式＝－ ‎＝－ ‎＝ 当=2时，原式=1（答案不唯一，取即可）‎ ‎18.解：设每个毽子元，每根跳绳元，根据题意得 ‎ ‎ 解得 答：每个毽子2元，每根跳绳3元.‎ ‎19.解：（1） （2）树形图 ‎ ‎ ‎ ‎9 10 J Q ‎ ‎ ‎10 J Q 9 J Q 9 10 Q 9 10 J 或列表 ‎9‎ ‎10‎ J Q ‎9‎ ‎(10，9)‎ ‎(J，9)‎ ‎(Q，9)‎ ‎10‎ ‎(9，10)‎ ‎(J，10)‎ ‎(Q，10)‎ J ‎(9，J)‎ ‎(10，J)‎ ‎(Q，J)‎ Q ‎(9，Q)‎ ‎(10，Q)‎ ‎(J，Q)‎ 所以P（两张牌都不带有人像）‎ ‎20.证明：∵BE=AD,AF=AB ‎ ∴AE=DF ‎∵四边形ABCD 是平行四边形 ‎∴AB=CD,AB∥CD ‎∴AF=CD, ∠EAF=∠D ‎∴AEF≌DFC 四、解答题（每小题6分，共12分）‎ ‎21.‎ ‎22.‎ ‎（2）180‎ 五、解答题（每小题7分，共14分）‎ ‎23.解：∵E为CD中点，CD=12,‎ ‎∴CE=DE=6.‎ 在Rt⊿ACE中，‎ ‎∵tan56°=‎ ‎∴AC=CE. tan56°≈6×=9‎ ‎ 在Rt△BDE中，∵tan67°=  ，‎ ‎∴BD=DE. tan67°=6×=14  . ‎ ‎∵AF⊥BD ,‎ ‎∴AC=DF=9,AF=CD=12,‎ ‎∴BF=BD-DF=14-9=5.‎ 在Rt⊿AFB中，AF=12,BF=5,‎ ‎∴‎ ‎∴两树间距离为13米。‎ ‎24.解：（1）过点D作DE⊥轴于点E.‎ ‎∵直线y=-2+2与轴，y轴相交于点A.B,‎ ‎∴当=0时，y=2,即OB=2.‎ 当y=0时，=1,即OA=1.‎ ‎∵四边形ABCD是正方形，‎ ‎∴∠BAD=90°，AB=AD.‎ ‎∴∠BAO+∠DAE=90°。‎ ‎∵∠ADE+∠DAE=90°,‎ ‎∴∠BAO=∠ADE ‎∵∠AOB=∠DEA=90°‎ ‎∴⊿AOB ≌ ⊿DEA ‎∴DE=AO=1,AE=BO=2,‎ ‎∴OE=3,DE=1.‎ ‎∴点D 的坐标为（3，1）‎ 把（3，1）代入 y=中，得k=3‎ ‎∴y=‎ ‎（2）1‎ 六、解答题（每小题8分，共16分）‎ ‎25.解： (1）由翻折可知 ∠FAC=∠OAC, ∠E=∠ADC=90° ∵OA=OC, ∴∠OAC=∠OCA ∴∠FAC=∠OCA, ∴OC∥AE ‎∴∠OCE=90°，即OC⊥OE ∴CE是⊙O的切线 （2）∵FC∥AB,OC∥AF, ∴四边形AOCF是平行四边形 ∵OA=OC， ∴□AOCF是菱形 ‎26.解：（1）5,2.5‎ ‎ ‎ 六、解答题（每小题10分，共20分）‎ ‎27. 解：（1）设l2的函数解析式为y＝－x2＋bx＋c 把（4.0）代入函数解析式，得 ‎ 解得 ‎∴y＝－x2＋4x ‎∵y＝－x2＋4x＝－（x－2）2＋4‎ ‎∴l2的对称轴是直线x＝2，顶点坐标B（2，4）‎ ‎（2）当x＝2时，y＝－x2＝－4‎ ‎∴C点坐标是（2，－4）‎ S＝8‎ ‎（3）存在 设直线AC表示的函数解析式为y＝kx＋n 把A（4，0），C（2，－4）代入得 解得 ‎∴y＝2x－8‎ 设△POA的高为h S△POA＝OA·h=2h=4‎ 设点P的坐标为（m,2m-8). ∵S△POA＝S 且S＝8‎ ‎∴S△POA＝×8=4‎ 当点P在轴上方时，得× 4（2m-8)=4,‎ 解得m=5,‎ ‎∴2m-8=2.‎ ‎∴P的坐标为（5.2）.‎ 当点P在轴下方时，得× 4（8-2m)=4.‎ 解得m=3,‎ ‎∴2m-8=-2‎ ‎∴点P的坐标为（3，-2）.‎ 综上所述，点P的坐标为（5，-2）或（3，-2）。‎ ‎28.解：（1） 2；9、 （2） 当5≤≤9时 ‎ y= S梯形ABCQ –S△ABP –S△PCQ =(5+-4)×4×5(-5)(9-)(-4) ‎ ‎ 当9＜≤13时 ‎ y=（-9+4）(14-) ‎ ‎ 当13＜≤14时 ‎ y=×8(14-)=-4+56 即y=-4+56 （3） 当动点P在线段BC上运动时， ∵S梯形ABCD× (4+8)×5 = 8 即²-14+49 = 0 解得1 = 2 = 7 ∴当=7时，S梯形ABCD （4） 说明：（1）自变量取值不含9，13可不扣分.(2）不画草图或草图不正确，可不扣分