2014广西南宁市中考数学试题 10页

2014 广西南宁市初中毕业升学考试试卷 数学 （满分 120 分，考试时间 120 分钟） 一、选择题（本大题共 12 小题，每小题 3分，满分 36 分，在每小题给出的四个 选项中，只有一项是符合题目要求的。） 1.（2014 广西南宁，1，3 分）如果水位升高 3m 时水位变化记作+3m，那么水位 下降 3m 时水位变化记作（ ） A．-3m B．3m C．6m D． -6m 【答案】A 2. （2014 广西南宁，2，3 分）下列图形中，是轴对称图形的是（ ） 【答案】D 3. （2014 广西南宁，3，3 分）南宁东高铁火车站位于南宁市青秀区凤岭北路， 火车站总建筑面积约为 267000 平方米，其中数据 267000 用科学计数法表示 为：（ ） A． 4107.26  B． 41067.2  C． 51067.2  D． 610267.0  【答案】C 4. （2014 广西南宁，4，3分）要使二次根式 2x 在实数范围内有意义，则实 数 x的取值范围是（ ） A． x＞2 B． x≥2 C． x＞-2 D． x≥-2 【答案】D 5. 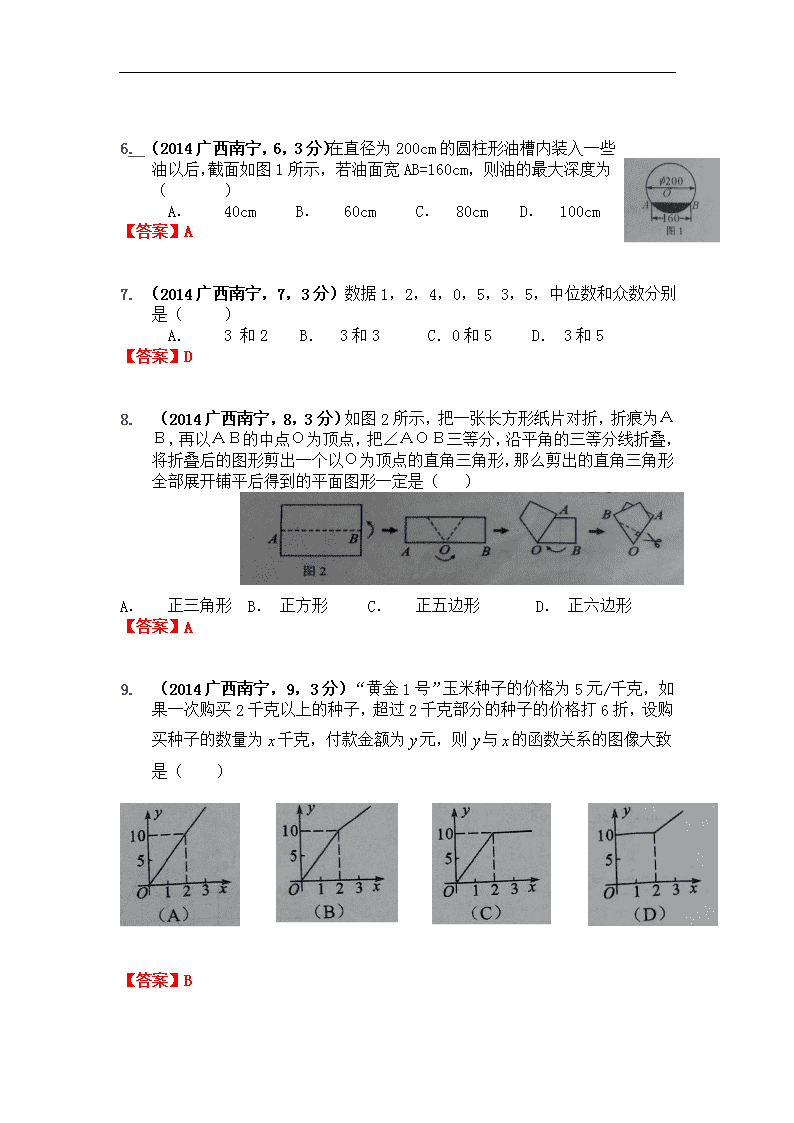（2014 广西南宁，5，3 分）下列运算正确的是（ ） A． 532 aaa  B．   632 xx  C． 326 mmm  D． 246  aa 【答案】B 6. （2014 广西南宁，6，3分）在直径为 200cm 的圆柱形油槽内装入一 些油以后，截面如图 1所示，若油面宽 AB=160cm，则油的最大深 度为（ ） A． 40cm B． 60cm C． 80cm D． 100cm 【答案】A 7. （2014 广西南宁，7，3分）数据 1，2，4，0，5，3，5，中位数和众数分别 是（ ） A． 3 和 2 B． 3 和 3 C．0 和 5 D． 3 和 5 【答案】D 8. jscm（2014 广西南宁，8，3分）如图 2所示，把一张长方形纸片对折，折痕为 ＡＢ，再以ＡＢ的中点Ｏ为顶点，把∠ＡＯＢ三等分，沿平角的三等分线折 叠，将折叠后的图形剪出一个以Ｏ为顶点的直角三角形，那么剪出的直角三 角形全部展开铺平后得到的平面图形一定是（ ） A． 正三角形 B． 正方形 C． 正五边形 D． 正六边形 【答案】A 9. jscm（2014 广西南宁，9，3分）“黄金 1号”玉米种子的价格为 5元/千克， 如果一次购买 2千克以上的种子，超过 2千克部分的种子的价格打 6折，设 购买种子的数量为 x千克，付款金额为 y元，则 y与 x的函数关系的图像大 致是（ ） 【答案】B 10. jscm（2014 广西南宁，10，3 分）如图 3，已知二次函数 xxy 22  ， 当-1＜ x＜ a时， y随 x的增大而增大,则实数 a的取 值范围是（ ） A． a＞1 B．-1＜ a≤1 C． a＞0 D． -1＜ a＜2 【答案】B 11. jscm（2014 广西南宁，11，3 分）如图 4，在□ABCD 中，点 E是 AD 的中点， 延长 BC 到点 F，使 CF：BC=1：2，连接 DF，EC， 若 AB=5，AD=8，sinB= 5 4 ，则 DF 的长等于（ ） A． 10 B． 15 C． 17 D． 52 【答案】C 12. jscm（2014 广西南宁，12，3 分）已知点 A在双曲线 x y 2  上，点 B在直线 4 xy ，且 A，B两点关于 y轴对称，设点 A的坐标为（m，n），则 m n n m  的 值是（ ） A． -10 B． -8 C．6 D． 4 【答案】 A 二、填空题（本大题共 6小题，每小题 3分，满分 18 分.） 13. （2014 广西南宁，13，3 分） 比较大小：-5 3（填“＞”“＜或 “=”）。 【答案】 ＜ 14. （2014 广西南宁，14，3 分）如图 5，已知直线 a∥b，∠1=120°， 则∠2= ° 【答案】 60° 15. （2014 广西南宁，15，3 分）因式分解： aa 62 2  = 【答案】 )3(2 aa 16. （2014 广西南宁，16，3 分）第 45 届世界体操锦标赛将于 2014 年 10 月 3 日至 12 日在南宁市隆重举行，届时某校将从小记者团内负责体育赛事报道 的 3名同学（2男 1女）中任选 2名前往采访，那么选出的 2名同学恰好是 1男 1女的概率是 。 【答案】 3 2 17. （2014 广西南宁，17，3 分）如图 6，一渔船 由西往东航行，在 A点测得海岛 C位于北偏东 60°的方向，前进 20 海里到达 B点，此时， 测得海岛 C位于北偏东 30°的方向，则海岛 C 到航线 AB 的距离 CD 等于 海里。 【答案】 310 18. （2014 广西南宁，18，3 分）如图 7，△ABC 是等腰直角三角形，AC=BC= a， 以斜边 AB 上的点 O为圆心的圆分别与 AC，BC 相切于 E，F，与 AB 分别交于 点 G，H，且 EH 的延长线和 CB 的延长线交于点 D，则 CD 的长为 解：连 OE,OF，则 AO= 2 2 a， HB= 2 2 112 2 2 2a a a a   ，由△HDB∽△HEO， 得 DB HB OE HO ，∵OE=OH，∴DB=BH， ∴DC= 2 1 2 1 2 2a a a   【答案】 a 2 12  三、解答题（本大题共 2小题，每小题 6分，共 12 分） 19. （2014 广西南宁，19，6 分）计算：   45sin1 2  °+ 83  【答案】解： 2 234 223 2 21  原式 20. jscm（2014 广西南宁，20，6 分）解方程： 1 4 2 2 2     xx x 【答案】解：   422 2  xxx 1x 当 1x 时， 042 x ∴ 1x 是原方程的解。 四、（本大题共 2 小题，每小题满分 8分，共 16 分） 21. （2014 广西南宁，21，8 分）如图 8，△ABC 三个顶点的坐标分别是 A（1,1）， B (4,2),C(3,4). (1)请画出△ABC向左平移5个单位长度后得到的△ 111 CBA ； (2)请画出△ABC 关于原点对称的△ 222 CBA (3)在 x轴上求作一点 P，使△PAB 周长最小，请画出△PAB， 并直接写出点 P的坐标。 【答案】解： 如图所示： （1）如图：得到的△ 111 CBA ； （2）如图：△ 222 CBA （3）如画：△PAB， 点 P的坐标是（2,0） 22. （2014 广西南宁，22，8 分）考试前，同学们总会采用各种方式缓解考试压 力，以最佳状态迎接考试。某校对该校九年级的部分同学做了一次内容为“最 适合自己的考前减压方式”的调查活动，学校将减压方式分为五类，同学们 可根据自己的情况必选且只选其中一类。学校收集整理数据后，绘制了图 9-1 和 9-2 两幅不完整的统计图，请根据统计图中的信息解答下列问题： （1）这次抽样调查中，一共抽查了多少名学生？ （2）请补全条形统计图； （3）请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数； （4）根据调查结果，估计该校九年级 500 名学生中采用“听音乐”的减压方式 的人数。 【答案】解： （1）一共抽查的学生人数= 50 16.0 8  （人） （2）如图： 体育活动的人数=50-8-10-12-5=15（人）， （3）“享受美食”所对应扇形的圆心角的度数 =360°× 72 50 10  °， （4）该校九年级 500 名学生中采用“听音乐”的 减压方式的人数=500× 120 50 12  （人） 五、（本大题满分 8 分） 23. （2014 广西南宁，23，9 分）如图 10，, AB∥FC， D 是 AB 上一点，DF 交 AC 于点 E，DE=FE，分别延 长 FD 和 CB 交于点 G。 （1）求证：△ADE≌△CFE； （2）若 GB=2，BC=4，BD=1，求 AB 的长。 【答案】解： （1） 证明： ∵AB∥FC， ∴∠ADE=∠CFC,∠EAD=∠ECF △ADE 和△CFE 中 ∠ADE=∠CFC, DE=FE，∠EAD=∠ECF ∴△ADE≌△CFE. (2) ∵AB∥FC, ∴△GBD≌△GCF, ∴ CF BD GC GB  ∵GB=2，BC=4，BD=1 ∴ CF 1 42 2   ∴CF=3, ∵△ADE≌△CFE, ∴AD=CF=3 ∴AB=BD+AD=1+3=4 六、（本大题满分 10 分） 24. （2014 广西南宁，24，10 分）“保护好环境，拒绝冒黑烟”，某市公交公 司将淘汰某一条线路上“冒黑烟”较严重的公交车，计划购买 A型和 B型两 种环保节能公交车共 10 辆。若购买 A型公交车 1辆，B型公交车 2辆，共 需 400 万元；若购买 A型公交车 2辆，B型公交车 1辆，共需 350 万元。 （1）求购买 A型和 B型公交车每辆各需多少万元？ （2）预计在该线路上 A型和 B型公交车每辆车年均载客量分别为 60 万人次和 100 万人次，若该公司购买 A型和 B型公交车的总费用不超过 1200 万元， 且确保这 10 辆公交车在该线路的年均载客量总和不少于 680 万人次，则该 公司有哪几种购车方案？哪种购车方案的总费用最少？最少总费用是多 少？ 【答案】解： （1） 设购买 A型和 B型公交车每辆各需 x、 y万辆，由题意得：      3502 4002 yx yx ，解得：      150 100 y x 答：购买 A型和 B型公交车每辆各需 100、150 万辆. （2）设购买 A型公交车 m辆,则购买 B型公交车（10-m）辆，由题意得：      680)10(10060 1200)10(150100 mm mm ， 不等式组的解集为： 86  m , ∵m 为正整数， ∴m=6,7,8. ∴购车方案有三种：①A型 6辆；B型 4辆； ②A型 7辆；B型 3辆； ③A型 8辆；B型 2辆； 方案③购车方案最少，最少总费用=1100 万元 七、（本大题满分 10分） 25. （2014 广西南宁，25，10 分）如图 11-1，四边形 ABCD 是正方形，点 E是 边 BC 上一点，点 F在射线 CM 上，∠AEF= 90°，AE=EF，过点 F作射线 BC 的垂线，垂足为 H，连接 AC。 （1）试判断 BE 与 FH 的数量关系，并说明理由。 （2）求证：∠ACF= 90°； （3）连接 AF，过 A,E，F 三点作圆，如图 11-2，若 EC=4，∠CEF=15°，求弧 AE 的长。 【答案】解： （１）证明：BE=FH，理由如下： ∵FH⊥EH，∴∠EHF＝90° ∴∠ABE＝∠EHF=90°，AE=EF， ∵∠BAE＋∠AEB＝90° ∠AEB＋∠FEH＝90° ∴∠BAE＝∠HEF， △ABE≌△EHF， ∴BE=FH， （2）证明： ∵△ABE≌△EHF ∴AB=EH，BE=HF， ∴BE=CH， ∴CH=HF， ∴∠ACD=∠FCH=45°, ∴∠ACF= 90°. （3） ∵∠CEF=15° ∵∠FCH=45° ∴∠CFE=30° 圆心为 O，EO，CO， ∵∠CFE=30° ∴∠EOC=60° ∴EO=EC=4， ∵∠AEF= 90° AE=EF， ∴EO⊥AF，∠AOE= 90° ∴弧 AE 的长=  242 360 90  八、（本大题满分 10分） 26. j（2014 广西南宁，26，12 分）在平面直角坐标系中，抛物线   kxkxy  12 与直线 1 kxy 交于 A，B两点，点 A在点 B的左侧。 （1）如图 12-1，当 1k 时，直接写出 A，B两点的坐标； （2）在（1）的条件下，点 P为抛物线上的一个动点，且在直线 AB 下方，试求 出△ABP 面积的最大值及此时点 P的坐标； （3）如图 12-2，抛物线   kxkxy  12 （ k＞0）与 x轴交于 C，D两点（点 C在点 D的左侧），在直线 1 kxy 上是 否存在唯一一点 Q，使得∠OQC=90°？若存在，请求出此时 k的值，若不存在， 请说明理由。 【答案】解： （1） 当 1k 时，抛物线为： 12  xy ，直线为： 1 xy 它们的交点,      1 12 xy xy ,∴ 11 x ， 22 x ，∴ 01 y ， 32 y ∴A点的坐标（-1,0）；B点的坐标（2,3） （2） △ABP 面积取最大值，即点 P到 AB 的距离最大。 即过点 P的平行于 AB 的直线此时要与抛物线相切， 设过点 P的平行于 AB 的直线解析式为： kxy       kxy xy 12 ， 即关于 x的一元二次方程： 012  kxx 有两个相等的实数解。 △ = 0441  k ∴ 4 5 k 此时， 2 1 21  xx ， 4 3 21  yy ，P点的坐标（ 2 1 , 4 3  ）。 △ ABP 面积= 8 27 （3）∵抛物线   kxkxy  12 （ k＞0）与 x轴交于 C，D两点 ∴   012  kxkx ， 11 x ， kx 2 ， k＞0， ∴C点的坐标（- k ,0）；D点的坐标（1,0）   kxkxy  12 ， 1 kxy