2012年潍坊中考数学试卷 11页

试卷类型：A ‎ 2012年潍坊市初中学业水平考试 ‎ 数 学 试 题 第1卷 (选择题 共36分)‎ 一、选择题(本题共12个小题，在每个小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来。每小题选对得3分，选错、不选或选出的答案超出一个均记0分）‎ ‎1．计算：2-2=( )．‎ A． B． C． D．4‎ ‎2．如果代数式有意义，则x的取值范围是( )．‎ A．x≠3 B．x<‎3 C．x>3 D．x≥3‎ ‎3．某班6名同学参加体能测试的成绩如下(单位：分)：75，95，75，75，80，80．关于这组数据的表述错误的是( )．‎ A．众数是75 B．中位数是‎75 C．平均数是80 D．极差是20‎ ‎4．右图空心圆柱体的主视图的画法正确的是( )．‎ ‎ ‎ ‎5．不等式组的解等于( )．‎ A． 1‎1 C． x<2 D． x<1或x>2‎ ‎6．许多人由于粗心，经常造成水龙头“滴水”或“流水”不断．根据测定，一般情况下一个水龙头“滴水”1个小时可以流掉3．‎5千克水．若1年按365天计算，这个水龙头1年可以流掉( )千克水．(用科学计数法表示，保留3个有效数字)‎ ‎ A．3.1×104 B．0.31×‎105 C．3.06×104 D．3.07×104‎ ‎7．已知两圆半径r1、r2分别是方程菇x2—7x+10=0的两根，两圆的圆心距为7，则两圆 ‎ 的位置关系是( )．‎ ‎ A．相交 B．内切 C．外切 D．外离 ‎8．已知矩形ABCD中，AB=1，在BC上取一点E，沿AE将ΔABE向上折叠，使B点落在AD上的F点，若四边形EFDC与矩形ABCD相似，则AD=( )．‎ ‎ A． B． C . 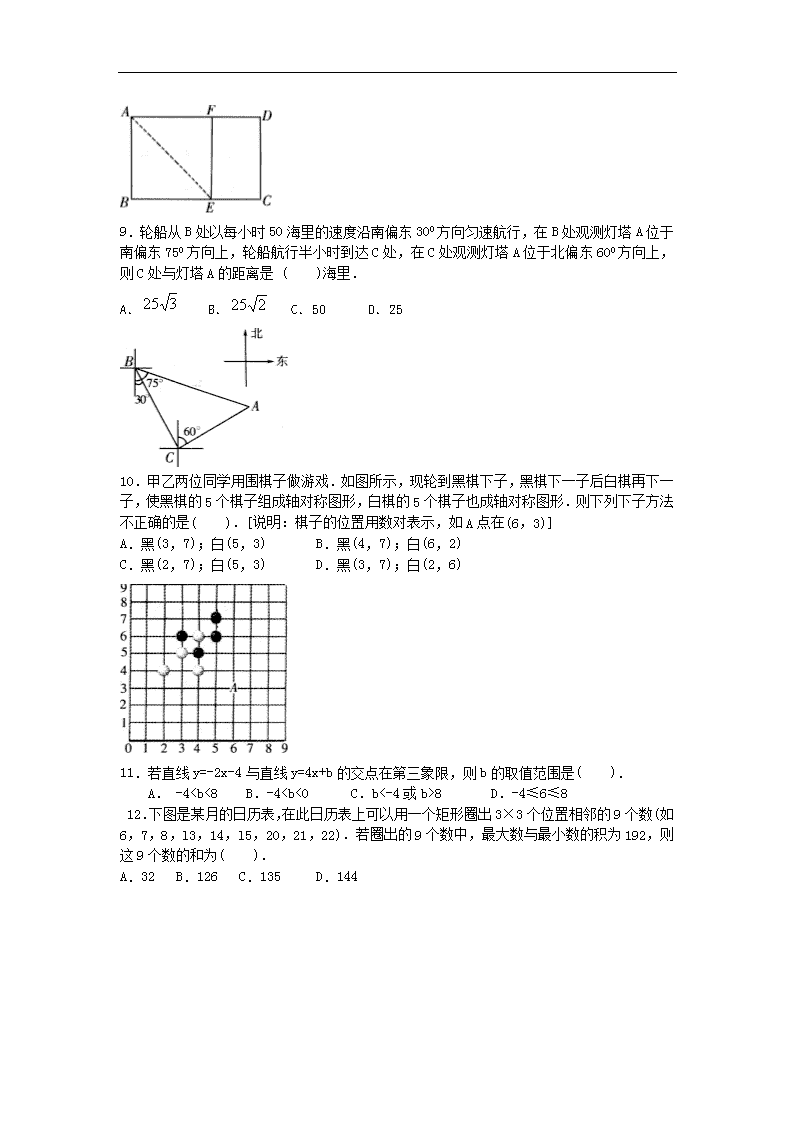D．2‎ ‎9．轮船从B处以每小时50海里的速度沿南偏东300方向匀速航行，在B处观测灯塔A位于南偏东750方向上，轮船航行半小时到达C处，在C处观测灯塔A位于北偏东600方向上，则C处与灯塔A的距离是 ( )海里．‎ A． B． C．50 D．25‎ ‎10．甲乙两位同学用围棋子做游戏．如图所示，现轮到黑棋下子，黑棋下一子后白棋再下一子，使黑棋的5个棋子组成轴对称图形，白棋的5个棋子也成轴对称图形．则下列下子方法不正确的是( )．[说明：棋子的位置用数对表示，如A点在(6，3)]‎ A．黑(3，7)；白(5，3) B．黑(4，7)；白(6，2)‎ C．黑(2，7)；白(5，3) D．黑(3，7)；白(2，6)‎ ‎11．若直线y=-2x-4与直线y=4x+b的交点在第三象限，则b的取值范围是( )．‎ ‎ A． -48 D．-4≤6≤8‎ ‎ 12．下图是某月的日历表，在此日历表上可以用一个矩形圈出3×3个位置相邻的9个数(如6，7，8，l3，14，l5，20，21，22)．若圈出的9个数中，最大数与最小数的积为192，则这9个数的和为( )．‎ A．32 B．‎126 C．135 D．144‎ ‎ 第Ⅱ卷 (非选择题 共84分)‎ 二、填空题(本大题共5个小题，共15分，只要求填写最后结果，每小题填对得3分）‎ ‎13．分解因式：x3—4x2—12x= .‎ ‎14．点P在反比例函数(k≠0)的图象上，点Q(2，4)与点P关于y轴对称，则反比例函数的解析式为 .‎ ‎15．方程的根是 .‎ ‎ ‎ ‎16．如图所示，AB=DB，∠ABD=∠CBE，请你添加一个适当的条件 ， 使ΔABC≌ΔDBE．‎ ‎ (只需添加一个即可)‎ ‎17．右图中每一个小方格的面积为l，则可根据面积计算得到如下算式：1+3+5+7+…+(2n-1)= .(用n表示，n是正整数)‎ 三、解答题(本大题共7个小题，共69分。解答要写必要的文字说明、证明过程或演算步骤.）‎ ‎18．(本题满分9分)‎ ‎ 如图，三角形ABC的两个顶点B、C在圆上，顶点A在圆外，AB、AC分别交圆于E、D两点，连结EC、BD．‎ ‎ (1)求证：ΔABD∽ΔACE；‎ ‎ (2)若ΔBEC与ΔBDC的面积相等，试判定三角形ABC的形状．‎ ‎19．(本题满分9分)为了援助失学儿童，初三学生李明从2012年1月份开始，每月一次将相等数额的零用钱存入已有部分存款的储蓄盒内，准备每6个月一次将储蓄盒内存款一并汇出(汇款手续费不计)．已知2月份存款后清点储蓄盒内有存款80元，5月份存款后清点储蓄盒内有存款125元．‎ ‎ (1)在李明2012年1月份存款前，储蓄盒内已有存款多少元?‎ ‎ (2)为了实现到2015年6月份存款后存款总数超过1000元的目标，李明计划从2013年1月份开始，每月存款都比2012年每月存款多t元(t为整数)，求t的最小值．‎ ‎20．(本题满分l0分)校车安全是近几年社会关注的重大问题，安全隐患主要是超速和超载．某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验：先在公路旁边选取一点C，再在笔直的车道上确定点D，使CD与垂直，测得CD的长等于‎21米，在上点D的同侧取点A、B，使∠CAD=300，∠CBD=600．‎ ‎ (1)求AB的长(精确到‎0.1米，参考数据：)；‎ ‎ (2)已知本路段对校车限速为40千米／小时，若测得某辆校车从A到B用时2秒，这辆校车是否超速?说明理由． ‎ ‎21．(本题满分l0分)田忌赛马的故事为我们所熟知．小亮与小齐学习概率初步知识后设计了如下游戏：小亮手中有方块l0、8、6三张扑克牌，小齐手中有方块9、7、5三张扑克牌．每人从各自手中取一张牌进行比较，数字大的为本“局”获胜，每次取的牌不能放回．‎ ‎(1)若每人随机取手中的一张牌进行比赛，求小齐本“局”获胜的概率；‎ ‎(2)若比赛采用三局两胜制，即胜2局或3局者为本次比赛获胜者．当小亮的三张牌出牌顺序为先出6，再出8，最后出l0时，小齐随机出牌应对，求小齐本次比赛获胜的概率．‎ ‎22．(本题满分l0分)如图，已知平行四边形ABCD，过A作AM⊥BC于M，交BD于E，过C作CN⊥AD于N，交BD于F，连结AF、CE．‎ ‎ (1)求证：四边形AECF为平行四边形；‎ ‎ (2)当AECF为菱形，M点为BC的中点时，求AB：AE的值．‎ ‎23．(本题满分l0分)许多家庭以燃气作为烧水做饭的燃料，节约用气是我们日常生活中非常现实的问题．某款燃气灶旋钮位置从0度到90度(如图)，燃气关闭时，燃气灶旋钮的位置为0度，旋钮角度越大，燃气流量越大，燃气开到最大时，旋钮角度为90度．为测试燃气灶旋钮在不同位置上的燃气用量，在相同条件下，选择在燃气灶旋钮的5个不同位置上分别烧开一壶水(当旋钮角度太小时，其火力不能够将水烧开，故选择旋钮角度x度的范围是18≤x≤90)，记录相关数据得到下表：‎ 旋钮角度(度)‎ ‎ 20‎ ‎ 50‎ ‎ 70‎ ‎ 80‎ ‎ 90‎ 所用燃气量(升)‎ ‎ 73‎ ‎ 67‎ ‎ 83‎ ‎ 97‎ ‎ 115‎ ‎ (1)请你从所学习过的一次函数、反比例函数和二次函数中确定哪种函数能表示 所用燃气量y升与旋钮角度x度的变化规律?说明确定是这种函数而不是其它函数的理由，并求出它的解析式；‎ ‎ (2)当旋钮角度为多少时，烧开一壶水所用燃气量最少?最少是多少?‎ ‎ (3)某家庭使用此款燃气灶，以前习惯把燃气开到最大，现采用最节省燃气的旋钮角度，每月平均能节约燃气10立方米，求该家庭以前每月的平均燃气用量．‎ ‎24．(本题满分11分)如图，已知抛物线与坐标轴分别交于A(-2，O)、B(2，0)、C(0，-l)三点，过坐标原点0的直线y=kx与抛物线交于M、N两点．分别过点C,D(0，-2)作平行于x轴的直线．‎ ‎ (1)求抛物线对应二次函数的解析式；‎ ‎ (2)求证以ON为直径的圆与直线相切；‎ ‎ (3)求线段MN的长(用k表示)，并证明M、N两点到直线的距离之和等于线段MN的长．‎ ‎ 数学试题(A)参考答案及评分标准 一、选择题(本题共l2小题，共36分．在每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来，每小题选对得3分，选错、不选或选出的答案超过一个，均记0分．)‎ 题号 ‎ l ‎ 2‎ ‎ 3‎ ‎ 4‎ ‎ 5‎ ‎ 6‎ ‎ 7‎ ‎ 8‎ ‎ 9‎ ‎ 10‎ ‎ 11‎ ‎ 12 ‎ 答案 ‎ A ‎ C ‎ B ‎ C ‎ A ‎ D ‎ C ‎ B ‎ D ‎ C ‎ A ‎ D ‎ 二、填空题(本题共5小题，共l5分．只要求填写最后结果，每小题填对得3分．)‎ ‎ 13．X(x+2)(x-6) 14. l5．x=30‎ ‎ 16．∠BDE=∠BAC或BE=BC或∠ACB=∠DEB等(写出一个即可．) 17．n2‎ 三．解答题：(本大题共7小题，共69分解答应写出文字说明、证明过程或演算步骤．)‎ ‎ 18。(本题满分9分) ‎ ‎ (1)证明：因为弧ED所对的圆周角相等，所以∠EBD=∠ECD，…………………2分 ‎ 又因为∠A=∠A，所以△ABD∽ΔACE．……………………………………………4分 ‎ (2)法1：因为S△BEC=S△BCD，‎ ‎ S△ACE=S△ABC-S△BEC，S△ABD=S△ABC一S△BCD，………………………………6分 ‎ 所以S△ACE=S△ABD，‎ ‎ 又由(1)知△ABD∽ΔACE，‎ ‎ 所以对应边之比等于1，……………………………………………………………8分 ‎ 所以AB=AC，即三角形ABC为等腰三角形．……………………………………9分 ‎ 法2：因为ΔBEC与ΔBCD的面积相等，有公共底边BC，所以高相等，‎ ‎ 即E、D两点到BC距离相等，所以ED‖BC，……………………………………6分 ‎ 所以∠BCE=∠CED，‎ ‎ 又因为∠CED=∠CBD，‎ ‎ 所以∠BCE=∠CBD，………………………………………………………………8分 ‎ 由(1)知△ABD∽ΔACE，‎ ‎ 所以∠ABD=∠ACE，‎ ‎ 所以∠ABC=∠ACB，‎ ‎ 即三角形ABC为等腰三角形． ……………………………………………………9分 ‎ 19．(本题满分9分)‎ ‎ 解：(1)设李明每月存款x元，储蓄盒内原有存款y元，依题意得，‎ ‎ ....................................................................................2分 ‎ 解得，‎ 所以，储蓄盒内原有存款50元。 …………………………………………………4分 ‎(2)由(1)得，李明2012年共有存款12×15+50=230(元)， …………………5分 ‎2013年1月份后每月存人l5+t(元)，‎ ‎2013年1月到2015年6月共有30个月，…………………………………………6分 依题意得，230+30(15+t)>1000，………………………………………………8分 解得，所以t的最小值为11． ……………………………………………9分 ‎20．(本题满分l0分)‎ 解：(1)由题意得，在RtΔADC中，‎ ‎……………………………．．2分 ‎ ‎ ‎ RtΔBDC 中，…………………．4分 所以AB=AD-BD=36.33‎-12.1l=24.22≈24．2(米)． ………………………6分．‎ ‎(2)汽车从A到B用时2秒，所以速度为24．2÷2=12．1(米/秒)，‎ 因为l2．1×3600=43560，‎ 所以该车速度为43．‎56千米／小时，………………………………………………9分 大于‎40千米／小时，‎ 所以此校车在AB路段超速．……………………………………………………l0分 ‎21．(本题满分l0分)‎ 解：(1)每人随机取一张牌共有9种情况：‎ ‎[或(10，9)，(10，7)，(10，5)，(8，9)，(8，7)，(8，5)，(6，9)，(6，7)，(6，5)]‎ 小齐获胜的情况有(8，9)，(6，9)(6，7)共3种，…………………………………4分 所以小齐获胜的概率为………………………………………………5分 ‎(2)据题意，小明出牌顺序为6、8、10时，‎ 小齐随机出牌的情况有6种情况：‎ ‎(9，7，5)，(9，5，7)，(7，9，5)，(7，5，9)，(5，9，7)，(5，7，9) ……………7分 小齐获胜的情况只有(7，9，5)一种，………………………………………………9分 所以小齐获胜的概率为…………………………………………………l0分 ‎22.(本题满分l0分)‎ ‎(1)证明：因为AE⊥BC，所以∠AMB=900，‎ 因为CN⊥AD，所以∠CNA=900．‎ 又因为BC‖AD，所以∠BCN=900．‎ 所以AE∥CF，………………………………………………………………………2分 又由平行得∠ADE=∠CBD，又AD=BC，‎ 所以ΔADE≌△BCF，‎ 所以AE=CF，‎ 所以四边形AECF为平行四边形．…………………………………………………4分 ‎(2)当AECF为菱形时，连结AC交BF于点0，‎ 则AC与EF互相垂直平分，‎ 又BO=OD，‎ 所以AC与BD互相垂直平分，‎ 所以，四边形ABCD是菱形，……………………6分 所以AB=BC.‎ 因为M是BC的中点，AM⊥BC，‎ 所以，ΔABM≌ΔCAM，‎ 所以，AB=AC，‎ ΔABC为等边三角形，‎ ‎∠ABC=600，∠CBD=300． ………………………………………………………8分 在RtΔBCF中， ‎ CF：BC=tan∠CBF=，‎ 又AE=CF，AB=BC， ‎ 所以AB：AE=…………………………………………………………………l0分 ‎23．(本题满分l0分)‎ 解．(1)若设y=kx+b(k≠0)，由 ，解得 所以，把x=70代人得y=65≠83，所以不符合；………………l分 若设， ，解得k=1460，‎ 所以，把x=50代入得 y=29．2≠67，所以不符合；………………2分 ‎ 若设y=ax2+bx+c，则由，解得 ‎ ‎ ‎ 所以(18≤x≤90)．……………………………………………4分 ‎ 把x=80代入得y=97，把x=90代入得y=115，符合题意．‎ ‎ 所以选用二次函数能表示所用燃气量y升与旋钮角度x度的变化规律．………5分 ‎ (2)由(1)得，……………………………6分 ‎ 所以当x=40时，y取得最小值65．‎ ‎ 即当旋钮角度为40度时，烧开一壶水所用燃气量最少，最少为‎65升．…………8分 ‎ (3)由(2)及表格知，采用最节省燃气的旋钮角度40度比把燃气开到最大时烧开一 壶水节约用气ll5—65=50(升)，‎ ‎ 设该家庭以前每月平均用气量为a立方米，则由题意得，‎ ‎ 解得a=23(立方米)，‎ ‎ 即该家庭以前每月平均用气量为23立方米……………………………………10分 ‎ 24．(本题满分ll分)‎ ‎ 解：(1)设抛物线对应二次函数的解析式为y=ax2+bx+c，‎ 由 解得 ‎ 所以．………………………………………………………3分 ‎ (2)设M(x1，y1)，N(x2，y2)，因为点M、N在抛物线上，‎ ‎ 所以，所以x22=4(y2+1)；‎ ‎ 又ON2=x22+y22=4(y2+1)+y22=(y2+2)2，所以ON=，又因为y2≥-l，‎ ‎ 所以0N=2+y2．………………………………………5分 ‎ 设ON的中点E，分别过点N、E向直线作垂线，垂足为P、F，‎ ‎ 则 ，‎ ‎ 所以ON=2EF，‎ ‎ 即ON的中点到直线，的距离等于0N长度的一半，‎ ‎ 所以以ON为直径的圆与相切．………………………………………7分 ‎(3)过点M作MH⊥NP交NP于点H，则MN2=MH2+NH2=(x2-x1)2+(y2-y1)，‎ 又y1=kx1,y2=kx2，所以（y2-y1)2=k2(x2-x1)2‎ 所以MN2=(1+k2)(x2一xl)2；‎ 又因为点M、N既在y=kx的图象上又在抛物线上，‎ 所以，即x2-4kx-4=0，‎ 所以，‎ 所以(x2-x1)2=16(1+k2)，‎ 所以MN2=16(1+k2)2，∴MN=4(1+k2)…9分 延长NP交于点Q，过点M作MS⊥交于点S，‎ 则MS+NQ=y1+2+y2+2=‎ ‎ 又x12+x22=2[4k2+4(1+k2)]=16k2+8，‎ ‎ 所以MS+NQ=4k2+2+2=4(1+k2)=MN ‎ 即M、N两点到距离之和等于线段MN的长．……………………ll分 ‎ 说明：本参考答案给出了一种解题方法，其它正确方法应参考本标准给出相应分数.‎