- 346.50 KB
- 2021-05-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
旋转提升专题
知识点一 旋转构造全等
几何变换——旋转
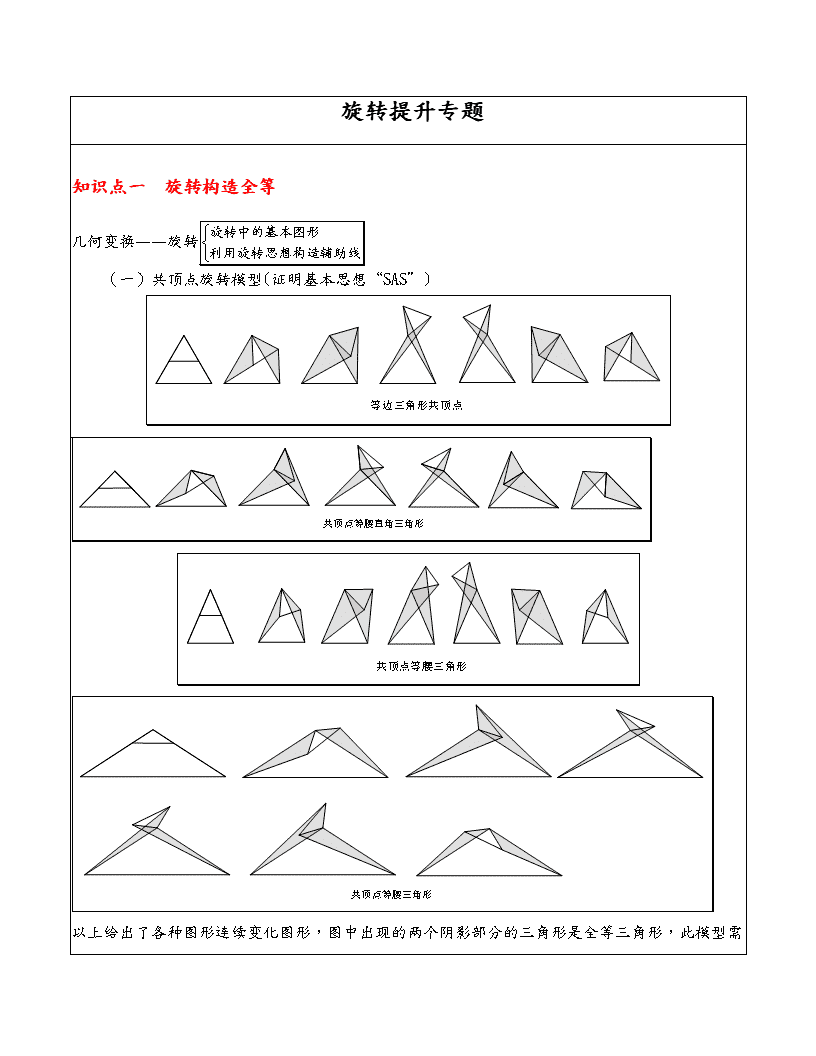
(一)共顶点旋转模型(证明基本思想“SAS”)
以上给出了各种图形连续变化图形,图中出现的两个阴影部分的三角形是全等三角形,此模型需要注意的是利用“全等三角形”的性质进行边与角的转化
二利用旋转思想构造辅助线
(1)根据相等的边先找出被旋转的三角形
(2)根据对应边找出旋转角度
(3)根据旋转角度画出对应的旋转的三角形
三 旋转变换前后具有以下性质:
(1)对应线段相等,对应角相等
(2)对应点位置的排列次序相同
(3)任意两条对应线段所在直线的夹角都等于旋转角.
【例题精讲】
例1.在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P,若SABCD=25,求DP的长。
例2.如图,四边形是正方形,是等边三角形,为对角线上任意一点,将绕点逆时针旋转得到,连接、、.
⑴求证:
⑵①当点在何处时,的值最小;
②当点在何处时,的值最小,并说明理由;
⑶当的最小值为时,求正方形的边长.
方法总结:
1、共顶点的等线段中,最常用旋转思路,但也不可以思维定势,辅助线叙述中用一般语言
2、旋转变换还用于处理:
①几何最值问题:几何最值两个重要公理依据是:两点之间线段最短和垂线段最短;
②有关线段的不等关系;
③自己构造绕某点旋转某角度(特别是60
度),把共顶点的几条线段变为首尾相接的几条线段,再变为共线取得最小值问题,计算中常用到等腰三角形或勾股定理等知识。
【课堂练习】
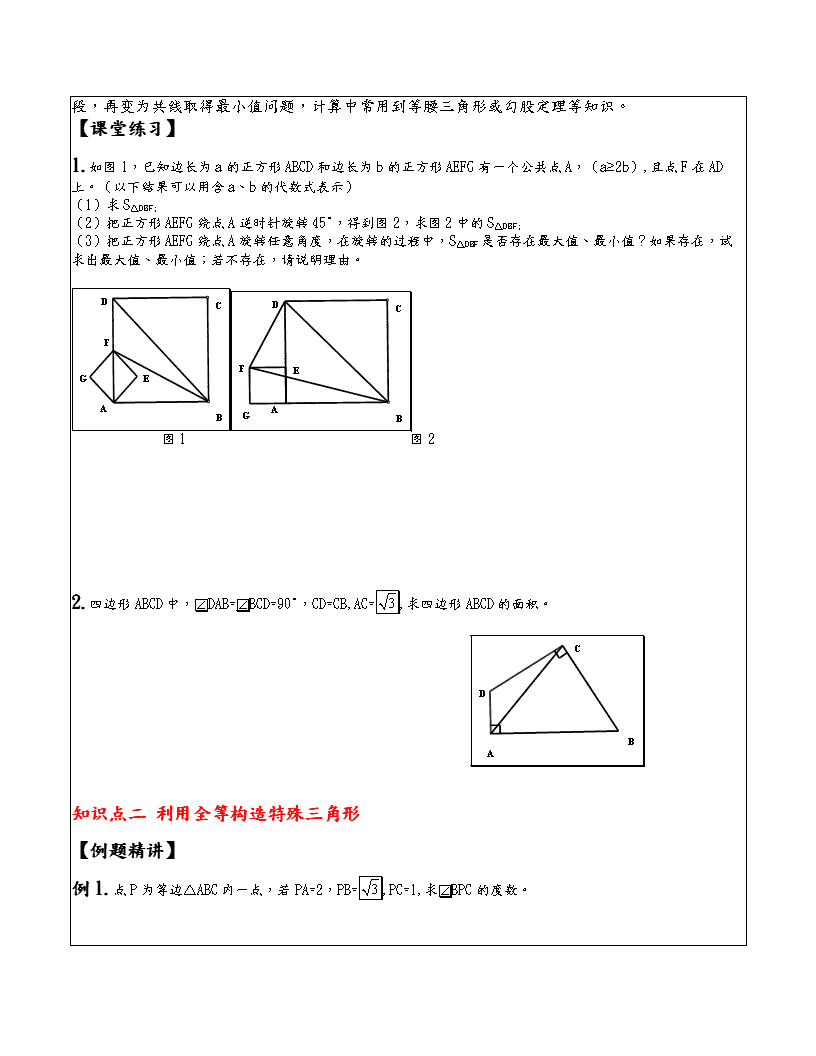
1.如图1,已知边长为a的正方形ABCD和边长为b的正方形AEFG有一个公共点A,(a≥2b),且点F在AD上。(以下结果可以用含a、b的代数式表示)
(1)求S△DBF;
(2)把正方形AEFG绕点A逆时针旋转45°,得到图2,求图2中的S△DBF;
(3)把正方形AEFG绕点A旋转任意角度,在旋转的过程中,S△DBF是否存在最大值、最小值?如果存在,试求出最大值、最小值;若不存在,请说明理由。
图1 图2
2.四边形ABCD中,DAB=BCD=90°,CD=CB,AC=,求四边形ABCD的面积。
知识点二 利用全等构造特殊三角形
【例题精讲】
例1.点P为等边△ABC内一点,若PA=2,PB=,PC=1,求BPC的度数。
例2.图,点P为正方形ABCD内一点,若PA=2,PB=4,APB=135°,求PC 的长。
1.如图,在△ABC中,A=90°,AB=AC,D是斜边BC 上一点,求证:BD2+CD2=2AD2
2.如图,正方形ABCD边长为3,点E、F分别在边BC、CD上且EAF=45°
,求△CEF的周长。
知识点三(知识点名称)
【例题精讲】1.
例2.
1.
2.
3.
旋转的性质,利用旋转构造全等,利用全等构造特殊三角形。
额外拓展:
如图,已知抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,该抛物线顶点为D,对称轴交x轴于点H。
(1) 求A,B两点的坐标;
(2) 设点P在x轴下方的抛物线上,当∠ABP=∠CDB时,求出点P的坐标;
(3) 以OB为边在第四象限内作等边△OBM,设点E为x轴的正半轴上一动点(OE>OH),连接ME,把线段ME绕点M顺时针旋转60°得MF,求线段DF的长的最小值。
1、如图,四边形OABC和ODEF都是正方形,CF交OA于点P,交DA于点Q.
(1) 求证:AD=CF
(2)AD与CF垂直吗?说说你的理由;
(3)当正方形ODEF绕O点在平面内旋转时,(1)、(2)的结论是否有变化?为什么?
2.已知菱形ABCD中,B=60°,若EAF=60°.求证:△AEF是等边三角形。
3.已知正方形ABCD内一点,P到A、B、 C三点的距离之和最小值为+,求此正方形的边长。