嘉兴市2015年中考数学卷 9页

浙江省嘉兴市2015年中考数学试卷 卷Ι（选择题）‎ 一、选择题（本题有10小题，每小题4分，共40分，请选出各题中唯一的正确选项，不选，多选，错选，均不得分）‎ ‎1.计算2-3的结果为（▲）‎ ‎（A）-1 （B）-2 （C）1 （D）2‎ ‎2.下列四个图形分别是四届国际数学家大会的会标，其中属于中心对称图形的有（▲）‎ ‎ ‎ ‎ （A）1个 （B）2个 （C）3个 （D）4个 ‎3.2014年嘉兴市地区生产总值为335 280 000 000元，该数据用科学记数法表示为（▲）‎ ‎（A）33528×107 （B）0.33528×1012‎ ‎（C）3.3528×1010 （D）3.3528×1011‎ ‎4.质检部门为了检测某品牌电器的质量，从同一批次共10 000件产品中随机抽取100件进行检测，检测出次品5件。由此估计这一批次产品中的次品件数是（▲）‎ ‎（A）5 （B）100 （C）500 （D）10 000‎ ‎5.如图，直线l1// l2// l3，直线AC分别交l1， l2， l3于点A，B，C；直线DF分别交l1， l2， l3于点D，E，F .AC与DF相较于点H，且AH=2，HB=1，BC=5，则 的值为（▲）‎ ‎（A） （B）2‎ ‎（C） （D） ‎6.与无理数最接近的整数是（▲）‎ ‎（A）4 （B）5‎ ‎（C）6 （D）7‎ ‎7.如图，中，AB=5，BC=3，AC=4，以点C为圆心的圆与AB相切，则☉C的 半径为（▲）‎ ‎（A）2.3 （B）2.4‎ ‎（C）2.5 （D）2.6‎ ‎8.一元一次不等式2（x+1）≥4的解在数轴上表示为（▲）‎ ‎9.数学活动课上，四位同学围绕作图问题：“如图，已知直线l和l外一点P，用直尺和圆规作直线PQ，使PQ⊥l与点Q .”分别作出了下列四个图形. 其中做法错误的是（▲）‎ ‎ ‎ ‎10.如图，抛物线y=-x2+2x+m+1交x轴于点A（a，0）和B（B，0），交y轴于点C，‎ 抛物线的顶点为D.下列四个判断：①当x>0时，y>0；②若a=-1，则b=4；③抛物 线上有两点P（x1,y1）和Q（x2,y2），若x1<1< x2，且x1+ x2>2，则y1> y2；④点C关于 抛物线对称轴的对称点为E，点G，F分别在x轴和y轴上，当m=2时，四边形EDFG 周长的最小值为，其中正确判断的序号是（▲）‎ ‎（A）① （B）②‎ ‎（C）③ （D）④‎ 卷Ⅱ（非选择题）‎ 二、填空题（本题有6小题，每小题5分，共30分）‎ ‎11.因式分解：ab – a=____▲____.‎ ‎12.右图是百度地图的一部分（比例尺1:4 000 000）.按图可估测杭州 在嘉兴的南偏西____▲____度方向上，到嘉兴的实际距离约为____▲____.‎ ‎13.把一枚均匀的硬币连续抛掷两次，两次正面朝上的概率是____▲____.‎ ‎14.如图，一张三角形纸片ABC，AB=AC=5.折叠该纸片使点A落在边BC 的中点上，折痕经过AC上的点E，则线段AE的长为____▲____.‎ ‎15.公元前1700年的古埃及纸草书中，记载着一个数学问题：“它的全部，‎ 加上它的七分之一，其和等于19.”此问题中“它”的值为____▲____. 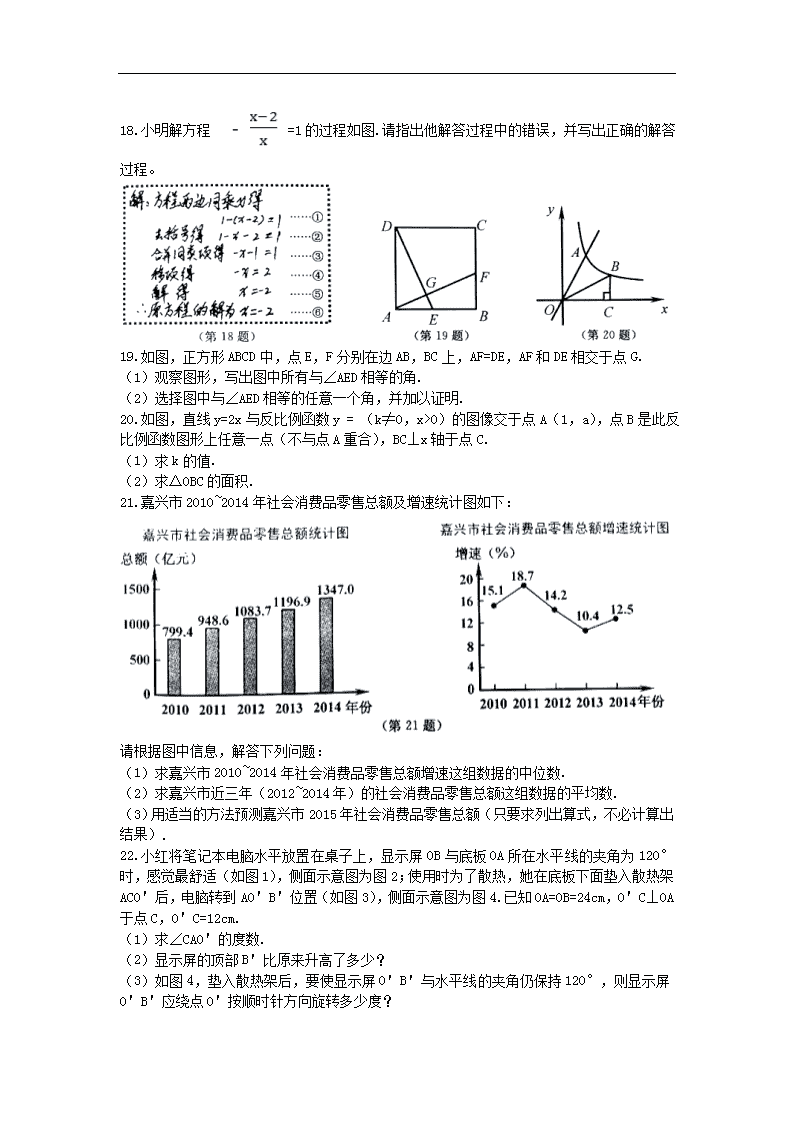‎ ‎16.如图，在直角坐标系xOy中，已知点A（0,1），点P在线段OA上，以 AP为半径的☉P周长为1.点M从A开始沿☉P按逆时针方向转动，射线 AM交x轴于点N（n，0），设点M转过的路程为m（00）的图像交于点A（1，a），点B是此反比例函数图形上任意一点（不与点A重合），BC⊥x轴于点C.‎ ‎（1）求k的值.‎ ‎（2）求△OBC的面积.‎ ‎21.嘉兴市2010~2014年社会消费品零售总额及增速统计图如下：‎ 请根据图中信息，解答下列问题：‎ ‎（1）求嘉兴市2010~2014年社会消费品零售总额增速这组数据的中位数.‎ ‎（2）求嘉兴市近三年（2012~2014年）的社会消费品零售总额这组数据的平均数.‎ ‎（3）用适当的方法预测嘉兴市2015年社会消费品零售总额（只要求列出算式，不必计算出结果）.‎ ‎22.小红将笔记本电脑水平放置在桌子上，显示屏OB与底板OA所在水平线的夹角为120°时，感觉最舒适（如图1），侧面示意图为图2；使用时为了散热，她在底板下面垫入散热架ACO＇后，电脑转到AO＇B＇位置（如图3），侧面示意图为图4.已知OA=OB=24cm，O＇C⊥OA于点C，O＇C=12cm.‎ ‎（1）求∠CAO＇的度数.‎ ‎（2）显示屏的顶部B＇比原来升高了多少？‎ ‎（3）如图4，垫入散热架后，要使显示屏O＇B＇与水平线的夹角仍保持120°，则显示屏O＇B＇应绕点O＇按顺时针方向旋转多少度？‎ ‎23.某企业接到一批粽子生产任务，按要求在15天内完成，约定这批粽子的出厂价为每只6元.为按时完成任务，该企业招收了新工人.设新工人李明第X天生产的粽子数量为y只，y与x满足如下关系： ‎（1）李明第几天生产的粽子数量为420只？‎ ‎（2）如图，设第x天每只粽子的成本是p元，p与x之间的关系 可用图中的函数图形来刻画.若李明第x天创造的利润为w元，求 w关于x的函数表达式，并求出第几天的利润最大，最大利润时多 少元？（利润=出厂价-成本）‎ ‎24.类比等腰三角形的定义，我们定义：有一组邻边相等的凸四边形叫做“等邻边四边形”.‎ ‎（1）概念理解 如图1，在四边形ABCD中，添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.‎ ‎（2）问题探究 ‎ ‎ ①小红猜想：对角线互相平分的“等邻边四边形”是菱形.她的猜想正确吗？请说明理由。‎ ‎ ②如图2，小红画了一个Rt△ABC，其中∠ABC=90°，AB=2，BC=1，并将Rt△ABC沿 ‎∠ABC的平分线BB＇方向平移得到△A＇B＇C＇，连结AA＇，BC＇.小红要是平移后的四边形ABC＇A＇是“等邻边四边形”，应平移多少距离（即线段BB＇的长）？‎ ‎（3）应用拓展 ‎ 如图3，“等邻边四边形”ABCD中，AB=AD，∠BAD+∠BCD==90°，AC，BD为对角线，AC=AB.试探究BC，CD，BD的数量关系.‎ ‎ 参考答案 ‎1-10、ABDCD CBAAC ‎11、a（b﹣1）‎ ‎12、45，160km ‎13、‎ ‎14、2.5‎ ‎15、‎ ‎16、-1 ‎ ‎17、6，2a-1‎ ‎18、解：小明的解法有三处错误，步骤①去分母有误； 步骤②去括号有误；步骤⑥少检验；‎ 正确解法为：方程两边乘以x，得：1﹣（x﹣2）=x，‎ 去括号得：1﹣x+2=x，‎ 移项得：﹣x﹣x=﹣1﹣2，‎ 合并同类项得：﹣2x=﹣3，‎ 解得：x=，‎ 经检验x=是分式方程的解，‎ 则方程的解为x=．‎ ‎19、解：（1）由图可知，∠DAG，∠AFB，∠CDE与∠AED相等；‎ ‎（2）选择∠DAG=∠AED，证明如下：‎ ‎∵正方形ABCD，‎ ‎∴∠DAB=∠B=90°，AD=AB，‎ ‎∵AF=DE，‎ 在△DAE与△ABF中，‎ ‎，‎ ‎∴△DAE≌△ABF（SAS），‎ ‎∴∠ADE=∠BAF，‎ ‎∵∠DAG+∠BAF=90°，∠GDA+∠AED=90°，‎ ‎∴∠DAG=∠AED．‎ ‎20、解：（1）∵直线y=2x与反比例函数y=（k≠0，x＞0）的图象交于点A（1，a），先 ‎∴将A（1，a）代入直线y=2x，得：‎ a=2‎ ‎∴A（1，2），‎ 将A（1，2）代入反比例函数y=中得：k=2，‎ ‎∴y=；‎ ‎（2）∵B是反比例函数y=图象上的点，且BC⊥x轴于点C，‎ ‎∴△BOC的面积=|k|=×2=1．‎ ‎21、解：（1）数据从小到大排列10.4%，12.5%，14.2%，15.1%，18.7%，‎ 则嘉兴市2010～2014年社会消费品零售总额增速这组数据的中位数14.2%；‎ ‎（2）嘉兴市近三年（2012～2014年）的社会消费品零售总额这组数据的平均数是：‎ ‎（799.4+948.6+1083.7+1196.9+1347.0）÷5=1075.12（亿元）；‎ ‎（3）从增速中位数分析，嘉兴市2015年社会消费品零售总额为1347×（1+14.2%）=1538.274（亿元）．‎ ‎22、解：（1）∵O′C⊥OA于C，OA=OB=24cm，‎ ‎∴sin∠CAO′=，‎ ‎∴∠CAO′=30°；‎ ‎（2）过点B作BD⊥AO交AO的延长线于D，‎ ‎∵sin∠BOD=，‎ ‎∴BD=OB•sin∠BOD，‎ ‎∵∠AOB=120°，‎ ‎∴∠BOD=60°，‎ ‎∴BD=OB•sin∠BOD=24×=12，‎ ‎∵O′C⊥OA，∠CAO′=30°，‎ ‎∴∠AO′C=60°，‎ ‎∵∠AO′B′=120°，‎ ‎∴∠AO′B′+∠AO′C=180°，‎ ‎∴O′B′+O′C﹣BD=24+12﹣12=3﹣12，‎ ‎∴显示屏的顶部B′比原来升高了（36﹣12）cm；‎ ‎（3）显示屏O′B′应绕点O′按顺时针方向旋转30°，‎ 理由；∵显示屏O′B与水平线的夹角仍保持120°，‎ ‎∴∠EO′F=120°，‎ ‎∴∠FO′A=∠CAO′=30°，‎ ‎∵∠AO′B′=120°，‎ ‎∴∠EO′B′=∠FO′A=30°，‎ ‎∴显示屏O′B′应绕点O′按顺时针方向旋转30°．‎ ‎23、解：（1）设李明第n天生产的粽子数量为420只，‎ 由题意可知：30n+120=420，‎ 解得n=10．‎ 答：第10天生产的粽子数量为420只．‎ ‎（2）由图象得，当0≤x≤9时，p=4.1；‎ 当9≤x≤15时，设P=kx+b，‎ 把点（9，4.1），（15，4.7）代入得，，‎ 解得，‎ ‎∴p=0.1x+3.2，‎ ‎①0≤x≤5时，w=（6﹣4.1）×54x=102.6x，当x=5时，w最大=513（元）；‎ ‎②5＜x≤9时，w=（6﹣4.1）×（30x+120）=57x+228，‎ ‎∵x是整数，‎ ‎∴当x=9时，w最大=714（元）；‎ ‎③9＜x≤15时，w=（6﹣0.1x﹣3.2）×（30x+120）=﹣3x2+72x+336，‎ ‎∵a=﹣3＜0，‎ ‎∴当x=﹣=12时，w最大=768（元）；‎ 综上，当x=12时，w有最大值，最大值为768．‎ ‎24、解：（1）AB=BC或BC=CD或CD=AD或AD=AB（任写一个即可）；‎ ‎（2）①正确，理由为：‎ ‎∵四边形的对角线互相平分，∴这个四边形是平行四边形，‎ ‎∵四边形是“等邻边四边形”，∴这个四边形有一组邻边相等，‎ ‎∴这个“等邻边四边形”是菱形；‎ ‎②∵∠ABC=90°，AB=2，BC=1，‎ ‎∴AC=，‎ ‎∵将Rt△ABC平移得到△A′B′C′，‎ ‎∴BB′=AA′，A′B′∥AB，A′B′=AB=2，B′C′=BC=1，A′C′=AC=，‎ ‎（I）如图1，当AA′=AB时，BB′=AA′=AB=2；‎ ‎（II）如图2，当AA′=A′C′时，BB′=AA′=A′C′=；‎ ‎（III）当A′C′=BC′=时，‎ 如图3，延长C′B′交AB于点D，则C′B′⊥AB，‎ ‎∵BB′平分∠ABC，‎ ‎∴∠ABB′=∠ABC=45°，‎ ‎∴∠BB′D=′∠ABB′=45°，‎ ‎∴B′D=B，‎ 设B′D=BD=x，‎ 则C′D=x+1，BB′=x，‎ ‎∵在Rt△BC′D中，BD2+（C′D）2=（BC′）2‎ ‎∴x2+（x+1）2=（）2，‎ 解得：x1=1，x2=﹣2（不合题意，舍去），‎ ‎∴BB′=x=，‎ ‎（Ⅳ）当BC′=AB=2时，如图4，‎ 与（Ⅲ）方法一同理可得：BD2+（C′D）2=（BC′）2，‎ 设B′D=BD=x，‎ 则x2+（x+1）2=22，‎ 解得：x1=，x2=（不合题意，舍去），‎ ‎∴BB′=x=；‎ ‎（3）BC，CD，BD的数量关系为：BC2+CD2=2BD2，如图5，‎ ‎∵AB=AD，‎ ‎∴将△ADC绕点A旋转到△ABF，连接CF，‎ ‎∴△ABF≌△ADC，‎ ‎∴∠ABF=∠ADC，∠BAF=∠DAC，AF=AC，FB=CD，‎ ‎∴∠BAD=∠CAF，==1，‎ ‎∴△ACF∽△ABD，‎ ‎∴==，∴BD，‎ ‎∵∠BAD+∠ADC+∠BCD+∠ABC=360°，‎ ‎∴∠ABC+∠ADC﹣360°﹣（∠BAD+∠BCD）=360°﹣90°=270°，‎ ‎∴∠ABC+∠ABF=270°，‎ ‎∴∠CBF=90°，‎ ‎∴BC2+FB2﹣CF2=（BD）2=2BD2，‎ ‎∴BC2+CD2=2BD2．‎