中考数学复习专题代数式 7页

中考数学复习专题 代数式 一. 教学目标：‎ ‎1. 复习整式的有关概念，整式的运算 ‎2. 理解因式分解的概念，掌握提取公因式法、公式法、分组分解法等因式分解方法，能把简单多项式分解因式。‎ ‎3. 掌握分式的概念、性质，掌握分式的约分、通分、混合运算。‎ ‎4. 理解平方根、立方根、算术平方根的概念，会用根号表示数的平方根、立方根和算术平方根。会求实数的平方根、算术平方根和立方根，了解二次根式、最简二次根式、同类二次根式的概念，会辨别最简二次根式和同类二次根式。掌握二次根式的性质，会化简简单的二次根式，能根据指定字母的取值范围将二次根式化简；掌握二次根式的运算法则，能进行二次根式的加减乘除四则运算，会进行简单的分母有理化。‎ 二. 教学重点、难点：‎ 因式分解法在整式、分式、二次根式的化简与混合运算中的综合运用。‎ 三.知识要点：‎ 知识点1 整式的概念 ‎（1）整式中只含有一项的是单项式，否则是多项式，单独的字母或常数是单项式；‎ ‎（2）单项式的次数是所有字母的指数之和；‎ 多项式的次数是多项式中最高次项的次数；‎ ‎（3）单项式的系数，多项式中的每一项的系数均包括它前面的符号 ‎（4）同类项概念的两个相同与两个无关：‎ ‎ 两个相同：一是所含字母相同，二是相同字母的指数相同；‎ ‎ 两个无关：一是与系数的大小无关，二是与字母的顺序无关；‎ ‎（5）整式加减的实质是合并同类项；‎ ‎（6）因式分解与整式乘法的过程恰为相反。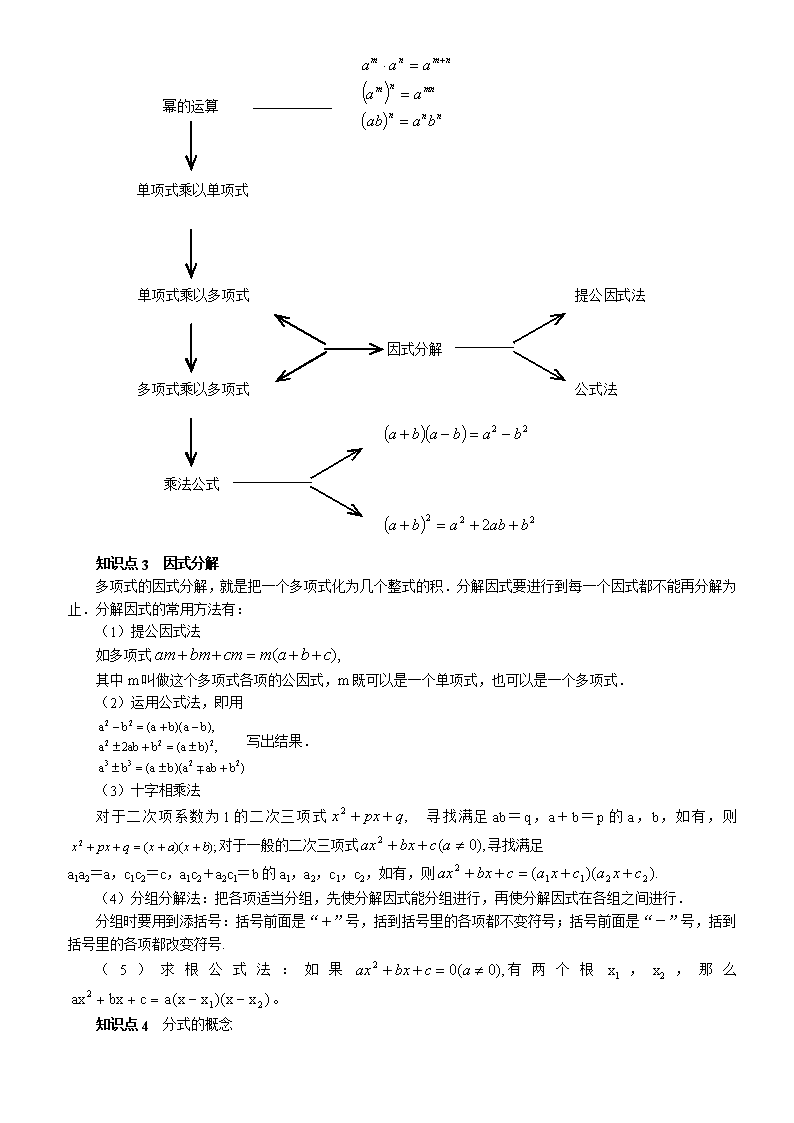‎ 知识点2 整式的运算 （如结构图）‎ 知识点3 因式分解 ‎ 多项式的因式分解，就是把一个多项式化为几个整式的积．分解因式要进行到每一个因式都不能再分解为止．分解因式的常用方法有：‎ ‎ （1）提公因式法 ‎ 如多项式 其中m叫做这个多项式各项的公因式，m既可以是一个单项式，也可以是一个多项式．‎ ‎ （2）运用公式法，即用 ‎ 写出结果．‎ ‎ （3）十字相乘法 对于二次项系数为l的二次三项式 寻找满足ab＝q，a＋b＝p的a，b，如有，则对于一般的二次三项式寻找满足 a‎1a2＝a，c‎1c2＝c，a‎1c2＋a‎2c1＝b的a1，a2，c1，c2，如有，则 ‎（4）分组分解法：把各项适当分组，先使分解因式能分组进行，再使分解因式在各组之间进行．‎ 分组时要用到添括号：括号前面是“＋”号，括到括号里的各项都不变符号；括号前面是“－”号，括到括号里的各项都改变符号.‎ ‎（5）求根公式法：如果有两个根x1，x2，那么。‎ 知识点4 分式的概念 ‎（1）分式的定义：整式A除以整式B，可以表示成的形式。如果除式B中含有字母，那么称为分式，其中A称为分式的分子，B为分式的分母。‎ 对于任意一个分式，分母都不能为零。‎ ‎（2）分式的约分 ‎（3）分式的通分 知识点5 分式的性质 ‎（1）（2）已知分式，分式的值为正：a与b同号；分式的值为负：a与b异号；分式的值为零：a＝0且b0；分式有意义：b0。‎ ‎（3）零指数 ‎ ‎（4）负整数指数 ‎ ‎（5）整数幂的运算性质 ‎ 上述等式中的m、n可以是0或负整数．‎ 知识点6 根式的有关概念 ‎1. 平方根：若x2＝a（a>0），则x叫做a的平方根，记为。‎ 注意：①正数的平方根有两个，它们互为相反数；②0的平方根是0；③负数没有平方根；‎ ‎2. 算术平方根：一个数的正的平方根叫做算术平方根；‎ ‎3. 立方根：若x3＝a（a>0），则x叫做a的立方根，记为。‎ ‎4. 最简二次根式 ‎ 被开方数所含因数是整数，因式是整式，不含能开得尽方的因数或因式的二次根式，叫做最简二次根式。‎ ‎5. 同类二次根式：化简后被开方数相同的二次根式。‎ 知识点7 二次根式的性质 ‎①是一个非负数； ②‎ ‎③ ④‎ ‎⑤‎ 知识点8 二次根式的运算 ‎（1）二次根式的加减 ‎ 二次根式相加减，先把各个二次根式化成最简二次根式，再把同类二次根式分别合并．‎ ‎ （2）二次根式的乘法 ‎ 二次根式相乘，等于各个因式的被开方数的积的算术平方根，即 二次根式的和相乘，可参照多项式的乘法进行．‎ ‎ 两个含有二次根式的代数式相乘，如果它们的积不含有二次根式，那么这两个二次根式互为有理化因式．‎ ‎ （3）二次根式的除法 ‎ ‎ ‎ 二次根式相除，通常先写成分式的形式，然后分子、分母都乘以分母的有理化因式，把分母的根号化去（或分子、分母约分）．把分母的根号化去，叫做分母有理化．‎ 例题精讲 例1. 如果单项式与的和①为0时，a、m、n各为多少？ ②仍为一个单项式，a、m、n各为多少？‎ 解：① ② ‎ a为有理数 ‎ 例2. 因式分解：（1） （2） （3）－2x2＋5xy＋2y2　　‎ 解：①原式＝m（2x＋3y）（2x－3y） ‎ ‎②原式 ‎③令 ‎∴ ∴ ‎ 原式＝－2（x－）（x－）‎ 例3. （1）已知的结果中不含项，求k的值；‎ ‎（2）的一个因式是，求k的值；‎ 解：（1）a2的系数为：3k－2＝0 ∴k＝‎ ‎（2）当a＝－1时（－1）3－（－1）2＋（－1）＋k＝0 ∴k＝3‎ 例4. 利用简便方法计算：（2＋1）（22＋1）（24＋1）（28＋1）（216＋1）（232＋1）的值，‎ 你能确定积的个位数是几吗？‎ 解：（2＋1）（22＋1）（24＋1）（28＋1）（216＋1）（232＋1）‎ ‎＝264－1 ∵264的个位数为6 ∴积的个位数字为5‎ 例5. x为何值时，下列分式的值为0?无意义？‎ ‎（1） （2） ‎ 解：当①x＝2 ②x＝1 时为零 当③x＝－2 ④x＝2，x＝－1时分式无意义 例6. 分式的约分与通分 ‎1. 约分： 2. 通分，，‎ 解：①原式＝ ②,,‎ 例7. 先化简后再求值：，其中 原式＝×＋‎ ‎ ＝＋＝‎ 当x＝＋1时，原式＝1‎ 例8. 若最简二次根式是同类二次根式，求a的值。‎ 解：1＋a＝‎4a2－2＝0, a1＝1 ， a2＝－‎ 例9. 已知:a＝,求值 解：∵a＝ ∴a＝2－＜1 ‎ 原式＝＋1 ＝－（a－1）＋1 ＝－a＋1＋1＝－a＋2‎ 当a＝时，a＝2－, ‎ ‎∴原式＝－2－－2＋＋2＝－2‎ 例10. 把根号外的因式移到根号内： ‎ ‎（1）； （2）； （3）； （4）‎ 解：（1）原式＝ （2）原式＝ （3）原式＝ （4）原式＝‎ 例11. 观察下列各式及其验证过程 ‎2。验证：‎ ‎3。验证：‎ 根据上述两个等式及其验证过程的基本思路，猜想4的变形结果并进行验证。‎ 针对上述各式反映的规律，写出用n（n为任意自然数，且n≥2）表示的等式,并给出证明。‎ 解：（1） ‎ ‎（2）‎ 课后练习 一. 选择题 ‎1. 下列运算正确的是（ ）‎ ‎ A. B. C. D. ‎ ‎2. 把a2－a－6分解因式，正确的是（ ）‎ A. a（a－1）－6 B. （a－2）（a＋3） C. （a＋2）（a－3） D. （a－1）（a＋6）‎ ‎3. 设（x＋y）（x＋2＋y）－15＝0,则x＋y的值是（　　）‎ A. －5或3 B. －3或‎5 ‎ C. 3 D. 5‎ ‎4. 不论ａ为何值，代数式－ａ2＋4ａ－5的值（　　）‎ A. 大于或等于0 B. ‎0 ‎ C. 大于0 D. 小于0‎ ‎5. 化简二次根式的结果是（ ）‎ A. B. C. D. ‎ ‎6. 下列命题：（1）任何数的平方根都有两个（2）如果一个数有立方根，那么它一定有平方根（3）算术平方根一定是正数（4）非负数的立方根不一定是非负数，错误的个数为（ ）‎ A. 1 B. ‎2 ‎ C. 3 D. 4‎ ‎7. 当1