中考数学专题复习 圆压轴八大模型题学生用 8页

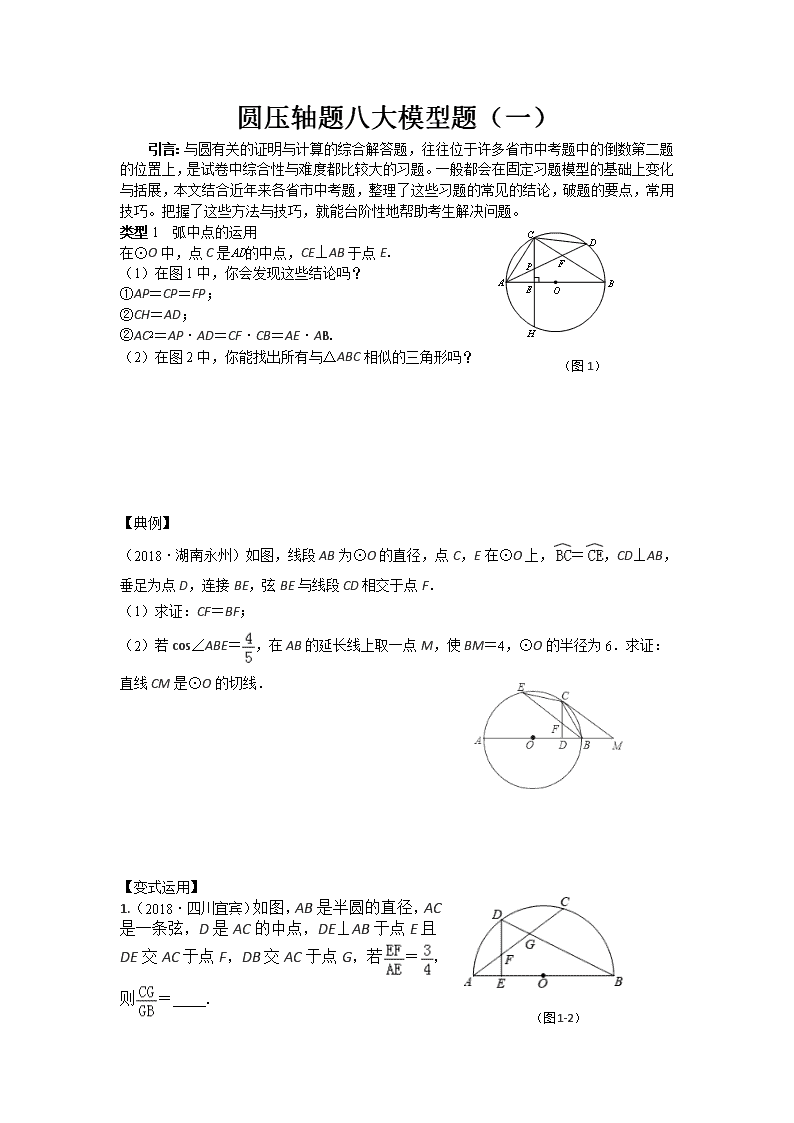
圆压轴题八大模型题（一）‎ ‎ 引言：与圆有关的证明与计算的综合解答题，往往位于许多省市中考题中的倒数第二题的位置上，是试卷中综合性与难度都比较大的习题。一般都会在固定习题模型的基础上变化与括展，本文结合近年来各省市中考题，整理了这些习题的常见的结论，破题的要点，常用技巧。把握了这些方法与技巧，就能台阶性地帮助考生解决问题。‎ 类型1 弧中点的运用 在⊙O中，点C是的中点，CE⊥AB于点E.‎ ‎（1）在图1中，你会发现这些结论吗？‎ ‎①AP＝CP＝FP；‎ ‎②CH＝AD；‎ ‎②AC2＝AP·AD＝CF·CB＝AE·AB.‎ ‎（图1）‎ ‎（2）在图2中，你能找出所有与△ABC相似的三角形吗？‎ ‎【典例】‎ ‎（2018·湖南永州）如图，线段AB为⊙O的直径，点C，E在⊙O上，＝，CD⊥AB，垂足为点D，连接BE，弦BE与线段CD相交于点F．‎ ‎（1）求证：CF＝BF；‎ ‎（2）若cos∠ABE＝，在AB的延长线上取一点M，使BM＝4，⊙O的半径为6．求证：直线CM是⊙O的切线．‎ ‎【变式运用】‎ ‎（图1-2）‎ ‎1.（2018·四川宜宾）如图，AB是半圆的直径，AC是一条弦，D是AC的中点，DE⊥AB于点E且DE交AC于点F，DB交AC于点G，若＝，则＝　　．‎ ‎2.（2018·泸州）如图，在平行四边形ABCD中，E为BC边上的一点，且AE与DE分别平分∠BAD和∠ADC。(1)求证：AE⊥DE；(2)设以AD为直径的半圆交AB于F，连接DF交AE于G，已知CD＝5，AE＝8，求值。‎ ‎（图1-3）‎ ‎3. （2017·泸州）如图，△ABC内接于⊙O，AB是⊙O的直径，C是的中点，弦CE⊥AB于点H，连结AD，分别交CE、BC于点P、Q，连结BD。‎ ‎(1)求证：P是线段AQ的中点；‎ ‎(2)若⊙O的半径为5，AQ＝，求弦CE的长。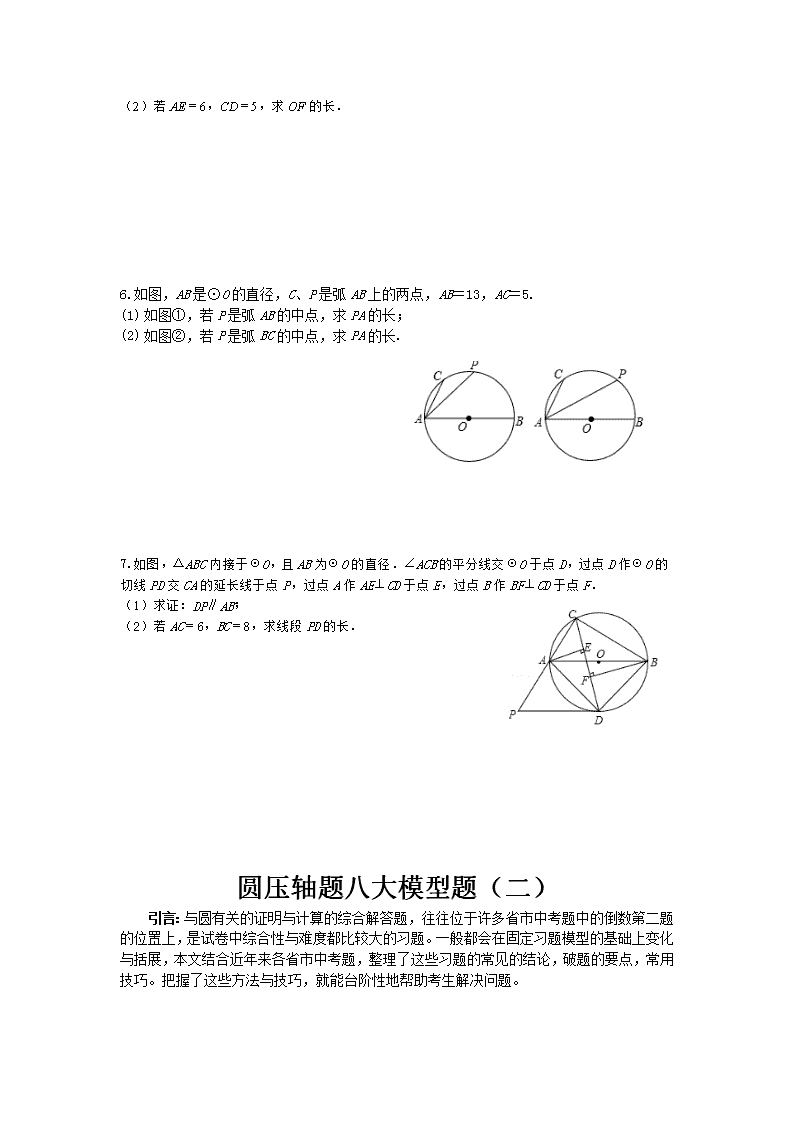‎ ‎4．（2016•泸州）如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AC和BD相交于点E，且DC2＝CE•CA．‎ ‎（1）求证：BC＝CD；‎ ‎（2）分别延长AB，DC交于点P，过点A作AF⊥CD交CD的延长线于点F，若PB＝OB，CD＝，求DF的长．‎ ‎5．（2015•泸州）如图，△ABC内接于⊙O，AB＝AC，BD为⊙O的弦，且AB∥CD，过点A作⊙O的切线AE与DC的延长线交于点E，AD与BC交于点F．‎ ‎（1）求证：四边形ABCE是平行四边形；‎ ‎（2）若AE＝6，CD＝5，求OF的长．‎ ‎6.如图，AB是⊙O的直径，C、P是弧AB上的两点，AB＝13，AC＝5.‎ (1) 如图①，若P是弧AB的中点，求PA的长；‎ (2) 如图②，若P是弧BC的中点，求PA的长.‎ ‎7.如图，△ABC内接于⊙O，且AB为⊙O的直径．∠ACB的平分线交⊙O于点D，过点D作⊙O的切线PD交CA的延长线于点P，过点A作AE⊥CD于点E，过点B作BF⊥CD于点F．‎ ‎（1）求证：DP∥AB；‎ ‎（2）若AC＝6，BC＝8，求线段PD的长．‎ 圆压轴题八大模型题（二）‎ ‎ 引言：与圆有关的证明与计算的综合解答题，往往位于许多省市中考题中的倒数第二题的位置上，是试卷中综合性与难度都比较大的习题。一般都会在固定习题模型的基础上变化与括展，本文结合近年来各省市中考题，整理了这些习题的常见的结论，破题的要点，常用技巧。把握了这些方法与技巧，就能台阶性地帮助考生解决问题。‎ 类型2 切割线互垂 在Rt△ABC中，点E是斜边AB上一点，以EB为直径的⊙O与AC相切于点D，与BC相交于点F.‎ ‎(5)DB2=BC×BE;‎ ‎(6)AD2=AE×AB.‎ 图(3)‎ 图(2)‎ 图(1)‎ ‎(3)AC=32，AE=10，求r.‎ ‎(4)∠ABD=∠CBD.‎ ‎(1)AD=20,AE=10,求r;‎ ‎(2)AB=40,BC=24,求r.‎ ‎【典例】‎ ‎（2018·四川成都）如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A，D的⊙O分别交AB，AC于点E，F，连接OF交AD于点G.‎ ‎（1）求证：BC是⊙O的切线；‎ ‎（2）设AB＝x，AF＝y，试用含x,y的代数式表示线段AD的长；‎ ‎（3）若BE＝8，sinB＝，求DG的长.‎ ‎【变式运用】‎ ‎1.（2018×泸州）如图，已知AB，CD是⊙O的直径，过点C作⊙O的切线交AB的延长线于点P，⊙O的弦DE交AB于点F，且DF＝EF．‎ ‎（1）求证：CO2＝OF•OP；‎ ‎（2）连接EB交CD于点G，过点G作GH⊥AB于点H，若PC＝4，PB＝4，求GH 的长．‎ ‎2.（2018·云南昆明）如图，AB是⊙O的直径，ED切⊙O于点C，AD交⊙O于点F，∠AC平分∠BAD，连接BF．‎ ‎（1）求证：AD⊥ED；‎ ‎（2）若CD＝4，AF＝2，求⊙O的半径．‎ ‎3.（2018·江苏苏州）如图，AB是⊙O的直径，点C在⊙O上，AD垂直于过点C的切线，垂足为D，CE垂直AB，垂足为E．延长DA交⊙O于点F，连接FC，FC与AB相交于点G，连接OC．‎ ‎（1）求证：CD＝CE；‎ ‎（2）若AE＝GE，求证：△CEO是等腰直角三角形．‎ 圆压轴题八大模型题（三）‎ ‎ 引言：与圆有关的证明与计算的综合解答题，往往位于许多省市中考题中的倒数第二题的位置上，是试卷中综合性与难度都比较大的习题。一般都会在固定习题模型的基础上变化与括展，本文结合近年来各省市中考题，整理了这些习题的常见的结论，破题的要点，常用技巧。把握了这些方法与技巧，就能台阶性地帮助考生解决问题。‎ 类型3 双切线组合 径在直角边——直径在直角三角形的直角边上.‎ Rt△PBC中，∠ABC＝90°，Rt△PBC的直角边PB上有一点A，以线段AB为直径的⊙O与斜边相切于点D.‎ 图(1)‎ 图(2)‎ 图(3)‎ ‎(4)PD2＝PA×PB;‎ ‎(5)PB＝8，tana＝，‎ 求PA和AD.‎ ‎(6)求证:OC∥AD（变式）.‎ ‎(7)若AB＝2,BC＝,‎ 求AD、PD、PA的长.‎ ‎(1)PB＝8,BC＝6,求⊙O的半径r.‎ ‎(2)PD＝4,PB＝8,求BC的长.‎ ‎(3)PD＝4,PA＝2,求⊙O的半径r.‎ ‎【典例】‎ ‎（2018·四川乐山）如图，P是⊙O外的一点，PA、PB是⊙O的两条切线，A、B是切点，PO交AB于点F，延长BO交⊙O于点C，交PA的延长交于点Q，连结AC．‎ ‎（1）求证：AC∥PO；‎ ‎（2）设D为PB的中点，QD交AB于点E，若⊙O的半径为3，CQ＝2，求的值．‎ ‎【变式运用】‎ ‎1.（2016 ×青海西宁）如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．‎ ‎（1）求证：CD是⊙O的切线；‎ ‎（2）过点B作⊙O的切线交CD的延长线于点E，BC=6，．求BE的长．（12分）‎ ‎2.（2018·湖北武汉）如图，PA是⊙O的切线，A是切点，AC是直径，AB是弦，连接PB、PC，PC交AB于点E，且PA＝PB.‎ ‎(1) 求证：PB是⊙O的切线.‎ ‎(2) 若∠APC＝3∠BPC，求的值.‎ ‎3.（2017×泸州）如图，⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D，与边BC相交于点F，OA与CD相交于点E，连接FE并延长交AC边于点G．‎ ‎（1）求证：DF∥AO；‎ ‎（2）若AC＝6，AB＝10，求CG的长．‎ 弧题涉及同弧或等弧所对的 ‎