中考专题扇形和圆锥 14页

扇形和和圆锥 ‎1．用一张面积为60π的扇形铁皮，做成一个圆锥容器的侧面（接缝处不计），若这个圆锥的底面半径为5，则这个圆锥的母线长为 。‎ ‎2．已知圆锥的底面半径是3cm，母线长为6cm，则这个圆锥的侧面积为____ ___cm2．（结果保留π）‎ ‎3．如果圆的半径为6,那么60°的圆心角所对的弧长为______.‎ ‎4．已知扇形的半径为，圆心角的度数为，若将此扇形围成一个圆锥，则围成的圆锥的侧面积为 .‎ ‎5．已知圆锥的底面半径是3cm,高是4cm,则这个圆锥的侧面展开图的面积是________ cm2．‎ ‎6．已知圆锥的高为4cm，底面半径为3cm，则此圆锥的侧面积为 cm2.（结果中保留）‎ ‎7．已知圆锥的高是4,母线长为5,则它的侧面积为________（结果保留）‎ ‎8．已知圆锥底面圆的半径为6cm，它的侧面积为60πcm2，则这个圆锥的高是　　cm．‎ ‎9．用一圆心角为120°，半径为6cm的扇形做成一个圆锥的侧面，则这个圆锥的底面半径是_______。‎ ‎10．一条弧所对的圆心角为135°，弧长等于半径为5cm的圆的周长的3倍，则这条弧的半径为 。‎ ‎11．用半径为30cm，圆心角为120°的扇形卷成一个无底的圆锥形筒，则这个圆锥形筒的底面半径为 cm．‎ ‎12．小红要过生日了，为了筹备生日聚会，准备自己动手用纸板制作一个底面半径为9cm，母线长为30cm的圆锥形生日礼帽，则这个圆锥形礼帽的侧面积为　 　cm2．（结果保留π）‎ ‎13．如图，如果从半径为9的圆形纸片剪去圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为 ‎ ‎14．如图所示，一半径为1的圆内切于一个圆心角为60°的扇形，则扇形的周长为　 　．‎ ‎15．如图，在△ABC中，∠A=90°，AB=AC=2，点O是边BC的中点，半圆O与△ABC相切于点D、E，则阴影部分的面积等于 ‎ ‎16．某台钟的时针长为9分米，从上午7时到上午11时该钟时针针尖走过的路程是 分米（结果保留）．‎ ‎17．在Rt△ABC中，∠C=90°，AC=12，BC=5，将△ABC绕边AC所在直线旋转一周得到圆锥，则该圆锥的侧面积是______.‎ ‎18．如图，现有一圆心角为90°，半径为8cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计），求该圆锥的侧面积和圆锥的高．（结果保留π）‎ ‎19．一个圆锥形零件的母线长为6，底面的半径为2，求这个圆锥形零件的侧面积和全面积．‎ ‎20．如图，一个圆锥的高为,侧面展开图是半圆，求：‎ ‎（1）圆锥的底面半径与母线之比；‎ ‎（2）圆锥的全面积．‎ ‎21．如图,粮仓的顶部是圆锥形,这个圆锥的底面周长为32cm,母线长为7cm,为了防雨,需要在它的顶部铺上油毡,所需油毡的面积至少是多少?‎ ‎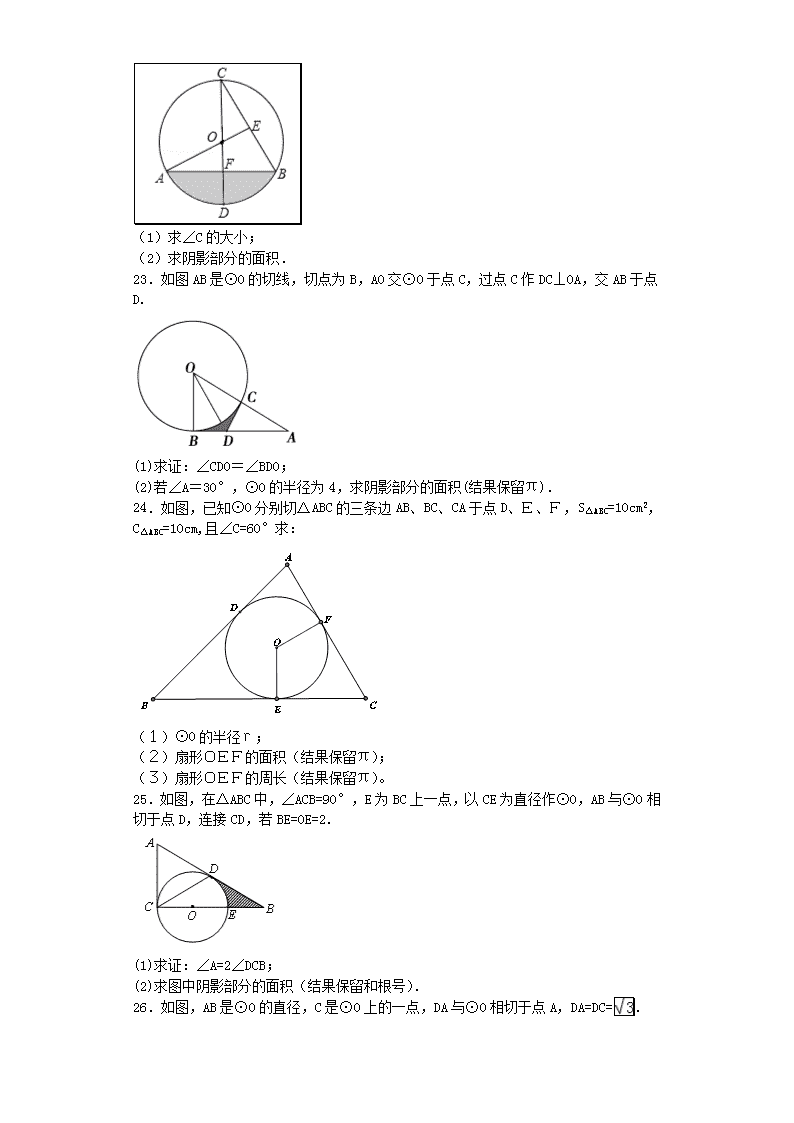22．如图，CD为⊙O的直径，CD⊥AB，垂足为点F，AO⊥BC，垂足为点E，AO=1．‎ ‎（1）求∠C的大小；‎ ‎（2）求阴影部分的面积．‎ ‎23．如图AB是⊙O的切线，切点为B，AO交⊙O于点C，过点C作DC⊥OA，交AB于点D.‎ ‎(1)求证：∠CDO＝∠BDO；‎ ‎(2)若∠A＝30°，⊙O的半径为4，求阴影部分的面积(结果保留π)．‎ ‎24．如图，已知⊙O分别切△ABC的三条边AB、BC、CA于点D、Ｅ、Ｆ，S△ABC=10cm2，C△ABC=10cm,且∠C=60°求：‎ ‎（１）⊙O的半径ｒ；‎ ‎（２）扇形ＯＥＦ的面积（结果保留π）；‎ ‎（３）扇形ＯＥＦ的周长（结果保留π）。‎ ‎25．如图，在△ABC中，∠ACB=90°，E为BC上一点，以CE为直径作⊙O，AB与⊙O相切于点D，连接CD，若BE=OE=2．‎ ‎(1)求证：∠A=2∠DCB；‎ ‎(2)求图中阴影部分的面积（结果保留和根号）．‎ ‎26．如图，AB是⊙O的直径，C是⊙O上的一点，DA与⊙O相切于点A，DA=DC=．‎ ‎（1）求证：DC是⊙O的切线；‎ ‎（2）若∠CAB=30°，求阴影部分的面积．‎ 参考答案 ‎1．12．‎ ‎【解析】‎ 试题分析：先根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长得到扇形的弧长=10π，再根据扇形的半径等于圆锥的母线长和扇形的面积公式求解：‎ 这个圆锥的母线长为l，‎ ‎∵这个圆锥的底面半径为5，∴扇形的弧长=2π•5=10π.‎ ‎∵扇形的面积为60π，∴60π=l•10π，∴l=12．‎ 考点：圆锥的计算．‎ ‎2．18π．‎ ‎【解析】‎ 试题分析：底面圆的半径为3，则底面周长=6π，侧面面积=×6π×6=18πcm2．‎ 故答案是18π．‎ 考点：圆锥的计算．‎ ‎3．‎ ‎【解析】‎ 试题分析：直接根据弧长公式进行计算．‎ 试题解析：根据弧长的公式 考点: 弧长的计算．‎ ‎4．．‎ ‎【解析】‎ 试题分析：圆锥的侧面积=．‎ 故答案是．‎ 考点：圆锥的计算．‎ ‎5．15π．‎ ‎【解析】‎ 试题分析：因为圆锥的底面半径是3,高是4,所以圆锥的母线长为5,所以这个圆锥的侧面展开图的面积是π×3×5=15π．‎ 故答案是15π．‎ 考点：圆锥的计算．‎ ‎6．15π.‎ ‎【解析】‎ 试题分析：∵高线长为4cm，底面的半径是3cm，∴由勾股定理知：母线长为5cm.‎ ‎∴圆锥侧面积=底面周长×母线长=×6π×5=15π(cm2)．‎ 考点：1.勾股定理;2.圆锥的计算．‎ ‎7．15π．‎ ‎【解析】‎ 试题分析：圆锥的高是4,母线长为5,所以圆锥的底面半径是3.圆锥的侧面积=2π×3×5÷2=15π．‎ 故答案是15π．‎ 考点：圆锥的计算．‎ ‎8．8.‎ ‎【解析】‎ 试题分析：设圆锥的母线长为l，由于圆锥的侧面展开图为扇形，扇形的弧长等于圆锥底面圆的周长，扇形的半径等于圆锥的母线长，则l•2π•6=60π，然后利用勾股定理计算圆锥的高．‎ 试题解析：设圆锥的母线长为l，‎ 根据题意得 ‎ l•2π•6=60π，‎ 解得l=10，‎ 所以圆锥的高=（cm）．‎ 考点: 圆锥的计算.‎ ‎9．2cm．‎ ‎【解析】‎ 试题分析：利用圆锥的侧面展开图中扇形的弧长等于圆锥底面的周长可得．‎ 试题解析：设此圆锥的底面半径为r，由题意，得 ‎，‎ 解得r=2cm．‎ 考点: 圆锥的计算．‎ ‎10．40cm.‎ ‎【解析】‎ 试题分析：设出弧所在圆的半径，由于弧长等于半径为5cm的圆的周长的3倍，所以根据原题所给出的等量关系，列出方程，解方程即可．‎ 试题解析：设弧所在圆的半径为r，‎ 由题意得， ‎ ‎，‎ 解得，r=40cm．‎ 考点:圆心角、弧、弦的关系.‎ ‎11．10．‎ ‎【解析】‎ 试题分析：扇形的弧长是：=20πcm，‎ 设底面半径是r，则2πr=20π，‎ 解得：r=10．‎ 故答案是10．‎ 考点：圆锥的计算．‎ ‎12．270π．‎ ‎【解析】‎ 试题分析：圆锥的侧面积=π×底面半径×母线长，把相关数值代入计算即可．‎ 试题解析：圆锥形礼帽的侧面积=π×9×30=270πcm2．‎ 考点: 圆锥的计算.‎ ‎13．.‎ ‎【解析】‎ 试题分析：因为圆锥的高，底面半径，母线构成直角三角形，则留下的扇形的弧长=，所以圆锥的底面半径r=12π÷2π=6，所以圆锥的高=. ‎ 试题解析：∵从半径为9cm的圆形纸片剪去圆周的一个扇形，‎ ‎∴剩下的扇形的角度=360°×=240°，‎ ‎∴留下的扇形的弧长=，‎ ‎∴圆锥的底面半径r=12π÷2π=6，‎ ‎∴圆锥的高=.‎ 考点: 1.弧长的计算；2.勾股定理．‎ ‎14．6+．‎ ‎【解析】‎ 试题分析：首先求出扇形半径，进而利用扇形弧长公式求出扇形弧长，进而得出扇形周长．‎ 试题解析：如图所示：设⊙O与扇形相切于点A，B，‎ 则∠CAO=90°，∠ACB=30°，‎ ‎∵一半径为1的圆内切于一个圆心角为60°的扇形 ‎∴AO=1，‎ ‎∴CO=2AO=2，‎ ‎∴BC=2+1=3，‎ ‎∴扇形的弧长为：‎ ‎∴则扇形的周长为：3+3+=6+．‎ 考点: 1.相切两圆的性质；2.弧长的计算.‎ ‎15．．‎ ‎【解析】‎ 试题分析：首先连接OD，OE，易得△BDF≌△EOF，继而可得S阴影=S扇形DOE，即可求得答案．‎ 试题解析：连接OD，OE，‎ ‎∵半圆O与△ABC相切于点D、E，‎ ‎∴OD⊥AB，OE⊥AC，、‎ ‎∵在△ABC中，∠A=90°，AB=AC=2，‎ ‎∴四边形ADOE是正方形，△OBD和△OCE是等腰直角三角形，‎ ‎∴OD=OE=AD=BD=AE=EC=1，‎ ‎∴∠ABC=∠EOC=45°，‎ ‎∴AB∥OE，‎ ‎∴∠DBF=∠OEF，‎ 在△BDF和△EOF中，‎ ‎，‎ ‎∴△BDF≌△EOF（AAS），‎ ‎∴．‎ 考点: 1.切线的性质；2.扇形面积的计算．‎ ‎16．6π．‎ ‎【解析】‎ 试题分析：从上午7时到上午11时，时针共转了4个大格共120°，然后根据弧长公式算出时针针尖走过的路程．‎ 试题解析：∵时针从上午7时走到上午11时 ‎∴时针共转了120°‎ ‎∴时针尖走过的路程为：（分米）．‎ 故答案为：6π．‎ 考点: 1.弧长的计算；2.钟面角．‎ ‎17．‎ ‎【解析】由已知得，圆锥的母线长，底面半径为5，∴ 圆锥的侧面积是．‎ ‎18．圆锥的高为cm，侧面积为16πcm2．‎ ‎【解析】‎ 试题分析：利用扇形的弧长公式可得圆锥侧面展开图的弧长，除以2π即为圆锥的底面半径，利用勾股定理可得圆锥的高，圆锥的侧面积=π×底面半径×母线长，把相关数值代入计算即可．‎ 试题解析：：∵扇形的弧长为cm， ∴圆锥底面的周长为4πcm， ∴圆锥底面的半径为4π÷（2π）=2cm， ∴圆锥底面的高为（cm） 圆锥的侧面积=π×2×8=16π（cm2）， 答：圆锥的高为cm，侧面积为16πcm2．‎ 考点: 1.圆锥的计算；2.扇形面积的计算.‎ ‎19．见解析.‎ ‎【解析】‎ 试题分析：圆锥形的侧面积为底面周长乘以高,关键求高,根据勾股定理可得高 ‎,全面积等于侧面积加上一个圆的面积.‎ 试题解析：根据勾股定理可得高 ‎,.‎ 考点：1.圆锥形的侧面积和全面积.2.勾股定理.‎ ‎20．详见解析 ‎【解析】‎ 试题分析：‎ ‎（1）由题意可知：圆锥的底面周长等于圆锥的弧长，由此可得，化简可得：. （2）首先根据勾股定理可求得圆锥的底面半径和圆锥的母线的长度，然后利用圆锥的侧面积即展开图的半圆面积加上圆锥的底面积即可求出圆锥的全面积.‎ 试题解析：‎ 解：（1）由题意可知 ‎∴，‎ ‎∴‎ ‎（2）在中，‎ ‎∵‎ ‎∴‎ ‎∴‎ ‎∴‎ ‎∴‎ ‎∵‎ ‎∴，‎ ‎∴‎ ‎∴‎ 考点：圆锥的全面积的计算.‎ ‎21．112cm2.‎ ‎【解析】‎ 试题分析：圆锥的侧面积S=LR==,其中R是扇形母线,L是扇形弧长,也是底面圆周的周长,由题, 这个圆锥的底面周长为32cm,母线长为7cm,所以L=32cm,R=7cm,所以112 cm2 .‎ 试题解析：∵圆锥的底面周长为32cm,母线长为7cm,‎ ‎∴ 圆锥的侧面积为：112cm2 ,‎ 答：所需油毡的面积至少是112cm2.‎ 考点：圆锥的侧面积.‎ ‎22．解：（1）∵CD是圆O的直径，CD⊥AB，∴。∴∠C=∠AOD。‎ ‎∵∠AOD=∠COE，∴∠C=∠COE。‎ ‎∵AO⊥BC，∴∠C=30°。‎ ‎（2）连接OB，‎ 由（1）知，∠C=30°，∴∠AOD=60°。∴∠AOB=120°。‎ 在Rt△AOF中，AO=1，∠AOF=60°，∴AF=，OF=。‎ ‎∴AB=。‎ ‎∴。‎ ‎【解析】‎ 试题分析：（1）根据垂径定理可得，∠C=∠AOD，然后在Rt△COE中可求出∠C的度数。‎ ‎（2）连接OB，根据（1）可求出∠AOB=120°，在Rt△AOF中，求出AF，OF，然后根据S阴影=S扇形OAB﹣S△OAB，即可得出答案。　‎ ‎23．（1）见解析 （2）－‎ ‎【解析】‎ ‎(1)证明：AB切⊙O于点B，‎ ‎∴OB⊥AB，即∠B＝90°.‎ 又∴DC⊥OA，∴∠OCD＝90°.‎ 在Rt△COD与Rt△BOD中，OD＝OD，OB＝OC，‎ ‎∴Rt△COD≌Rt△BOD.‎ ‎∴∠CDO＝∠BDO.‎ ‎(2)在Rt△ABO中，∠A＝30°，OB＝4，‎ ‎∴∠BOC＝60°，‎ ‎∵Rt△COD≌Rt△BOD，‎ ‎∴∠BOD＝30°，‎ ‎∴BD＝OB·tan 30°＝.‎ ‎∴S四边形OCDB＝2S△OBD＝2××4×＝.‎ ‎∵∠BOC＝60°，‎ ‎∴S扇形OBC＝＝.‎ ‎∴S阴影＝S四边形OCDB－S扇形OBC＝－.‎ ‎24．（1）2cm；(2) cm2；（3）（cm）.‎ ‎【解析】‎ 试题分析：（1）连接AO、BO、CO，根据S△ABC=S△AOC+S△AOB+S△BOC即可求出⊙O的半径；‎ ‎（2）因为OF⊥AC，OE⊥BC，∠C=60°可求出∠EOF的度数，代入扇形面积计算公式即可求出扇形的面积；‎ ‎（3）利用扇形的周长=扇形的弧长+半径×2，即可求出扇形的周长.‎ 试题解析:(1)如图，连接AO、BO、CO，‎ 则S△ABC=S△AOC+S△AOB+S△BOC ‎，‎ 又AB+BC+AC=10，‎ ‎∴r=2cm；‎ ‎（2）因为OF⊥AC，OE⊥BC，∠C=60°‎ 所以∠EOF=120°‎ 所以S扇形EOF= cm2‎ ‎（3）扇形EOF的周长=（cm）.‎ 考点: 1.面积法；2.扇形面积计算；3.扇形弧长计算.‎ ‎25．（1）证明见解析；（2）.‎ ‎【解析】‎ 试题分析：（1）连接OD，则OD⊥AB，可知∠A=∠DOB.由∠DOB=2∠DCB得：∠A=2∠DCB；‎ ‎（2）由图形可知：阴影部分的面积=S△BOD-扇形DOE的面积，代入相关数据即可求出.‎ 试题解析：（1）证明：连接OD．‎ ‎∵AB与⊙O相切于点D，‎ ‎∴ OD⊥AB，‎ ‎∴∠B＋∠DOB=90°．‎ ‎∵∠ACB=90°，‎ ‎∴∠A＋∠B=90°，‎ ‎∴∠A=∠DOB．‎ ‎∵OC=OD，‎ ‎∴∠DOB=2∠DCB．‎ ‎∴∠A=2∠DCB．‎ ‎（2）在Rt△ODB中，‎ ‎∵OD=OE，OE=BE，‎ ‎∴sin∠B=，‎ ‎∴∠B=30°，∠DOB=60°．‎ ‎∵BD=OB·sin60°=，‎ ‎∴， ‎ ‎∴.‎ 考点: 1.切线的判定；2.扇形面积的计算.‎ ‎26．（1）证明见解析；（2）.‎ ‎【解析】‎ 试题分析：（1）连接OC，证明OC⊥DC，即可得到DC是⊙O的切线；‎ ‎（2）根据阴影部分的面积=扇形的面积-△BOC的面积计算即可．‎ 试题解析：（1）证明：连接OC，‎ ‎∵DA=DC，‎ ‎∴∠DAC=∠DCA，‎ ‎∵DA与⊙O相切于点A，‎ ‎∴∠DAB=90°，‎ ‎∴∠DAC+∠CAB=90°，‎ ‎∵OC=OA，‎ ‎∴∠OAC=∠OCA，‎ ‎∴∠DCA+∠ACO=90°，‎ 即OC⊥DC，‎ ‎∴DC是⊙O的切线；‎ ‎（2）∵阴影部分的面积=扇形的面积-△BOC的面积，‎ ‎∴阴影部分的面积=．‎ 考点:1.切线的判定与性质；2.扇形面积的计算．单纯的课本内容，并不能满足学生的需要，通过补充，达到内容的完善 ‎ 教育之通病是教用脑的人不用手，不教用手的人用脑，所以一无所能。教育革命的对策是手脑联盟，结果是手与脑的力量都可以大到不可思议。‎