中考数学能力测试卷 4页

‎2004年中考数学模拟测试卷 卷一 说明：本卷有1大题，12个小题，共48分．解答时应在答题卡上用铅笔把所选项对应字母的括号涂黑、涂满．‎ 一、选择题（本题有12题，每小题4分，共48分．请选出各题中一个符合题意的正确选项，不选、多选、错选均分给分）‎ ‎1．-7的绝对值是（ ）‎ A．-7 B．7 C． D．‎ ‎2．下列式子中正确的是（ ）‎ A． B． C． D．‎ ‎3．如图，∠1=∠2，则下列结论一定成立的是（ ）‎ A．AB∥CD B．AD∥BC C．∠B=∠D D．∠3=∠4‎ ‎4．9的算术平方根是（ ）‎ A．3 B．±3 C． D．‎ ‎5．一个角的余角是40°，这个角是（ ）‎ A．40° B．50° C．140° D．60°‎ ‎6．抛物线的顶点坐标是（ ）‎ A．（1，5） B．（-1，-5） C．（-1，-4） D．（-2，-7）‎ ‎7．两圆的半径分别是3㎝和4㎝，圆心距为1㎝，则两圆的位置关系是（ ）‎ A．内切 B．外切 C．相交 D．外离 ‎8．对实数满足，则实数在数轴上的对应点在（ ）‎ A．原点右侧 B．原点左侧 C．原点或其右侧 D．原点或其左侧 ‎9．使分式的值为正的取值范围是（ ）‎ A． B．且 C．且 D．‎ ‎10．等腰三角形底边上的高线长等于腰长的一半，则顶角为（ ）‎ A．30° B．60° C．90° D．120°‎ ‎11．若，则等于（ ）‎ A． B． C． D．‎ ‎12．如果某一年的七月份有5天是星期一，那么这一年的8月份一定有5天是（ ）‎ A．星期二 B．星期三 C．星期四 D．星期五 卷二 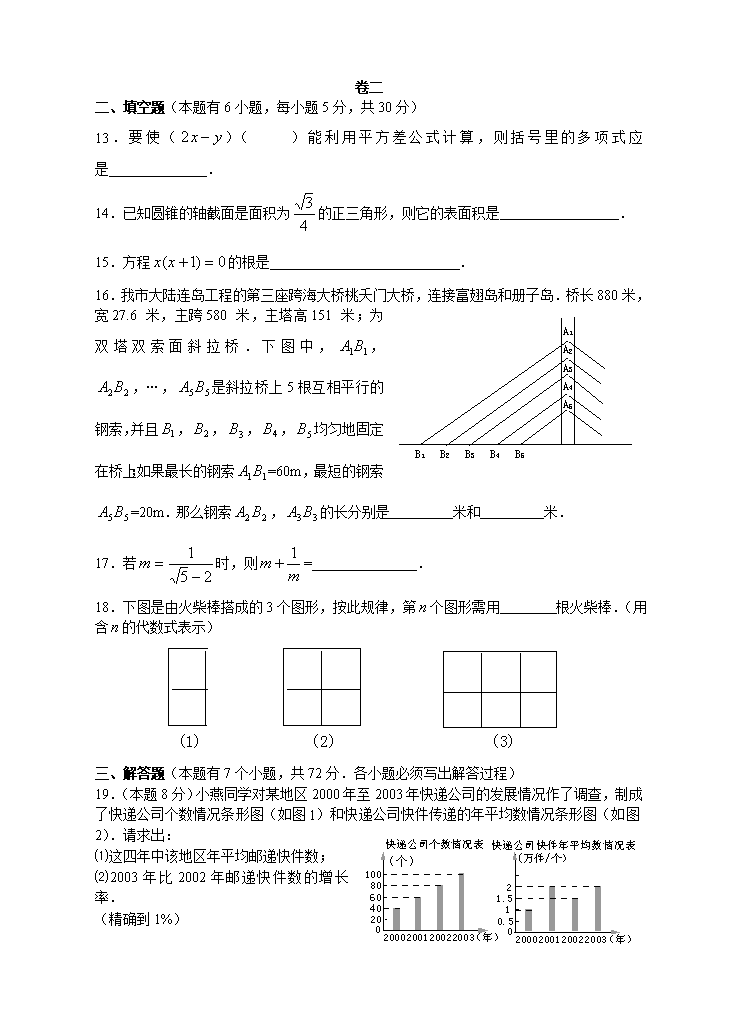二、填空题（本题有6小题，每小题5分，共30分）‎ ‎13．要使（）（ ）能利用平方差公式计算，则括号里的多项式应是 ．‎ ‎14．已知圆锥的轴截面是面积为的正三角形，则它的表面积是 ．‎ ‎15．方程的根是 ．‎ ‎16．我市大陆连岛工程的第三座跨海大桥桃夭门大桥，连接富翅岛和册子岛．桥长880米，宽27.6米，主跨580米，主塔高151米；为双塔双索面斜拉桥．下图中，，，…，是斜拉桥上5根互相平行的钢索，并且，，，，均匀地固定在桥上；如果最长的钢索=60m，最短的钢索=20m．那么钢索，的长分别是 米和 米．‎ ‎17．若时，则= ．‎ ‎18．下图是由火柴棒搭成的3个图形，按此规律，第个图形需用 根火柴棒．（用含的代数式表示）‎ ‎ ‎ 三、解答题（本题有7个小题，共72分．各小题必须写出解答过程）‎ ‎19．（本题8分）小燕同学对某地区2000年至2003年快递公司的发展情况作了调查，制成了快递公司个数情况条形图（如图1）和快递公司快件传递的年平均数情况条形图（如图2）．请求出：‎ ‎（个）‎ ‎⑴这四年中该地区年平均邮递快件数；‎ ‎⑵2003年比2002年邮递快件数的增长率．‎ ‎（精确到1%）‎ ‎20．（本题8分）一家商店将某种型号的彩电先按原价提高40%，然后再以“大酬宾，八折销售”卖给消费者．经消费者投诉，执法部门按已得非法收入的10倍金额予以每台2700元的罚款，求每台彩电的原价是多少？‎ ‎21．（本题8分）如图，已知正方形ABCD中，E是BC的中点，F在CD上，且DF=3CF．‎ 求证：△ABE∽△ECF．‎ ‎22. （本题10分）如图，小强在江南岸选定建筑物A，并在江北岸的B处观察．此时视线与江岸BE所成的夹角为30°；小强沿江岸BE向东走了500米到C处，再观察A．此时视线AC与江岸所成的夹角∠ACE=60°．根据小强提供的信息，你能测出江宽吗？若能，写出求解过程；若不能，请说明理由．‎ ‎23．（本题12分）研究发现：某种感冒药有使人感到困倦的物质．右图是成年人服用感冒药后，使人感到困倦的物质在人体每毫升血液中的含量（微克）随服药时间（时）变化的关系图．‎ ‎（1）求出与的函数关系式；‎ ‎（2）如果当每毫升血液中该物质的含量不少于4微克时，人会有困倦感，求：服药这种药后人会感到困倦的时间．‎ ‎24．（本题12分）已知关于的二次函数的图象与轴的两个交点A（，0），B（，0）．（1）若，求的取值范围；（2）问：A，B两点是否都能在轴的正半轴上？若能，求出相应的的取值范围；若不能，请说明理由．‎ ‎25．（本题14分）已知是正方形ABCD对角线AC上的一点，以O为圆心，OA的长为半径的⊙O与BC相切于M，与AB分别相交于E，F．‎ ‎（1）求证：CD与⊙O相切；‎ ‎（2）若正方形ABCD的边长为1，求⊙O的半径；‎ ‎ （3）对于以点M，E，A，F以及CD与⊙O的切点为顶点的五边形的五条边，从相等的关系考虑，你可以得出什么结论？请给出证明．‎