- 537.22 KB
- 2021-05-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2011年凉山州高中阶段招生统一考试
数学试卷
本试卷共10页,分为A卷(120分)、B卷(30分),全卷150分,考试时间120分钟。A卷又分为第Ι卷和第II卷。
注意事项
1. 第 卷答在题卡上,不能答在试卷上,答卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2. 每小题选出答案后,用2B或3B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案。
A卷(共120分)
第I卷(选择题 共48分)
注意事项:
1.第I卷答在答题卡上,不能答在试卷上。答卷前,考生务必将自己的姓名、准考证号、试题科目涂写在答题卡上。
2.每小题选出答案后,用2B或3B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案。
一、选择题(共12个小题,每小题4分,共48分)在每小题给出的四个选项中只有一项是正确的,把正确的字母填涂在答题卡上相应的位置。
1. 的倒数是( )
A. B. C.2 D.
2. 下列不等式变形正确的是( )
A.由,得 B.由,得
C.由,得 D.由,得
3. 下列方程组中是二元一次方程组的是( )
A. B. C. D.
4. 下列说法正确的是( )
A.随机抛掷一枚均匀的硬币,落地后反面一定朝上。
B.从1,2,3,4,5中随机取一个数,取得奇数的可能性较大。
C.某彩票中奖率为,说明买100张彩票,有36张中奖。
D.打开电视,中央一套正在播放新闻联播。
5. 已知,则的值为( )
A. B. C. D.
6. 某品牌服装原价173元,连续两次降价后售价价为127元,下面所列方程中正确的是( )
A. B.
C. D.
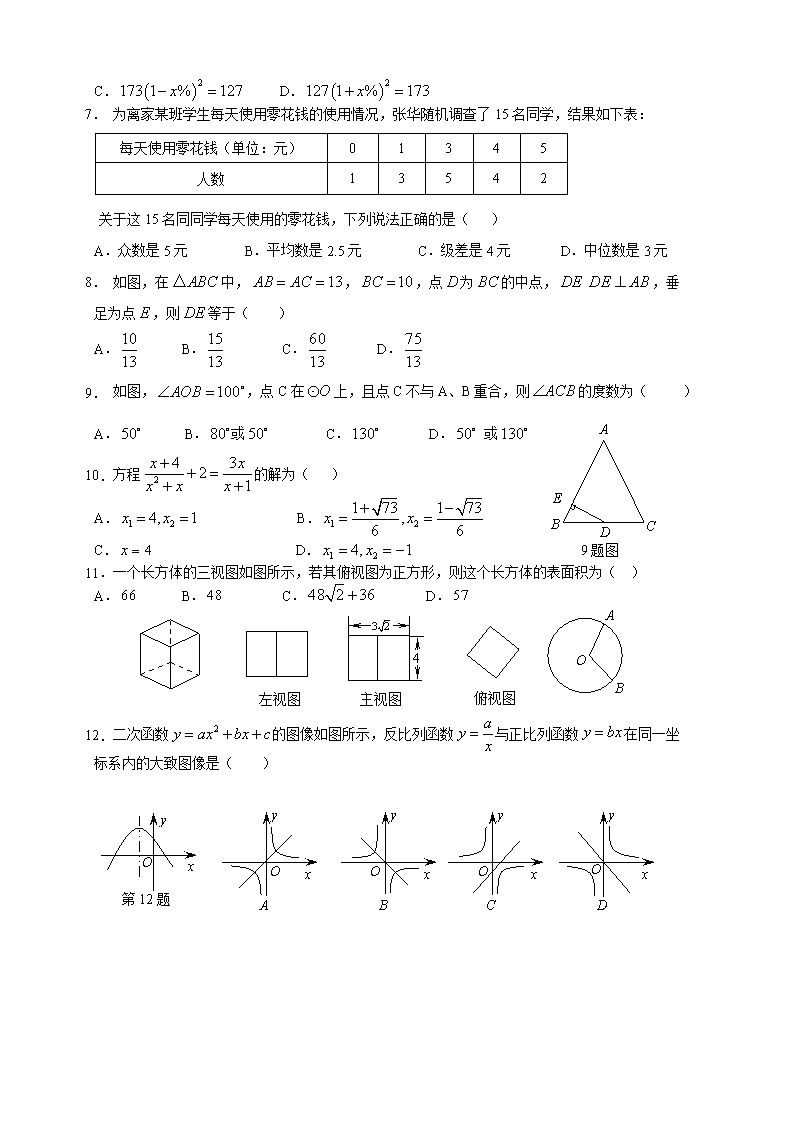
1. 为离家某班学生每天使用零花钱的使用情况,张华随机调查了15名同学,结果如下表:
每天使用零花钱(单位:元)
0
1
3
4
5
人数
1
3
5
4
2
关于这15名同同学每天使用的零花钱,下列说法正确的是( )
A.众数是5元 B.平均数是2.5元 C.级差是4元 D.中位数是3元
2. 如图,在中,,,点为的中点,,垂足为点,则等于( )
A. B. C. D.
3. 如图,,点C在上,且点C不与A、B重合,则的度数为( )
E
D
C
A
B
9题图
A. B.或 C. D. 或
4. 方程的解为( )
A. B.
C. D.
5. 一个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的表面积为( )
A. B. C. D.
左视图
主视图
4
俯视图
A
B
O
6. 二次函数的图像如图所示,反比列函数与正比列函数在同一坐标系内的大致图像是( )
O
y
x
B
第12题
O
x
y
O
y
x
A
O
y
x
D
O
y
x
C
县(市): 区(乡 镇) 校,姓名 准考证号
··○····○··密····○····封····○····线····○····内····○····不····○····能····○····答····○····题····○····○··
2011年凉山州高中阶段招生统一考试
数 学 试 卷
题号
A卷
B卷
总分人
二
三
四
五
总分
六
七
总分
得分
第II卷(非选择题 共72分)
注意事项:
1.答卷前将密封线内的项目填写清楚,准考证号前7位填在密封线方框内,末两位填在句首方框内。
2.答题时用钢笔或圆珠笔直接答在试卷上。
得分
评卷人
二、填空题(共5小题,每小题4分,共20分)
1. 用科学计数法表示0.0000023 = 。
2. 分解因式: 。
3. 把命题“如果直角三角形的两直角边长分别为a、b,斜边长为c,那么”的逆命题改写成“如果……,那么……”的形式:
。
第16题图
4. 如图,有三个同心圆,由里向外的半径依次是2cm,4cm, 6cm将圆盘分为三部分,飞镖可以落在任何一部分内,那么飞镖落在阴影圆环内的概率是 。
5. 已知菱形ABCD的边长是8,点E在直线AD上,若DE=3,连接BE与对角线AC相交于点M,则的值是 。
得分
评卷人
三、解答题(共2小题,每小题6分,共12分)
1. 计算:
2. 我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例。如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律。例如,在三角形中第三行的三个数1,2,1,恰好对应展开式中的系数;第四行的四个数1,3,3,1,恰好对应着展开式中的系数等等。
1
1
1
2
1
1
3
3
1
1
…………………………(a+b)1
…………………………(a+b)2
…………………………(a+b)3
……………………
(1)根据上面的规律,写出的展开式。
(2)利用上面的规律计算:
得分
评卷人
四、解答题( 共3小题,20题7分,21题、22题各8分,共23分)
B
C
D
E
F
A
20题图
1. 如图,是平行四边形的对角线上的点,,请你猜想:线段与线段有怎样的关系?并对你的猜想加以证明。
2. 在平面直角坐标系中,已知三个顶点的坐标分别为
(1)画出,并求出所在直线的解析式。
(2)画出绕点顺时针旋转后得到的,并求出在上述旋转过程中1
1
Ox
y
x
21题图
扫过的面积。
1. 6张不透明的卡片,除正面画有不同的图形外,其它均相同,把这6张卡片洗匀后,正面向下放在桌上,另外还有与卡片上图形形状完全相同的地板砖若干块,所有地板砖的长都相等。
⑴从这6张卡片中随机抽取一张,与卡片上图形形状相对应的这种地板砖能进行平面镶嵌的概率是多少?
⑵从这6张卡片中随机抽取2张,利用列表或画树状图计算:与卡片上图形形状相对应的这两种地板砖能进行平面镶嵌的概率是多少?
正三角形
A
正方形
B
D
正六边形
正五边形
C
E
正八边形
正十边形
F
得分
评卷人
五、解答题(共2小题,23题8分,24题9分,共17分)
1. 在一次课题设计活动中,小明对修建一座87m长的水库大坝提出了以下方案;大坝的横截面为等腰梯形,如图,∥,坝高10m,迎水坡面的坡度,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面的坡度进行修改,修改后的迎水坡面的坡度。
(1) 求原方案中此大坝迎水坡的长(结果保留根号)
A
B
C
E
D
23题图
(2) 如果方案修改前后,修建大坝所需土石方总体积不变,在方案修改后,若坝顶沿方向拓宽2.7m,求坝顶将会沿方向加宽多少米?
1. 我州鼓苦荞茶、青花椒、野生蘑菇,为了让这些珍宝走出大山,走向世界,州政府决定组织21辆汽车装运这三种土特产共120吨,参加全国农产品博览会。现有A型、B型、C型三种汽车可供选择。已知每种型号汽车可同时装运2种土特产,且每辆车必须装满。根据下表信息,解答问题。
特产
车型
苦荞茶
青花椒
野生蘑菇
每
辆
汽
车
运
载
量
(吨)
A型
2
2
B型
4
2
C型
1
6
车型
A
B
C
每辆车运费(元)
1500
1800
2000
(1) 设A型汽车安排辆,B 型汽车安排辆,求与之间的函数关系式。
(2) 如果三种型号的汽车都不少于4辆,车辆安排有几种方案?并写出每种方案。
(3) 为节约运费,应采用(2)中哪种方案?并求出最少运费。
B卷(共30分)
得分
评卷人
六、填空题(共2小题,每小题5分,共10分)
B
A
第26题图
1. 已知为有理数,分别表示的整数部分和小数部分,且,则 。
2. 如图,圆柱底面半径为,高为,点分别是圆柱两底面圆周上的点,且、在同一母线上,用一棉线从顺着圆柱侧面绕3圈到,求棉线最短为 。
得分
评卷人
七、解答题(共2小题,27题8分,28题12分,共20分)
3. 如图,已知,以为直径,为圆心的半圆交于点,点为的中点,连接交于点,为的角平分线,且,垂足为点。
(1) 求证:是半圆的切线;
B
D
O
H
C
E
M
F
A
27题图
(2) 若,,求的长。
1. 如图,抛物线与轴交于(,0)、(,0)两点,且,与轴交于点,其中是方程的两个根。
(1)求抛物线的解析式;
(2)点是线段上的一个动点,过点作∥,交于点,连接,当的面积最大时,求点的坐标;
(3)点在(1)中抛物线上,点为抛物线上一动点,在轴上是否存在点,使以为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点的坐标,若不存在,请说明理由。
y
x
O
B
M
N
C
A
28题图
2011年凉山州高中阶段招生统一考试
数学参考答案及评分意见
A卷(共120分)
一、选择题(共12小题,每小题4分,共48分)
1.A 2.B 3.D 4.B 5.A 6.C 7.D 8.C 9.D 10.C 11.A 12.B
二、填空题(共5小题,每小题4分,共20分)
13. 14. 15.如果三角形三边长a,b,c,满足,那么这个三角形是直角三角形 16. 17.或
三、解答题(共2小题,每小题6分,共12分)
18.解:原式=································2分
=················································4分
=························································6分
19.解:(1)·····················3分
(2)原式=····5分
=
=1 。······················································6分
注:不用以上规律计算不给分.
四、解答题(共3小题,20小题7分,21题、22题各8分,共23分)
20.猜想:。
证明: ∵四边形ABCD是平行四边形 ,·················2分
A
B
C
O
B1
C1
A1
x
y
1
1
∴,∥。
∴ 。
在和,
∴≌。 ···········5分
∴,,
∴∥。
即 。·····················7分
21.(1)如图所示,即为所求。·····1分
设所在直线的解析式为
∵,
∴ 解得 , ∴。 ················3分
(2)如图所示,即为所求 ···4分
由图可知, ·········5分
·············6分
··············8分
22.解:(1)··················································3分
(2)根据题意得:
A
B
C
D
E
F
A
AB
AC
AD
AE
AF
B
BA
BC
BD
BE
BF
C
CA
CB
CD
CE
························5分
CF
D
DA
DB
DC
DE
DE
F
EA
EB
EC
ED
EF
FA
FB
FC
FD
FE
由上表可知,共有30种可能的结果,且每种结果的可能性相同,其中能进行平面镶嵌的结果有8种,分别是:AB, AD, BE, CF, BA, DA, EB, FC 。 ·················7分
····················································8分
五、解答题(共2小题,23题8分,24题9分,共17分)
23.解:(1)过点作于。 ·······································1分
在中,∵,且。
∴, ·····································3分
(2)过点作于。
在中,∵,且。,
∴,。 ························5分
A
B
C
M
D
G
F
E
N
如图,延长至点,至点,
连接,
∵方案修改前后,修建大坝所需土石方
总体积不变。
∴ ············7分
。
即 。
。
答:坝底将会沿方向加宽。 ·······························8分
24.解:(1) 法① 根据题意得
····································2分
化简得: 。 ··········································3分
法② 根据题意得
化简得:。 ··········································3分
(2)由 得
解得 。 ·············································5分
∵为正整数,∴,6,7。 ······································6
分
故车辆安排有三种方案,即:
方案一:型车辆,型车辆,型车辆
方案二:型车辆,型车辆,型车辆
方案三:型车辆,型车辆,型车辆 ·····················6分
(3)设总运费为元,则
。 ·····························8分
∵随的增大而增大,且
∴当时,元。
答:为节约运费,应采用 ⑵中方案一,最少运费为37100元。 ···········9分
B卷(共30分)
六、填空题(共2小题,每小题5分,共10分)
25. 26.
七、解答题(共2小题,27题8分,28题12分,共20分)
27.(1)证明:连接,
∵是直径, ∴,
又∵于, ∴,
B
D
O
H
C
EA
M
F
A
27题图
1
2
3
7
6
5
4
∵ ∴。 ······························1分
∵是的角平分线,
∴。 ····················…2分
又 ∵为的中点,
∴ 。 ·····················3分
∵于,
∵, 即。
又∵是直径, ∴是半圆的切线 ···4分
(2)∵,。
由(1)知,,∴。·····················5分
在中,于,平分,
∴,∴。········································6分
由∽,得。········································7分
y
x
O
B
M
N
C
A
图(1)
H
∴,∴。················8分
28.(1)∵,∴,。
∴,。····················1分
又∵抛物线过点、、,
故设抛物线的解析式为,
将点的坐标代入,求得。
∴抛物线的解析式为。········3分
(2)设点的坐标为(,0),过点作轴于点(如图(1))。
∵点的坐标为(,0),点的坐标为(6,0),
∴,。···························4分
∵,∴。
∴,∴,∴。·················5分
y
x
O
B
E
A
图(2)
D
∴
······6分
。
∴当时,有最大值4。
此时,点的坐标为(2,0)。··············7分
(3)∵点(4,)在抛物线上,
y
x
O
B
A
图(3)
D
∴当时,,
∴点的坐标是(4,)。
如图(2),当为平行四边形的边时,,
∵(4,),∴(0,),。
∴,。 ··········9分
① 如图(3),当为平行四边形的对角线时,
设,则平行四边形的对称中心为
(,0)。·················10分
∴的坐标为(,4)。
把(,4)代入,得。
解得 。
,。····················12分