中考复习专题1圆的切线 4页

中考复习专题1：圆的切线 （一） 重要考点 考点一：切线的性质 定理：圆的切线________于经过切点的半径．‎ 技巧：圆心与切点的连线是常用的辅助线．‎ 考点2　切线的判定 ‎ 定理：经过半径的外端并且________于这条半径的直线是圆的切线．‎ 证圆的切线技巧：‎ ‎(1)如果直线与圆有交点，连接圆心与交点的半径，证明直线与该半径垂直，即“有交点，作半径，证垂直”．‎ ‎(2)如果直线与圆没有明确的交点，则过圆心作该直线的垂线段，证明垂线段等于半径，即“无交点，作垂直，证半径”．‎ 考点3　切线长及切线长定理 ‎ 切线长 ‎ 在经过圆外一点的圆的切线上，这点和切点之间的线段的长，叫做这点到圆的切线长 ‎ 切线长定理 ‎ 从圆外一点引圆的两条切线，它们的切线长________，这一点和圆心的连线________两条切线的夹角 ‎ 基本图形 ‎ 如图所示，点P是⊙O外一点，PA，PB切⊙O于点 A，B，AB交PO于点C，则有如下结论：‎ ‎(1)PA＝PB；‎ ‎(2)∠APO＝∠BPO＝∠OAC＝∠OBC，∠AOP＝∠BOP＝∠CAP＝∠CBP ‎ 考点4　三角形的内切圆 ‎ 三角形的内切圆 ‎ 与三角形各边都相切的圆叫三角形的内切圆，这个三角形叫圆的外切三角形 ‎ 三角形的内心 ‎ 三角形内切圆的圆心叫做三角形的内心．它是三角形______________的交点，三角形的内心到三边的________相等 ‎ 基本规律 ‎⊙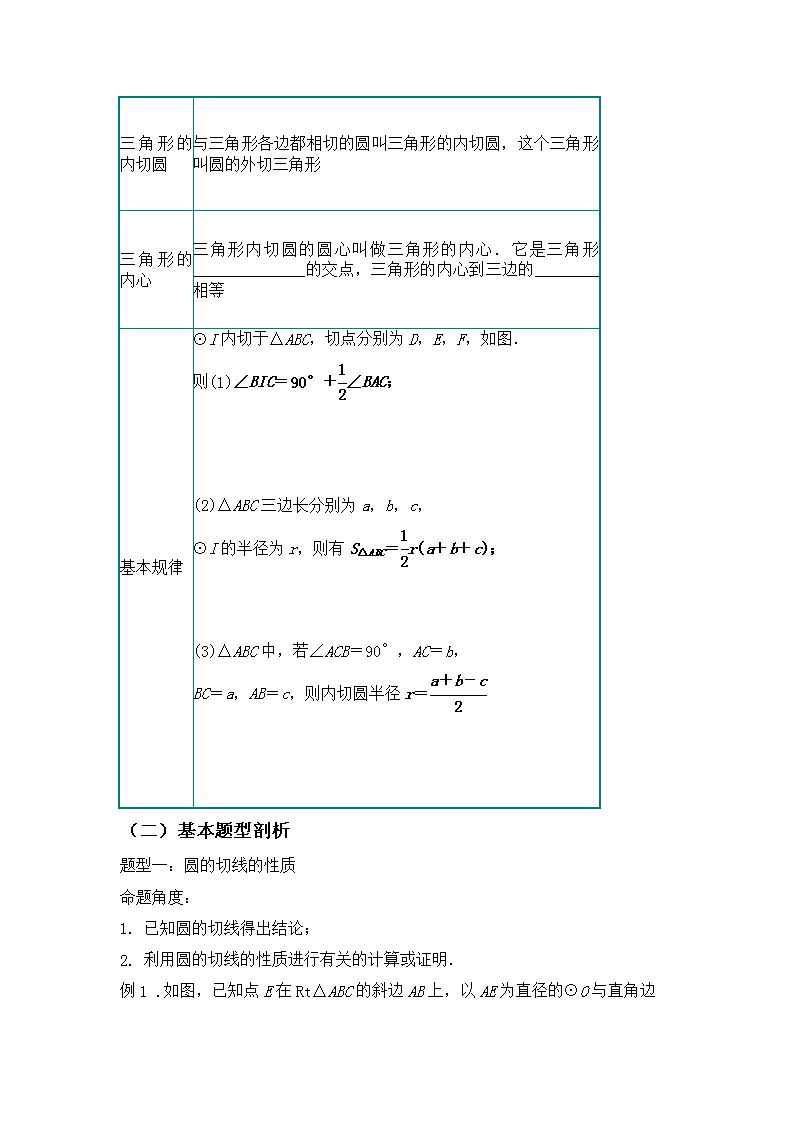I内切于△ABC，切点分别为D，E，F，如图．‎ 则(1)∠BIC＝90°＋∠BAC；‎ ‎(2)△ABC三边长分别为a，b，c，‎ ‎⊙I的半径为r，则有S△ABC＝r(a＋b＋c)；‎ ‎(3)△ABC中，若∠ACB＝90°，AC＝b，‎ BC＝a，AB＝c，则内切圆半径r＝ （一） 基本题型剖析 题型一：圆的切线的性质 ‎ 命题角度：‎ ‎1. 已知圆的切线得出结论；‎ ‎2. 利用圆的切线的性质进行有关的计算或证明．‎ 例1 .如图，已知点E在Rt△ABC的斜边AB上，以AE为直径的⊙O与直角边 BC相切于点D.‎ ‎(1)求证：AD平分∠BAC；‎ ‎(2)若BE＝2，BD＝4，求⊙O的半径．‎ 题型二：圆的切线的判定方法 命题角度：‎ ‎1．利用圆心到一条直线的距离等于圆的半径，判定这条直线是圆的切线；‎ ‎2．利用一条直线经过半径的外端，且垂直于这条半径，判定这条直线是圆的切线．‎ 例2. 如图，已知P是⊙O外一点，PO交⊙O于点C，OC＝CP＝2，弦AB⊥OC，劣弧的度数为120°，连接PB.‎ ‎(1)求BC的长；‎ ‎(2)求证：PB是⊙O的切线．‎ 题型三：切线长定理的运用 命题角度：‎ ‎1. 利用切线长定理计算；‎ ‎2. 利用切线长定理证明．‎ 例3.如图，PA、PB分别切⊙O于A、B两点，连接PO、AB相交于D，C是⊙O上一点，∠C＝60°.‎ ‎(1)求∠APB的大小；‎ ‎(2)若PO＝20 cm，求△AOB的面积．‎ 题型四：三角形的内切圆 命题角度：‎ ‎1. 三角形的内切圆的定义；‎ ‎2. 求三角形的内切圆的半径．‎ 例4.如图，Rt△ABC的内切圆⊙O与两直角边AB，BC分别相切于点D、E，过劣弧(不包括端点D、E)上任一点P作⊙O的切线MN，与AB，BC分别交于点M，N，若⊙O的半径为r，则Rt△MBN的周长为(　　) ‎ A．r B.r C．2r D.r ‎(三)练习 如图，△ABC内接于⊙O，∠B＝60°，CD是⊙O的直径，点P是CD延长线上的一点，且AP＝AC.‎ ‎(1)求证：PA是⊙O的切线；‎ ‎(2)若PD＝，求⊙O的直径．‎