中考数学圆压轴题带答案 9页

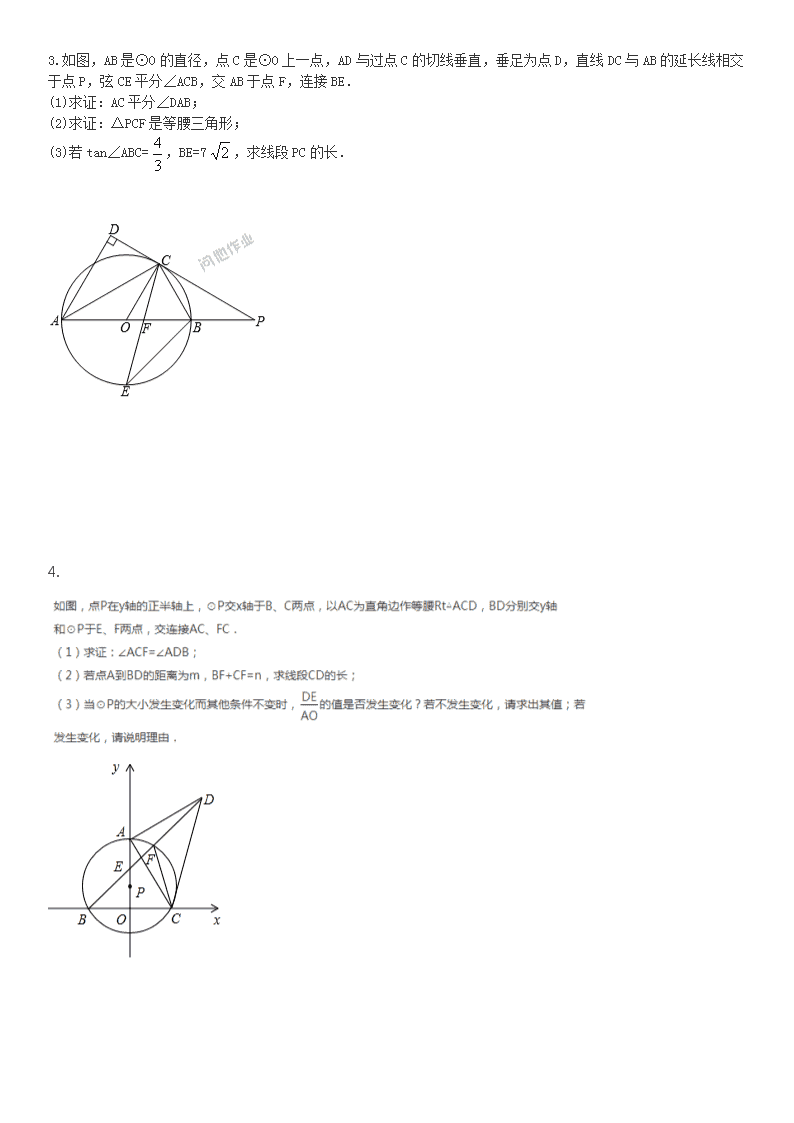
‎1.如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AC和BD相交于点E，且DC2=CE•CA．‎ ‎（1）求证：BC=CD；‎ ‎（2）分别延长AB，DC交于点P，过点A作AF⊥CD交CD的延长线于点F，若PB=OB，CD=，求DF的长．‎ ‎2.如图，AB是⊙O的直径，弦CD⊥AB于H，过CD延长线上一点E作⊙O的切线交AB的延长线于F．切点为G，连接AG交CD于K．    （1）求证：KE=GE；    （2）若=KD·GE，试判断AC与EF的位置关系，并说明理由；    （3） 在（2）的条件下，若sinE=，AK=，求FG的长．‎ ‎3.如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为点D，直线DC与AB的延长线相交于点P，弦CE平分∠ACB，交AB于点F，连接BE． (1)求证：AC平分∠DAB； (2)求证：△PCF是等腰三角形； (3)若tan∠ABC=，BE=7，求线段PC的长．‎ 4. ‎ ‎ ‎5.已知：如图，在半径为4的⊙O中，AB，CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC，连结DE，DE=。‎ （1） 求证：AM·MB=EM·MC；（2）求EM的长；（3）求sin∠EOB的值。 ‎ ‎ ‎ ‎6.如图，AE切⊙O于点E，AT交⊙O于点M，N，线段OE交AT于点C，OB⊥AT于点B，已知 ∠EAT=30°，AE=3，MN=2． （1）求∠COB的度数； （2）求⊙O的半径R； （3）点F在⊙O上（是劣弧），且EF=5，把△OBC经过平移、旋转和相似变换后，使它的两个顶点分别与点E，F重合．在EF的同一侧，这样的三角形共有多少个？你能在其中找出另一个顶点在⊙O上的三角形吗？请在图中画出这个三角形，并求出这个三角形与△OBC的周长之比．‎ ‎7.如图，AB是半径O的直径，AB=2．射线AM、BN为半圆O的切线．在AM上取一点D，连接BD交半圆于点C，连接AC．过O点作BC的垂线OE，垂足为点E，与BN相交于点F．过D点作半圆O的切线DP，切点为P，与BN相交于点Q． （1）求证：△ABC∽△OFB； （2）当△ABD与△BFO的面枳相等时，求BQ的长；‎ （3） 求证：当D在AM上移动时（A点除外），点Q始终是线段BF的中点 ‎ ‎ ‎ ‎ 8. 如图，在⊙O的内接△ABC中，∠ACB=90°，AC=2BC，过C作AB的垂线l交⊙O于另一点D，垂足为E.设P是 上异于A,C的一个动点，射线AP交l于点F，连接PC与PD，PD交AB于点G. （1）求证：△PAC∽△PDF； （2）若AB=5，，求PD的长； （3）在点P运动过程中，设，求与之间的函数关系式.（不要求写出的取值范围）‎ ‎ ‎ ‎1.‎ ‎【解答】：‎ ‎（1）证明：∵DC2=CE•CA，‎ ‎∴=，‎ ‎△CDE∽△CAD，‎ ‎∴∠CDB=∠DBC，‎ ‎∵四边形ABCD内接于⊙O，‎ ‎∴BC=CD；‎ ‎（2）解：如图，连接OC，‎ ‎∵BC=CD，‎ ‎∴∠DAC=∠CAB，‎ 又∵AO=CO，‎ ‎∴∠CAB=∠ACO，‎ ‎∴∠DAC=∠ACO，‎ ‎∴AD∥OC，‎ ‎∴=，‎ ‎∵PB=OB，CD=，‎ ‎∴=‎ ‎∴PC=4‎ 又∵PC•PD=PB•PA ‎∴PA=4也就是半径OB=4，‎ 在RT△ACB中，‎ AC===2，‎ ‎∵AB是直径，‎ ‎∴∠ADB=∠ACB=90°‎ ‎∴∠FDA+∠BDC=90°‎ ‎∠CBA+∠CAB=90°‎ ‎∵∠BDC=∠CAB ‎∴∠FDA=∠CBA 又∵∠AFD=∠ACB=90°‎ ‎∴△AFD∽△ACB ‎∴‎ 在Rt△AFP中，设FD=x，则AF=，‎ ‎∴在RT△APF中有，，‎ 求得DF=．‎ ‎2‎ 解：（1）如答图1，连接OG． ∵EG为切线，∴∠KGE+∠OGA=90°， ∵CD⊥AB，∴∠AKH+∠OAG=90°， 又OA=OG，∴∠OGA=∠OAG， ∴∠KGE=∠AKH=∠GKE，∴KE=GE． （2）AC∥EF，理由为： 连接GD，如答图2所示． ∵KG2=KDGE，即=， ∴=，又∠KGE=∠GKE， ∴△GKD∽△EGK， ∴∠E=∠AGD，又∠C=∠AGD， ∴∠E=∠C， ∴AC∥EF； （3）连接OG，OC，如答图3所示． sinE=sin∠ACH=，设AH=3t，则AC=5t，CH=4t， ∵KE=GE，AC∥EF，∴CK=AC=5t，∴HK=CK﹣‎ ‎ ‎ CH=t． 在Rt△AHK中，根据勾股定理得AH2+HK2=AK2， 即（3t）2+t2=（）2， 解得t=． 设⊙O半径为r， 在Rt△OCH中，OC=r，OH=r﹣3t，CH=4t， 由勾股定理得：OH2+CH2=OC2， 即（r﹣3t）2+（4t）2=r2，解得r=t=． ∵EF为切线，∴△OGF为直角三角形， 在Rt△OGF中，OG=r=，tan∠OFG=tan∠CAH==， ∴FG===．‎ ‎.‎ ‎4‎ ‎5.‎ ‎6.‎ ‎7.‎ ‎8.‎