中考数学专题复习与圆有关的计算 7页

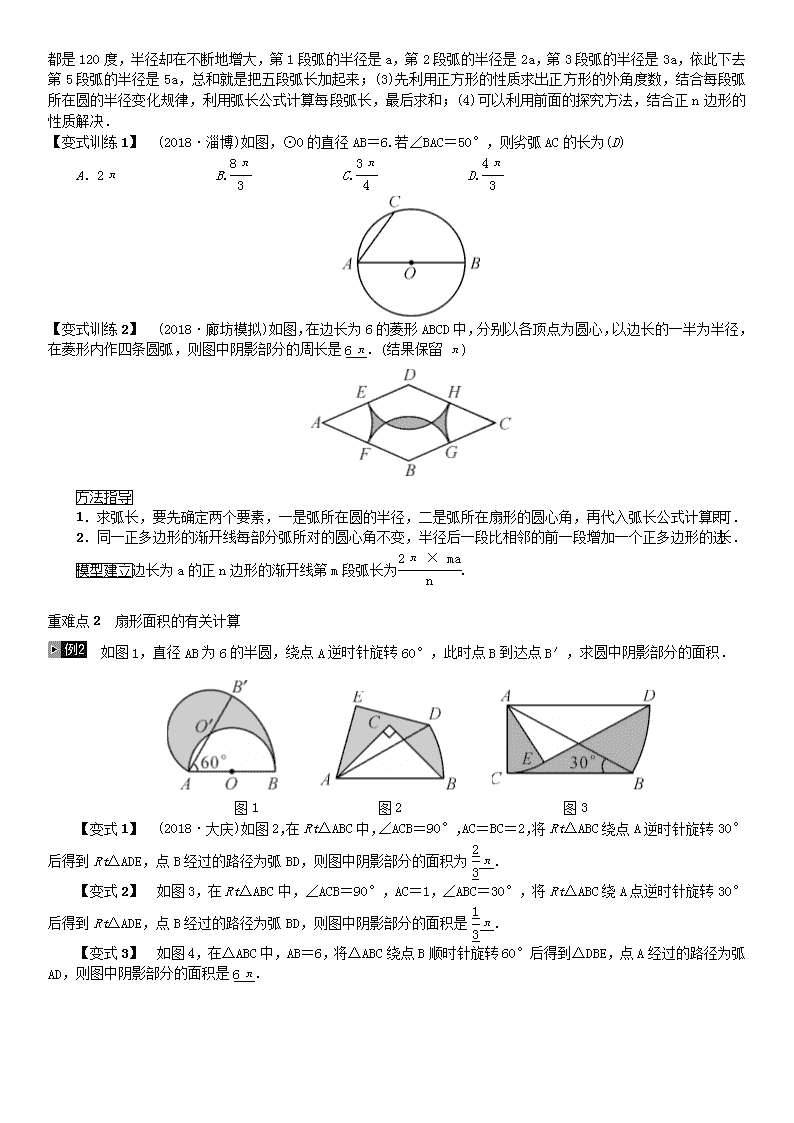
‎2019年中考数学专题复习 与圆有关的计算 命题点1　扇形弧长、面积的计算 ‎1．(2013·河北T14·3分)如图，AB是⊙O的直径，弦CD⊥AB，∠C＝30°，CD＝2.则S阴影＝(D)‎ A．π B．2π C. D.π ‎2．(2014·河北T19·3分)如图，将长为8 cm的铁丝首尾相接围成半径为2 cm的扇形．则S扇形＝4cm2.‎ 命题点2　正多边形与圆 ‎3．(2014·河北T15·3分)如图，边长为a的正六边形内有两个三角形(数据如图)，则＝(C)‎ A．3 B．4 C．5 D．6‎ 重难点1　弧长的计算 ‎　如图，△ABC是正三角形，曲线CDEFG…叫做“正三角形的渐开线”，曲线的各部分为圆弧．‎ ‎(1)图中已经有4段圆弧，请接着画出第5段圆弧GH；‎ ‎(2)设△ABC的边长为a，则第1段弧的长是；第5段弧的长是；前5段弧长的和(即曲线CDEFGH的长)是10πa；‎ ‎(3)类似地有“正方形的渐开线”“正五边形的渐开线”…，边长为a的正方形的渐开线的前5段弧长的和是；‎ ‎(4)猜想：‎ ‎①边长为a的正n边形的前5段弧长的和是；‎ ‎②边长为a的正n边形的前m段弧长的和是．‎ ‎【思路点拨】　(1)以点B为圆心，BG长为半径画弧即可；(2)利用弧长公式计算．但要先确定弧所对的圆心角都是120度，半径却在不断地增大，第1段弧的半径是a，第2段弧的半径是2a，第3段弧的半径是3a，依此下去第5段弧的半径是5a，总和就是把五段弧长加起来；(3)先利用正方形的性质求出正方形的外角度数，结合每段弧所在圆的半径变化规律，利用弧长公式计算每段弧长，最后求和；(4)可以利用前面的探究方法，结合正n边形的性质解决．‎ ‎【变式训练1】　(2018·淄博)如图，⊙O的直径AB＝6.若∠BAC＝50°，则劣弧AC的长为(D)‎ A．2π B. C. D. ‎【变式训练2】　(2018·廊坊模拟)如图，在边长为6的菱形ABCD中，分别以各顶点为圆心，以边长的一半为半径，在菱形内作四条圆弧，则图中阴影部分的周长是6π．(结果保留π)‎ ‎1．求弧长，要先确定两个要素，一是弧所在圆的半径，二是弧所在扇形的圆心角，再代入弧长公式计算即可．‎ ‎2．同一正多边形的渐开线每部分弧所对的圆心角不变，半径后一段比相邻的前一段增加一个正多边形的边长．‎ 边长为a的正n边形的渐开线第m段弧长为.‎ 重难点2　扇形面积的有关计算 ‎　如图1，直径AB为6的半圆，绕点A逆时针旋转60°，此时点B到达点B′，求圆中阴影部分的面积．‎ ‎ ‎ 图1 图2 　　　图3‎ ‎【变式1】　(2018·大庆)如图2，在Rt△ABC中，∠ACB＝90°，AC＝BC＝2，将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE，点B经过的路径为弧BD，则图中阴影部分的面积为π．‎ ‎【变式2】　如图3，在Rt△ABC中，∠ACB＝90°，AC＝1，∠ABC＝30°，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为弧BD，则图中阴影部分的面积是π．‎ ‎【变式3】　如图4，在△ABC中，AB＝6，将△ABC绕点B顺时针旋转60°后得到△DBE，点A经过的路径为弧AD，则图中阴影部分的面积是6π．‎ ‎ ‎ 图4 　　　　图5‎ ‎【变式4】　如图5，在Rt△ABC中，∠ACB＝90°，BC＝1，将Rt△ABC绕点C顺时针旋转60°，此时点B恰好在DE上，其中点A经过的路径为弧AD，则图中阴影部分的面积是－．(注：所有小题结果保留π)‎ ‎【思路点拨】　阴影部分的面积可以看作以旋转点为圆心，旋转角为圆心角，AB为半径的扇形面积；只有变式4阴影部分的面积是S扇形ACD－S△BCE.‎ ‎【自主解答】　解：∵AB＝AB′＝6，∠BAB′＝60°，‎ ‎∴S阴影＝S扇形B′AB＋S半圆O′－S半圆O＝S扇形B′AB＝×π×62＝6π.‎ 在圆中求阴影部分面积大致有以下方法：‎ ‎(1)弓形或弓形的一部分可转化成扇形减去三角形的面积；‎ ‎(2)新月形可以用扇形减去一个弓形的面积；‎ ‎(3)可以利用等积变换求阴影部分的面积；‎ ‎(4)可以利用轴对称、中心对称求阴影部分的面积；‎ ‎(5)旋转形成阴影部分的面积，往往可以转化成求一个扇形的面积．‎ 重难点3　正多边形和圆 ‎　(2017·河北模拟)如图是由有两个公共顶点的正六边形与正方形组成的一个图形．若阴影部分的周长为10，则这个图形的外轮廓线的周长为(A)‎ A．18 B．18 C．22 D．22 ‎【思路点拨】　从图形上能看出，正方形的边长等于正六边形边长的2倍．‎ 提示：设正六边形的边长为a，则正方形的边长为2a，由题意，得5a＝10，解得a＝2.则外轮廓线的周长为3a＋2a×3＝9a＝18.‎ ‎【变式训练3】　(2017·河北模拟)如图，正六边形与正方形有重合的中心O.若∠BOC是正n边形的一个外角，则n的值为(C)‎ A．8 B．10 C．12 D．16‎ ‎【变式训练4】　(2018·石家庄二模)正六边形ABCDEF与正三角形△ACG按如图所示位置摆放，在六边形AGCDEF中，的值是(D)‎ A. B. C. D. ‎1．熟悉常见正多边形边长与对角线的数量关系．‎ ‎2．正n边形的中心角与每一个外角相等，都等于(n≥3)．‎ ‎3．研究面积相关问题时可采用割补与拼接等方法，研究周长可采用化曲为直等方法．‎ 注：正多边形与圆中，正多边形通常是指正方形，正五边形，正六边形，正八边形等常见的正多边形．‎ ‎1．(2018·盘锦)如图，一段公路的转弯处是一段圆弧()，则的展直长度为(B)‎ A．3π m B．6π m C．9π m D．12π m ‎2．(2018·成都)如图，在▱ABCD中，∠B＝60°，⊙C的半径为3，则图中阴影部分的面积是(C)‎ A．π B．2π C．3π D．6π ‎3．(2018·德州)如图，从一块直径为2 m的圆形铁皮上剪出一个圆心角为90°的扇形，则此扇形的面积为(A)‎ A. m2 B.π m2 C．π m2 D．2π m2‎ ‎4．(2018·河北模拟)如图，分别把正六边形边AB，EF，CD向两个方向延长，相交于点M，N，Q，则阴影部分与空白部分的面积比为(A)‎ A. B. C. D. ‎5．(2018·河北模拟)如图，六边形ABCDEF和六边形MNPQGH都是正六边形．若AB＝10，则MN的值可能是(D)‎ A. B．5 C．5 D．5 ‎6．(2018·株洲)如图，正五边形ABCDE和正三角形AMN都是⊙O的内接多边形，则∠BOM＝48°．‎ ‎7．(2018·石家庄藁城区模拟)如图，M，N分别是正五边形ABCDE的边AB，AE的中点，四边形MNHG是位于该正五边形内的正方形，则∠BMH的度数是99°．‎ ‎8．(2018·盐城)如图，图1是由若干个相同的图形(图2)组成的美丽图案的一部分，图2中图形的相关数据：半径OA＝2 cm，∠AOB＝120°.则图2的图形周长为cm(结果保留π)．‎ ‎9．(2018·河南)如图，在△ABC中，∠ACB＝90°，AC＝BC＝2，将△ABC绕AC的中点D逆时针旋转90°得到△A′B′C′，其中点B的运动路径为，则图中阴影部分的面积为π－．‎ ‎10．(2018·邢台宁晋县模拟)如图，半圆O的直径AB＝4，P，Q是半圆O上的点，弦PQ的长为2，则与的长度之和为(B)‎ A.π B.π C.π D．π 提示：连接OP，OQ，易知△OPQ为等边三角形，l＋l＝×π×2＝π.‎ ‎11．(2018·威海)如图，在正方形ABCD中，AB＝12，点E为BC的中点，以CD为直径作半圆CFD，点F为半圆的中点，连接AF，EF，则图中阴影部分的面积是(C)‎ A．18＋36π B．24＋18π C．18＋18π D．12＋18π ‎　　‎ 提示：作FH⊥BC交BC延长线于点H，连接AE，‎ S阴影＝S正方形ABCD＋S半圆－S△ABE－S△AEF＝12×12＋×π×62－×12×6－×6×6＝18＋18π.‎ ‎12．(2018·河北模拟)如图，点P是⊙O外一点，PA切⊙O于点A，AB是⊙O的直径，连接OP，过点B作BC∥OP交⊙O于点C，连接AC交OP于点D.‎ ‎(1)求证：PC是⊙O的切线；‎ ‎(2)若PD＝ cm，AC＝8 cm，则图中阴影部分的面积为 cm2；‎ ‎(3)在(2)的条件下，若点E是的中点，连接CE，求CE的长．‎ 解：(1)证明：连接OC，‎ ‎∵PA切⊙O于点A，‎ ‎∴∠PAO＝90°.‎ ‎∵OP∥BC，‎ ‎∴∠AOP＝∠OBC，∠COP＝∠OCB.‎ ‎∵OC＝OB，∴∠OBC＝∠OCB.‎ ‎∴∠AOP＝∠COP.‎ 在△PAO和△PCO中， ‎∴△PAO≌△PCO(SAS)．‎ ‎∴∠PAO＝∠PCO＝90°.‎ 又∵OC是⊙O的半径，‎ ‎∴PC是⊙O的切线．‎ ‎(3)连接AE，BE，过点B作BM⊥CE于点M，‎ ‎∴∠CMB＝∠EMB＝90°，∠AEB＝90°.‎ 又∵点E是的中点，∴＝. ‎ ‎∴∠ECB＝∠ACE＝∠ACB＝45°.‎ 又∵∠CMB＝90°，‎ ‎∴∠CBM＝45°.∴BM＝CM.‎ 在Rt△BCM中，由勾股定理，得CM2＋BM2＝BC2，即CM2＋BM2＝36，‎ ‎∴CM＝BM＝3 cm.‎ ‎ 又∵∠ABE＝∠ACE＝45°，‎ ‎∴在Rt△AEB中，BE＝AB·cos∠ABE＝5 cm.‎ 在Rt△BEM中，由勾股定理，得 EM＝＝＝4(cm)，‎ ‎∴CE＝CM＋EM＝7 cm，‎ 即CE的长为7 cm.‎