中考中档题训练 9页

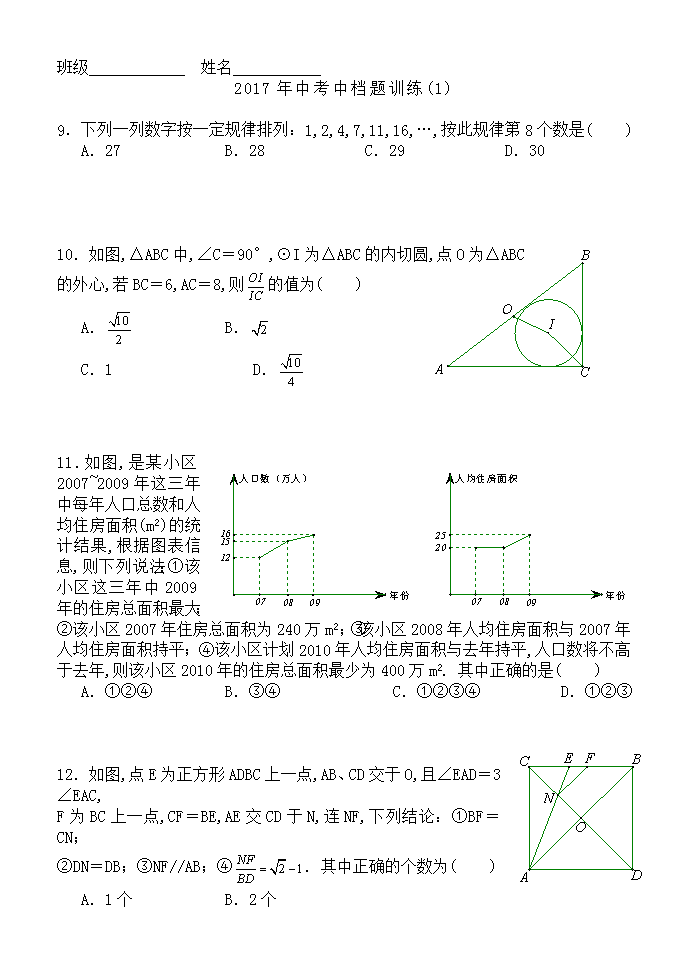
班级 姓名 ‎ ‎2017年中考中档题训练(1)‎ ‎9．下列一列数字按一定规律排列：1,2,4,7,11,16,…,按此规律第8个数是( )‎ ‎ A．27 B．‎28 ‎ C．29 D．30‎ ‎10．如图,△ABC中,∠C＝90°,⊙I为△ABC的内切圆,点O为△ABC 的外心,若BC＝6,AC＝8,则的值为( )‎ ‎ A． B． ‎ C．1 D．‎ ‎11．如图,是某小区2007~2009年这三年中每年人口总数和人均住房面积(m2)的统计结果,根据图表信息,则下列说法：①该小区这三年中2009年的住房总面积最大；②该小区2007年住房总面积为240万m2；③该小区2008年人均住房面积与2007年人均住房面积持平；④该小区计划2010年人均住房面积与去年持平,人口数将不高于去年,则该小区2010年的住房总面积最少为400万m2. 其中正确的是( )‎ ‎ A．①②④ B．③④ C．①②③④ D．①②③‎ ‎12．如图,点E为正方形ADBC上一点,AB、CD交于O,且∠EAD＝3∠EAC,‎ F为BC上一点,CF＝BE,AE交CD于N,连NF,下列结论：①BF＝CN；‎ ‎②DN＝DB；③NF//AB；④. 其中正确的个数为( ) ‎ ‎ A．1个 B．2个 ‎ C．3个 D．4个 ‎15．在平面直角坐标系中,直线y=kx+3向左平移1个单位正好经过点(－2,0),则不等式kx>3的解集为 . ‎ ‎16．直线与坐标轴交于A、B两点,矩形ABCD对称中心为,双曲线正好经过C,两点,则k= . ‎ ‎22．如图,AB,CD是⊙O的两条直径,点M为OB的中点,CM的延长线交⊙O于N,且NM>MC,连DN、BN ‎(1)求证：MN·CN=3BM2；‎ ‎(2)若⊙O的半径为4,,求S△BMN的值. 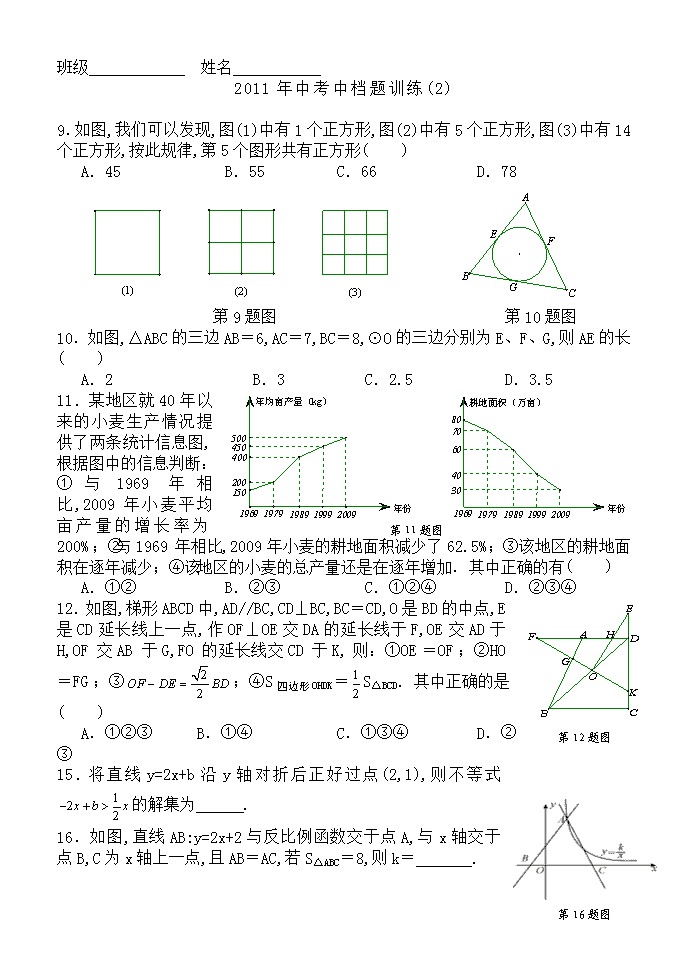‎ 班级 姓名 ‎ ‎2011年中考中档题训练(2)‎ ‎9．如图,我们可以发现,图(1)中有1个正方形,图(2)中有5个正方形,图(3)中有14个正方形,按此规律,第5个图形共有正方形( )‎ ‎ A．45 B．‎55 ‎ C．66 D．78‎ ‎ ‎ 第9题图 第10题图 ‎10．如图,△ABC的三边AB＝6,AC＝7,BC＝8,⊙O的三边分别为E、F、G,则AE的长( )‎ ‎ A．2 B．‎3 ‎ C．2.5 D．3.5‎ 第11题图 ‎11．某地区就40年以来的小麦生产情况提供了两条统计信息图,根据图中的信息判断：①与1969年相比,2009年小麦平均亩产量的增长率为200%；②与1969年相比,2009年小麦的耕地面积减少了62.5%；③该地区的耕地面积在逐年减少；④该地区的小麦的总产量还是在逐年增加. 其中正确的有( )‎ ‎ A．①② B．②③ C．①②④ D．②③④‎ 第12题图 ‎12．如图,梯形ABCD中,AD//BC,CD⊥BC,BC＝CD,O是BD的中点,E是CD延长线上一点,作OF⊥OE交DA的延长线于F,OE交AD于H,OF交AB于G,FO的延长线交CD于K,则：①OE＝OF；②HO＝FG；③；④S四边形OHDK＝S△BCD. 其中正确的是( )‎ ‎ A．①②③ B．①④ C．①③④ D．②③‎ 第16题图 ‎15．将直线y=2x+b沿y轴对折后正好过点(2,1),则不等式的解集为 . ‎ ‎16．如图,直线AB:y=2x+2与反比例函数交于点A,与x轴交于点B,C为x轴上一点,且AB＝AC,若S△ABC＝8,则k＝ . ‎ ‎22．如图,⊙O内接四边形ABCD,AB为⊙O的直径,AE⊥CD于E,BF⊥CD于F. ‎ ‎(1)求证：DE＝CF；‎ ‎(2)若DE＝1,CD＝6,AE＝7,求⊙O的半径. ‎ ‎23．某商品的进价为每件8元,如果售价为每件10元,每月可卖300件,如果售价超过10元但不超过20元,每件商品的售价每上涨1元,则每月少卖5件,如果超过20元后,若再涨价,则每涨1元,每月少卖10件,设每件商品涨价x元(x为正整数),每月的销售量为y件. ‎ ‎(1)求y与x的函数关系式并直接写出自变量x的取值范围；‎ ‎(2)设每月销售利润为W元,请直接写出W与x的函数关系式；‎ ‎(3)每件商品的售价定为多少时,每月可获得最大利润,最大利润是多少？‎ ‎ 2011年中考基础训练(1)‎ ‎1．－3的相反数是( )‎ ‎ A． B．‎3 ‎ C． D．－3‎ ‎2．函数中自变量x的取值范围是( )‎ ‎ A．x≥4 B．x≥－‎4 ‎ C．x≤4 D．x≤－4‎ ‎3．解集在数轴上表示如图的不等式组为( )‎ ‎ A． B． C． D．‎ ‎4．下列说法：①小芳前几次的体育测试成绩都是“优秀”, 那么她这次测试一定为“优秀”；‎ ‎②随意掷一枚骰子, “掷得的数是奇数”的概率与“掷得的数字是偶数”的概率相等, 其中( )‎ ‎ A．①②都正确 B．只有①正确 C．只有②正确 D．两个说法都错误 ‎5．2010年世博会‎5月1日在上海举行, 当天园区各展馆共接待中外游客约20.56万人, 这个数用科学记数法表示为( )‎ ‎ A．2.1×106人 B．2.056×105人 C．20.56×104人 D．2.056×107人 ‎6．如图, △ABC中, 点D为BC上一点, 将△ADC沿直线AD折叠, 点C恰好落在AB上的点E处, ∠B＝30°, ∠BDE＝40°, 则∠BAC的度数是( )‎ ‎ A．60° B．72° ‎ C．75° D．80°‎ ‎7．由一些大小相同的小正方体组成的简单几何体的主视图和俯视图如下图, 那么后面三个视图可以作为这个几何体的左视图的是( )‎ A．(1)(2)(3) B．(1)(2) C．(1)(3) D．(2)(3)‎ ‎8．若x1, x2为一元二次方程x2－2x－8＝0的两个根, 则x1+x2的值是( )‎ ‎ A．－2 B．－‎8 ‎ C．2 D．8‎ ‎13．计算, cos30°＝ , , . ‎ ‎14．如果四个整数数据中的三个分别是6, 8, 8, 且这四组数据的众数和平均数相等, ‎ 则这四个数整数数据中最大的数为 . ‎ ‎17．解方程. ‎ ‎18．先化简, 再求值：, 其中. ‎ ‎19．如图, 已知AB＝AC, BD＝CE, 点O、E分别在AB、AC上, ‎ 求证：BE＝CD. ‎ ‎20．阳阳和光光玩扑克游戏, 4张大小质地均相同的卡片上分别标有1, 2, 3, 4, 现将标有数字的一面朝下, 扣在桌面上, 请1人从中摸出两张牌, 如果至少有1个, 则阳阳胜, 如果没有摸到1, 则光光胜, 他们设计了A、B两种摸牌方案, A：一次摸两张牌；B：摸一张牌后放回, 重新洗匀, 再摸一张, 请你分别用画树状图和列表求出A、B两方案阳阳胜的概率, 并判断哪种方案对阳阳更有利. ‎ ‎21．如图, 已知网格中每个小正方形边长为1, 图形阴影图案是由两段以格点为圆心, 分别以小正方形的边长和对角线长为半径的圆弧和网格边围成. ‎ ‎(1)图中阴影部分的面积是 (结果保留)；‎ ‎(2)请以阴影图案为基本图案, 借助轴对称, 平移或旋转设计一个完美的图案(至少含两种图形变换). ‎ 班级 姓名 ‎ ‎2011年中考基础训练(2)‎ ‎1．－3的倒数是( )‎ ‎ A．3 B． C．－3 D．‎ ‎2．函数中自变量x的取值范围是( )‎ ‎ A．x≤2 B．x<‎2 ‎ C．x≥2 D．x>2‎ ‎3．不等式组的解集在数轴上表示正确的是( )‎ A B C D ‎4．下列说法：①方程ax2+bx+c＝0有实根；②掷一枚普通骰子, 朝上一面的点数是8, 其中是不可能事件的是( )‎ ‎ A．①② B．① C．② D．都不是 ‎5．国家游泳中心——“水立方”的外层膜的展开面积约260000平方米, 将260000用科学记数法表示应为( )‎ ‎ A．26×104 B．2.6×‎106 ‎ C．0.26×106 D．2.6×105‎ ‎6．如图, AB＝AC＝AD＝BE＝CE, ∠E＝70°, 则∠BDC的大小是( )‎ ‎ A．20° ‎ B．30° ‎ C．25° ‎ D．35°‎ ‎7．下图是由4个相同的小正方体叠成的一个立体图形, 那么它的左视图是( )‎ ‎8．若x1, x2为一元二次方程＝0的两个根, 则x1, x2的值是( )‎ ‎ A．－3 B．‎3 ‎ C．4 D．－4‎ ‎13．计算：sin45°＝ , , . ‎ ‎14．某五天的气温如下：20, 23, x, 19, 24, 温度都是正整数(单位：°C), 其中x是众数, 已知这组数据的众数小于平均数, 则x= . ‎ ‎17．解方程：. ‎ ‎18．先化简, 再求值：, 其中. ‎ ‎19．如图, △ABC中, ∠BAC＝90°, AD⊥BC于D, 求证：AD2＝BD·CD. ‎ ‎20．小明和小王玩一种摸球游戏：一布袋中装有4个颜色大小完全相同的小球, 分别标有数字1, －1, 2, 3, 请一人从布袋中摸出两个球, 如果上面的数字之和为奇数, 则小明胜, 否则小王胜, 为此, 两人设计了甲、乙两种方案, 甲方案：一次摸两个球；乙方案：先摸一个球, 放回摇匀, 再摸出一个, 请你分别利用画树状图和列表法求出甲、乙两个方案中小王胜的概率, 并判断哪种方案对小王更有利. ‎ ‎21．如图, 已知网格中每个小正方形的边长都是1, 图中的阴影图案是由两条以格点为圆心, 半径分别为1和2的圆弧和两条线段围成的. ‎ ‎(1)图中阴影部分的面积是 ；‎ ‎(2)请你在网格中以阴影图案为基本图案, 借助轴对称平移或旋转设计一个完整的图案(至少含有两种图形变换). ‎