上海中考数学一模题汇编含答案 23页

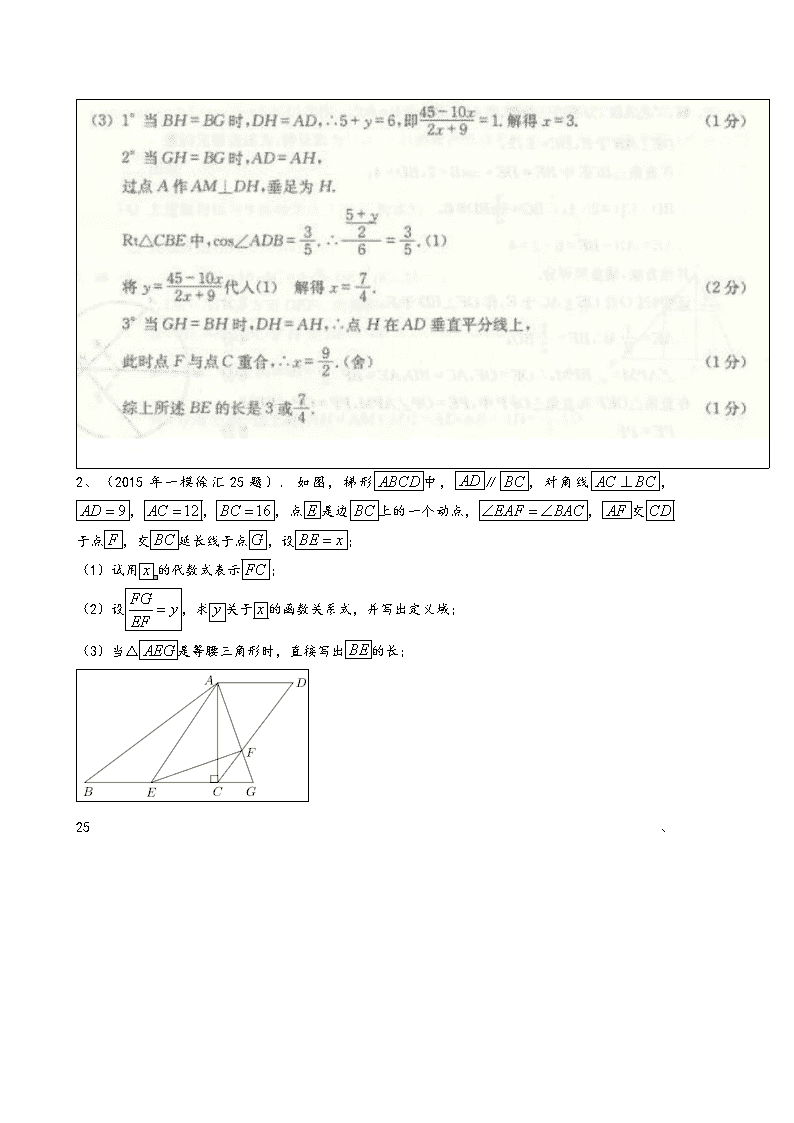
‎2015年上海一模25题集锦 ‎1、(2015年一模黄浦25题）‎ ‎2、（2015年一模徐汇25题）. 如图，梯形中，∥，对角线，，，，点是边上的一个动点，，交于点，交延长线于点，设；‎ ‎（1）试用的代数式表示；‎ ‎（2）设，求关于的函数关系式，并写出定义域；‎ ‎（3）当△是等腰三角形时，直接写出的长；‎ ‎[来源:学.科.网]‎ ‎25、‎ 所以，BE＝7‎ ‎3（2015年一模宝山26题）. 如图在△中，，，为边上一动点（和、‎ 不重合），过作∥交AC于，并以为边向一侧作正方形，设 ‎，‎ ‎（1）请用的代数式表示正方形的面积，并求出当边落在边上时的的值；‎ ‎（2）设正方形与△重合部分的面积为，求关于的函数及其定义域；‎ ‎（3）点在运动过程中，是否存在、、三点中的两点落在以第三点为圆心的圆上 的情况？若存在，请直接写出此时的值，若不存在，则请说明理由；‎ ‎4、（2015年一模崇明25题）（本题满分14分，其中第(1)小题5分，第(2)小题5分，第(3)小题4分）‎ ‎ 已知在中，，，O为边AB上一动点（不与A、B重合），以O为圆心OB为半径的圆交BC于点D，设，．‎ ‎（1）如图１，求y关于x的函数关系式及定义域；‎ ‎（2）当⊙O与线段AC有且只有一个交点时，求x的取值范围；‎ ‎（3）如图２，若⊙O与边AC交于点E（有两个交点时取靠近C的交点），联结DE，‎ 当与相似时，求x的值.‎ C A D O B ‎·‎ ‎·‎ ‎·‎ ‎（图1）‎ ‎ ‎ B C A ‎（备用图1）‎ E C A D O B ‎·‎ ‎·‎ ‎·‎ ‎·‎ ‎（图2）‎ B C25模联考XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX A ‎（备用图2）‎ ‎5．（2015一模奉贤25题）（本题满分14分，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分4分）‎ A B D G C E F 第25题图 已知：矩形ABCD中，过点B作 BG⊥AC交AC于点E，分别交射线AD于F点、交射线CD于G点，BC＝6．‎ ‎（1）当点F为AD中点时，求AB的长；‎ ‎（2）联结AG，设AB＝x，S⊿AFG=y,求y关于x的函数关系式及自变量x的取值范围；‎ ‎（3）是否存在x的值，使以D为圆心的圆与BC、BG都相切？若存在，‎ 求出x的值；若不存在，请说明理由．‎ ‎25．解：（1）∵点F为AD中点，且AD=BC=6，∴AF=3…………………………………（1分） ∵矩形ABCD中，∠ABC=90°,BG⊥AC于点E，∴∠ABE+∠EBC=90°,∠ACB+∠EBC=90° ∴∠ABE=∠ACB，∴△ABF∽△BCF………………………………………（2分）‎ ‎∴∴ AB=………………………………………………（1分）‎ ‎(2)由（1）可得△ABF∽△BCF∴∵AB＝x，BC＝6 ∴AF=……（1分）‎ 同理可得：CG=………………………………………（1分）‎ ①当F点在线段AD上时DG=CG-CD=‎ ‎∴S⊿AFG=即……………………（2分）‎ ②当F点在线段AD延长线上时，DG=CD-CG =‎ ‎∴S⊿AFG=即……（2分）‎ ‎（3）过点D作DH⊥BG于点H ‎∵以点D为圆心的圆与BC、BG都相切∴CD=DH∴∠DBF=∠CBD……………（1分）‎ ‎∵矩形ABCD中,∠ACB=∠CBD……………………………（1分）‎ ‎∴Rt△BEC中，∠ACB+∠CBD+∠DBF=90°∴∠ACB =30°……（1分）‎ ‎∴Rt△ABC中，tan∠ACB=∴tan30°=∴……………（1分）‎ 即当时，以点D为圆心的圆与BC、BG都相切。‎ ‎6．（2015年一模虹口25题）（本题满分14分，第（1）小题满分4分，第（2）小题满分4分，第（3）小题满分6分）‎ 如图，在等腰梯形ABCD中，AD//BC，AB=CD，AD=6，BC=24，，点P在边BC上，BP=8，点E在边AB上，点F在边CD上，且∠EPF=∠B．过点F作FG⊥PE交线段PE于点G，设BE＝x，FG＝y．‎ ‎（1）求AB 的长；‎ ‎（2）当EP⊥BC时，求y的值；‎ ‎（3）求y与x的函数关系式，并写出x的取值范围.‎ F P E C A B G 第25题图 D P C A B 备用图 D ‎7．（本题满分14分，其中第（1）小题4分，第（2）小题5分，第（3）小题5分）‎ 已知在△中，，，点是边上的一个动点，，∥，联结．‎ ‎（1）如图10，如果∥，求的长；‎ ‎（2）如图11，如果直线与边的延长线交于点，设，，求关于的函数解析式，并写出它的定义域；‎ ‎（3）如图12，如果直线与边的反向延长线交于点，联结，当△与 ‎△相似时，试判断线段与线段的数量关系，并说明你的理由．‎ A B C D P 图12‎ F A B C D P 图10‎ B A C D P 图11‎ E ‎8．（2015年一模金山25题）（本题满分14分）‎ 如图，在中，，，点、分别在边、上（点不与点、重合）∥．把沿直线翻折，点与点重合，设．‎ ‎（1）求的余切值；‎ A E C B F ‎（2）当点在的外部时，、分别交于、，若，求关于的函数关系式并写出定义域；‎ ‎（3）（下列所有问题只要直接写出结果即可）‎ 以为圆心、长为半径的⊙与边 ‎①没有公共点时，求的取值范围．‎ ‎②一个公共点时，求的取值范围．‎ ‎③两个公共点时，求的取值范围． ‎ ‎9（2015年一模静安青浦25题）‎ ‎10.（2015年一模普陀25题） 如图，等边△，，点是射线上的一动点，联结，作的垂直平分线交线段于点，交射线于点，分别联结，‎ ‎（1）当点在线段的延长线上时，‎ ‎① 求的度数，并求证：△∽△‎ ‎② 设，，求关于的函数解析式，并写出它的定义域 ‎（2）如果△是等腰三角形，求△的面积 ‎ ‎ ‎11．（2015年一模闸北25题）（本题满分14分 ，第（1）小题5分，第（2）小题5分，第（3）小题4分）‎ A B C D E K F 图10‎ 如图10，已知在等腰 Rt△ABC中，∠C＝90°，斜边AB＝2，若将△ABC翻折，折痕EF分别交边AC、边BC于点E和点F（点E不与A点重合，点F不与B点重合），且点C落在AB边上，记作点D．过点D作DK⊥AB，交射线AC于点K，设AD＝x，y＝cot∠CFE，‎ ‎（1）求证：△DEK∽△DFB； ‎ ‎（2）求y关于x的函数解析式并写出定义域； ‎ A B C 备用图 A B C 备用图 ‎（3）联结CD，当＝时，求x的值 ‎12.（2015年一模长宁25题） （本题满分14分）‎ 如图，已知△ABC是等边三角形，AB=4，D是AC边上一动点（不与A、C重合），EF垂 直平分BD，分别交AB、BC于点E、F，设CD=x，AE=y.‎ （1） 求证：△AED∽△CDF；‎ （2） 求y关于x的函数关系式，并写出定义域；‎ （3） 过点D作DH⊥AB，垂足为点H，当EH=1时，求线段CD的长.‎ ‎13（2015年六区联考25题）. 已知在矩形中，是边上的一动点，联结、，过点作射线交线段的延长线于点，交边于点，且使得，如果，，，；[来源:学+科+网]‎ ‎（1）求关于的函数解析式，并写出它的定义域；‎ ‎（2）当时，求的正切值；‎ ‎（3）如果△是以为底角的等腰三角形，求的长；‎ ‎25.解：（1）在矩形ABCD中， ∵AD∥BC，∴∠APB=∠CBP. ∵∠ABE=∠CBP，∴∠APB=∠ABE. ∵∠A=∠A，∴△ABP∽△AMB.…………………………………………………（1分） ∴ . ∵AB=2，AP=x，PM=y，∴ .…………………………………………（1分） ∴所求函数的解析式为 .…… …………………………………………（1分） 定义域为 .…………………………………………………………………（1分） （2）∵AP=4，∴MP=3.…………………………………………………………（1分） ∵AP=4，AD=5，∴PD=1.∴ . ∵∠A=∠D，∴△ABP∽△DPC. ∴∠APB=∠DCP. ∵∠DPC+∠DCP=90°，∴∠DPC+∠APB=90°. ∴∠BPE=∠BPC=90°.……………………………………………………………（1分） ∵AD∥BC，∴ ，即 . 解得 .……………………………………………………………………（1分） 又∵AP=4，AB=2，∴ . ∴ .……………………………………………………………（1分） 另解：作MH⊥BP，垂足为点H. ∵AP=4，∴MP=3.…………………………………………………………………（1分） ∵AP=4，AB=2，∴ . ‎ 由△BPM的面积，可得 ，即 . 解得 .…………………………………………………………………（1分） ∵AM=1，AB=2，∴ . ∴ .………………………………………………………………………（1分） ∴ .…………………………………………………………（1分） （3）（i）当∠EBC=∠ECB时，可得∠AMB=∠DPC，△AMB≌△DPC. ∴AM=DP.…………………………………………………………………………（1分） ∴x+x-y=5，即 .…………………………………………………………（1分） 解得x=4或x=1（不符合题意，舍去）.…………………………………………（1分） （ii）当∠EBC=∠BEC时，可得EC=BC=5，PE=PM =y.………………………（1分） ∴ . 整理，得3x2-10x-4=0.……………………………………………………………（1分） 解得 或 （不符合题意，舍去）. ………………………（1分） 综上所述，AP的长为4或 .‎ 欢迎您的光临，Word文档下载后可修改编辑.双击可删除页眉页脚.谢谢！希望您提出您宝贵的意见，你的意见是我进步的动力。赠语； 1、如果我们做与不做都会有人笑，如果做不好与做得好还会有人笑，那么我们索性就做得更好，来给人笑吧！ 2、现在你不玩命的学，以后命玩你。3、我不知道年少轻狂，我只知道胜者为王。4、不要做金钱、权利的奴隶；应学会做“金钱、权利”的主人。5、什么时候离光明最近？那就是你觉得黑暗太黑的时候。6、最值得欣赏的风景，是自己奋斗的足迹。 7、压力不是有人比你努力，而是那些比你牛×几倍的人依然比你努力。‎