2019年上海中考数学二模汇编 第25题 12页

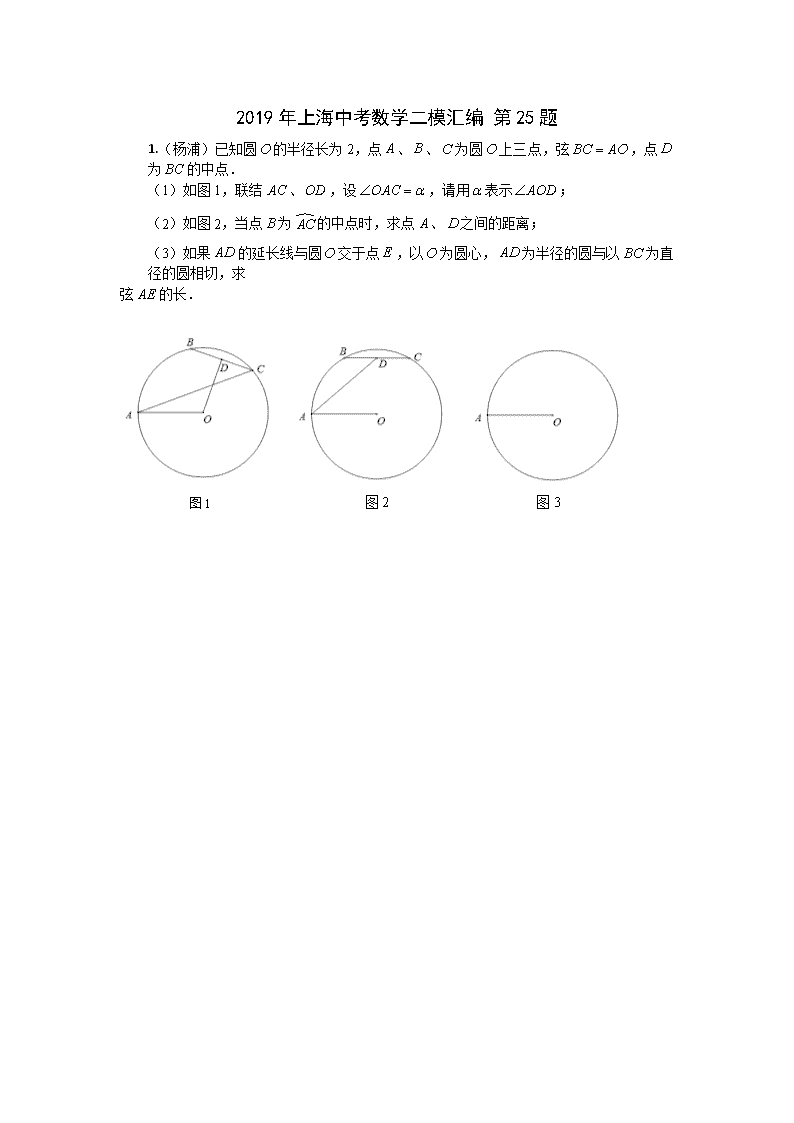
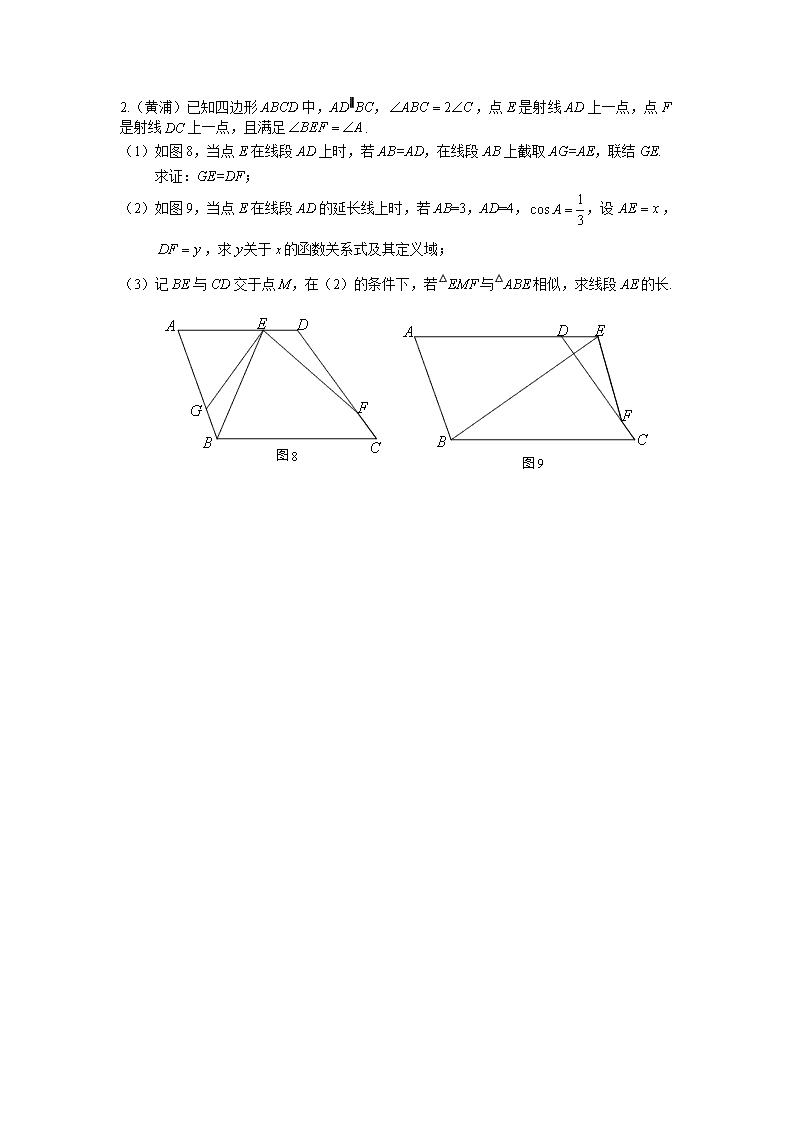
2019 年上海中考数学二模汇编 第 25 题 1.（杨浦）已知圆 的半径长为 2，点 、 、 为圆 上三点，弦 ，点 为 的中点． （1）如图 1，联结 、 ，设 ，请用 表示 ； （2）如图 2，当点 为 的中点时，求点 、 之间的距离； （3）如果 的延长线与圆 交于点 ，以 为圆心， 为半径的圆与以 为直 径的圆相切，求 弦 的长． 图 1 图 2 图 3 O A B C O AOBC = D BC AC OD OAC α∠ = α AOD∠ B AC A D AD O E O AD BC AE 2.（黄浦）已知四边形 ABCD 中，AD∥BC， ，点 E 是射线 AD 上一点，点 F 是射线 DC 上一点，且满足 . （1）如图 8，当点 E 在线段 AD 上时，若 AB=AD，在线段 AB 上截取 AG=AE，联结 GE. 求证：GE=DF； （2）如图 9，当点 E 在线段 AD 的延长线上时，若 AB=3，AD=4， ，设 ， ，求 关于 的函数关系式及其定义域； （3）记 BE 与 CD 交于点 M，在（2）的条件下，若△EMF 与△ABE 相似，求线段 AE 的长. 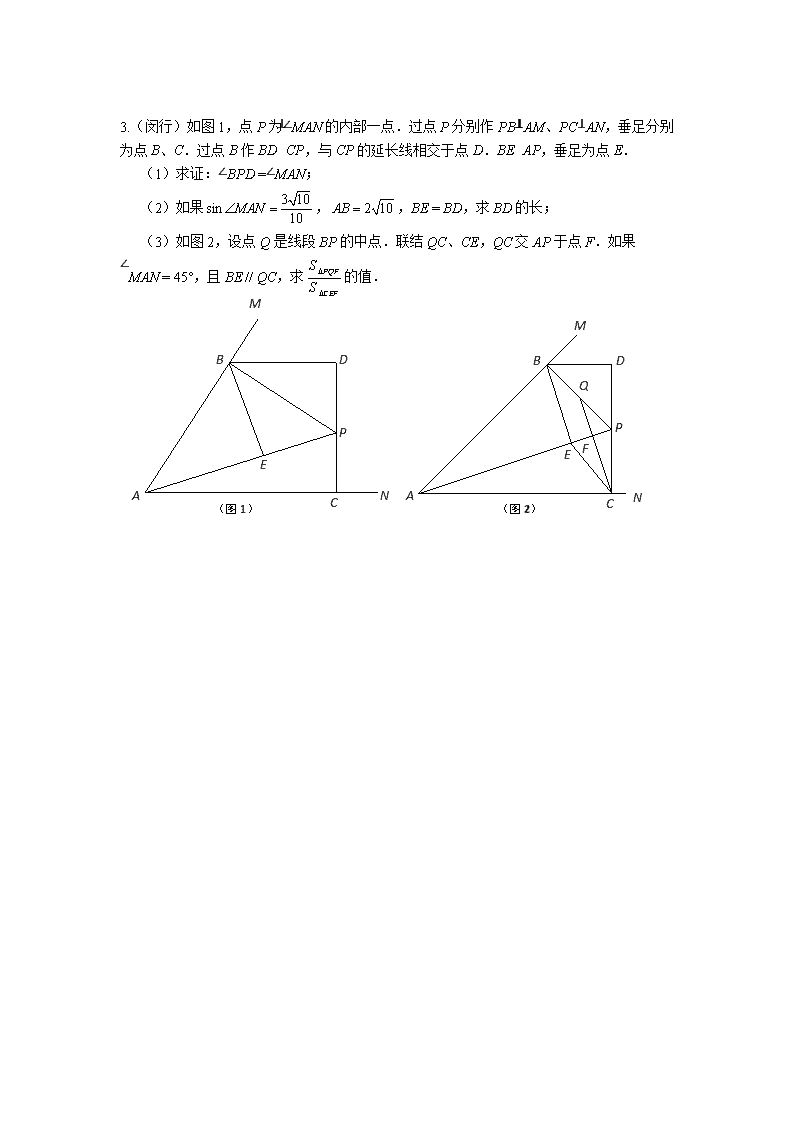2ABC C∠ = ∠ BEF A∠ = ∠ 1cos 3A = AE x= DF y= y x DA B C E F 图 9 A B C E FG D 图 8 3.（闵行）如图 1，点 P 为∠MAN 的内部一点．过点 P 分别作 PB⊥AM、PC⊥AN，垂足分别 为点 B、C．过点 B 作 BD⊥CP，与 CP 的延长线相交于点 D．BE⊥AP，垂足为点 E． （1）求证：∠BPD =∠MAN； （2）如果 ， ，BE = BD，求 BD 的长； （3）如图 2，设点 Q 是线段 BP 的中点．联结 QC、CE，QC 交 AP 于点 F．如果 ∠MAN = 45°，且 BE // QC，求 的值． 3 10sin 10MAN∠ = 2 10AB = PQF CEF S S ∆ ∆ E M （图 2） A N Q F P C DB M NA B C D P （图 1） E A B C D E 备用图 4.（金山）如图，在 中， ， cm， cm，动点 由点 向点 以每秒 速度在边 上运动，动点 由点 向点 以每秒 速度在边 上运动，若点 ，点 从点 同时出发，运动 秒( )，联结 . （1）求证： ∽ ． （2）设经过点 、 、 三点的圆为⊙ . ①当⊙ 与边 相切时，求 的值. ②在点 、点 运动过程中，若⊙ 与边 交于点 、 （点 在点 左侧）， 联结 并延长 交边 于点 ，当 与 相似时，求 的值. ABCRt∆ 90=∠C 16=AC 20=AB D C A cm1 AC E C B cm3 4 BC D E C t 0>t DE DCE∆ BCA∆ D C E P P AB t D E P AB F G F G CP CP AB M PFM∆ CDE∆ t A B C D E P E O B A CM H O B A CD P F 5.（宝山）如图已知： AB 是圆 O 的直径，AB=10，点 C 为圆 O 上异于点 A、B 的一点， 点 M 为弦 BC 的中点． （1）如果 AM 交 OC 于点 E，求 OE：CE 的值； （2）如果 AM⊥OC 于点 E，求∠ABC 的正弦值； （3）如果 AB：BC=5：4，D 为 BC 上一动点，过 D 作 DF⊥OC，交 OC 于点 H，与射线 BO 交于圆内点 F，请完成下列探究． 探究一：设 BD=x，FO=y，求 y 关于 x 的函数解析式及其定义域． 探究二：如果点 D 在以 O 为圆心，OF 为半径的圆上，写出此时 BD 的长度． 6.（静安）已知，如图，梯形 中， ∥ ， ， ，动点 在射线 上，以 为半径的 交边 于点 （点 与点 不重合），联结 、 ，设 ， . （1）求证： ∥ ； （2）求 关于 的函数解析式，并写出定义域； （3）联结 ，当 时，以 为圆心半径为 的 与 相交，求 的取值 范围. ABCD AD BC 2AD = 6AB BC CD= = = P BA BP P BC E E C PE PC BP x= PC y= PE DC y x PD PDC B∠ = ∠ D R D P R 7.（徐汇）如图，在△ 中， ， ，点 是 边上一动点（不 与点 、 重合），以 长为半径的 与边 的另一个交点为 ，过点 作 于点 . （1）当 与边 相切时，求 的半径； （2）联结 交 于点 ，设 的长为 ， 的长为 ，求 关于 的函数解析式， 并直接写出 的取值范围； （3）在（2）的条件下，当以 长为直径的 与 相交于 边上的点 时，求相交 所得的公共弦的长. ABC 10AC BC= = 3cos 5C = P AC A C PA P AB D D DE CB⊥ E P BC P BP DE F AP x PF y y x x PE Q P AC G 8.（奉贤）如图，已知△ ， ， ，点 在边 上，联结 ，以点 为圆心， 为半径画圆，与边 交于点 ，点 在圆 上，且 . （1）设 为 ，点 、 之间的距离为 ，求 关于 的函数解析式，并写出定义域； （2）如果 是弧 中点，求 的值； （3）联结 ，如果四边形 是梯形，求 的长. ABC 2AB = 45B∠ = ° D BC AD A AD AC E F A AF AD⊥ BD x D F y y x E DF :BD CD CF ADCF BD 9.（崇明）如图，在梯形 中， ∥ ， ， ， ，点 为 边上一点，且 ，点 是 边上的一个动点（与点 、点 不重合），点 在射线 上，且 ，设 的长为 ， 的长为 . （1）当点 在线段 上时，求 与 之间的函数关系式，并写出自变量 的取值范围； （2）当以点 为圆心， 长为半径的 与以点 为圆心， 长为半径的 相切时， 求线段 的长； （3）当△ 为等腰三角形时，直接写出线段 的长. ABCD AD BC 8AB DC= = 12BC = 3cos 5C = E AB 2BE = F BC B C G CD EFG B∠ = ∠ BF x CG y G DC y x x B BF B C CG C BF CFG BF 10.（普陀）如图 12，在 Rt 中，∠ACB=90°，AB=5， ，点 O 是边 AC 上一个动点（不与 A、C 重合），以点 O 为圆心，AO 为半径作 ， 与射线 AB 交于点 D；以点 C 为圆心，CD 为半径作 ，设 . （1）如图 13，当点 D 与点 B 重合时，求 的值； （2）当点 D 在线段 AB 上，如果 与 AB 的另一个交点 E 在线段 AD 上时，设 AE=y， 试求 y 与 之间的函数解析式，并写出 的取值范围； （3）在点 O 的运动的过程中，如果 与线段 AB 只有一个公共点，请直接写出 的取值 范围. ABC 4cos 5BAC∠ = O O C OA x= x C x x C x 11.（松江）如图，已知 Rt△ABC 中，∠ACB=90°，AC= ，BC=16．点 O 在边 BC 上， 以 O 为圆心，OB 为半径的弧经过点 A．P 是弧 AB 上的一个动点． （1）求半径 OB 的长； （2）如果点 P 是弧 AB 的中点，联结 PC，求∠PCB 的正切值； （3）如果 BA 平分∠PBC，延长 BP、CA 交于点 D，求线段 DP 的长． 24 · （第 25 题图） O BC A · （备用图） O BC A 12.（长宁）如图，在 中， ， ，点 在边 上（点 与点 不重合），以点 为圆心， 为半径作 交边 于另一点 ， ， 交边 于点 ； （1）求证： ； （2）若 ， ，求 关于 的函数关系式并写出定义域； （3）延长 交 延长线于点 ，联结 ，若 与 相似，求线段 的长. E D C A B P C A B C A B Rt ABC 90ACB∠ =  3AC = 4BC = P AC P A P PA P AB D ED DP⊥ BC E BE DE= BE x= AD y= y x ED CA F BP BDP DAF AD