2017年度中考数学（直线与圆的位置关系）押轴题专练2 20页

‎ 直线与圆的位置关系 ‎1、在平面直角坐标系xOy中以点（-3,4）为圆心，4为半径的圆（ ）‎ A、与x轴相交，与y轴相切 B、与x轴相离，与y轴相交 C、与x轴相切，与y轴相交 D、与x轴相切，与y轴相离 ‎【解题思路】由圆心的坐标为（-3,4）知圆心到x轴的距离为4，与y轴的距离为3，又圆的半径为4，由直线和圆的位置关系可知： 圆与x轴相切，与y轴相交。故选C.‎ ‎【答案】C ‎【点评】本题主要考查直线与圆的位置关系。判断直线与圆的位置关系有两种方法：1、直线与圆的交点个数；2、圆的圆心到直线的距离与圆的半径之间的大小关系。难度较小 ‎2．）如图，A、B、C、D是⊙O上的四个点，AB=AC，AD交BC于点E，AE=3，ED=4，则AB的长为 .‎ A B C D E ‎·‎ O ‎【解题思路】根据相等的弦所对的劣弧（或优弧）相等，相等的弧所对的圆周角相等，所以∠ABE=∠D，又因为∠BAE=∠DAB，所以△BAE≌△DAB，所以，即AB2=AD•AE=3×（3+4）=21,所以AB=。‎ ‎【答案】‎ ‎【点评】本题主要考查圆的性质、相似三角形的判定与性质，解题关键是找相似三角形。难度中等。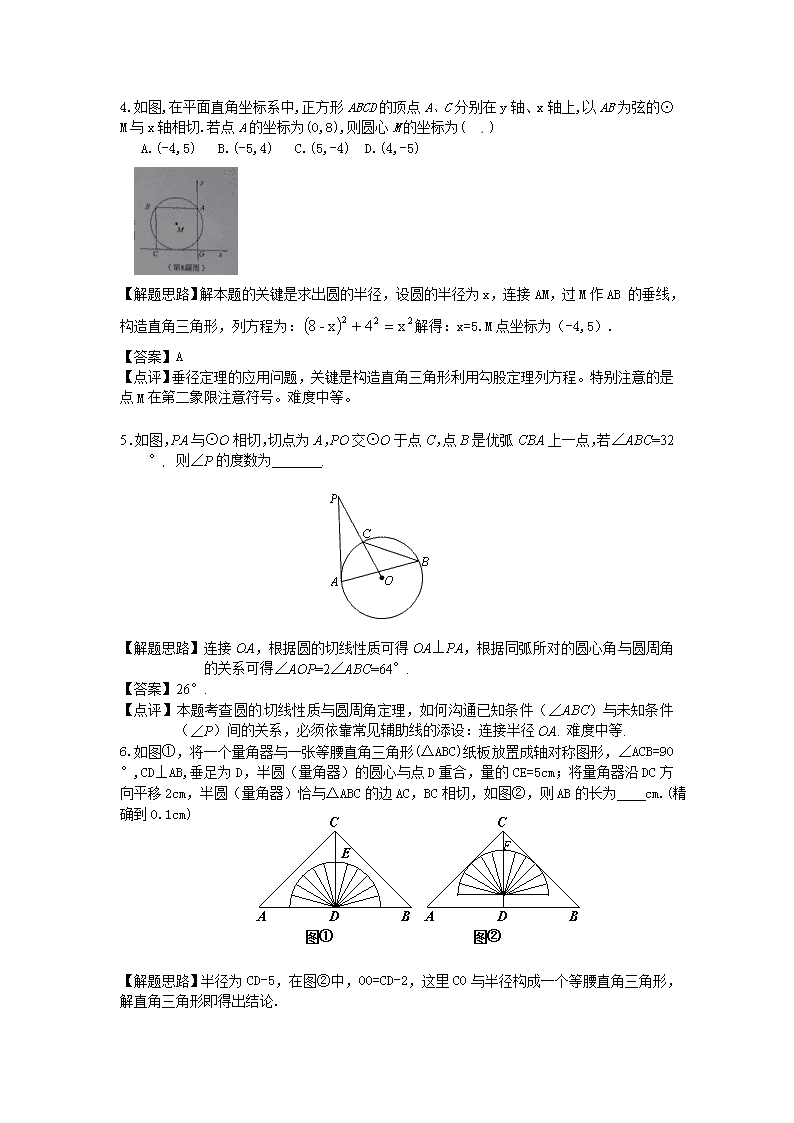‎ ‎3．如图，PA、PB是⊙O的切线，AC是⊙O的直径，∠P=50°，则∠BOC的度数为 A．50° B．25° ‎ C．40° D．60°‎ ‎【解题思路】由PA、PB是⊙O的切线，根据切线的性质得到∠OAP=∠OBP=90°，再根据四边形的内角和为360°可得到∠AOB，而AC是⊙O的直径，根据互补即可得到∠BOC的度数．‎ ‎【答案】∵PA、PB是⊙O的切线，‎ ‎∴∠OAP=∠OBP=90°，‎ 而∠P=50°，‎ ‎∴∠AOB=360°-90°-90°-50°=130°，‎ 又∵AC是⊙O的直径，‎ ‎∴∠BOC=180°-130°=50°．‎ 故选A ‎【点评】本题考查了圆的切线的性质：圆的切线垂直于过切点的半径；也考查了四边形的内角和为360°．难度中等．‎ ‎4.如图,在平面直角坐标系中,正方形ABCD的顶点A、C分别在y轴、x轴上,以AB为弦的⊙M与x轴相切.若点A的坐标为(0,8),则圆心M的坐标为( )‎ A.(-4,5) B.(-5,4) C.(5,-4) D.(4,-5)‎ ‎【解题思路】解本题的关键是求出圆的半径，设圆的半径为x，连接AM，过M作AB 的垂线，构造直角三角形，列方程为：解得：x=5.M点坐标为（-4,5）.‎ ‎【答案】A ‎【点评】垂径定理的应用问题，关键是构造直角三角形利用勾股定理列方程。特别注意的是点M在第二象限注意符号。难度中等。‎ ‎5．如图，PA与⊙O相切，切点为A，PO交⊙O于点C，点B是优弧CBA上一点，若∠ABC=32°， 则∠P的度数为 .‎ ‎【解题思路】连接OA，根据圆的切线性质可得OA⊥PA，根据同弧所对的圆心角与圆周角的关系可得∠AOP=2∠ABC=64°.‎ ‎【答案】26°.‎ ‎【点评】本题考查圆的切线性质与圆周角定理，如何沟通已知条件（∠ABC）与未知条件（∠P）间的关系，必须依靠常见辅助线的添设：连接半径OA. 难度中等.‎ C C A B E D A B F D 图①‎ 图②‎ ‎6.如图①，将一个量角器与一张等腰直角三角形(△ABC)纸板放置成轴对称图形，∠ACB=90°,CD⊥AB,垂足为D，半圆（量角器）的圆心与点D重合，量的CE=‎5cm；将量角器沿DC方向平移‎2cm，半圆（量角器）恰与△ABC的边AC，BC相切，如图②，则AB的长为 cm.(精确到‎0.1cm)‎ ‎【解题思路】半径为CD-5，在图②中，OO=CD-2，这里CO与半径构成一个等腰直角三角形，解直角三角形即得出结论.‎ ‎【答案】24.5.‎ ‎【点评】本题考察了切线的性质，平移的知识及解直角三角形. 半径为CD-5，在图②中，OO=CD-2，这里CO与半径构成一个等腰直角三角形，则2（CD-5）2=（CD-2）2，解得CD≈12.25，∴AB=‎24.5厘米.‎ ‎7．已知AC⊥BC于C，BC=a，CA=b，AB=c，下列选项中⊙O的半径为的是 ‎ ‎ ‎【解题思路】由图A可以知道△ABC的内切圆是圆O,所以设各边的切点为D 、E、 F，根据题意得：AE=AF,BF=BD,CD=CE,且四边形CDEO为正方形，所以设半径为x，则有CD=CE=x，根据题意得：b-x+a-x=c，解得：；不可选；对于B选项，可以断定△ADO∽△ABC，所以,所以，解得：，答案不可选。由C答案可得：‎ 四边形ODCE为正方形。根据△AEO∽△ABC，得：,所以，解得：‎ X=，所以答案选C。‎ ‎【答案】C ‎【点评】本题考查了三角形的相似的实际应用，以及三角形内切圆的性质的综合应用，题目难度较大。‎ ‎ 8.如图，PA,PB是⊙O是切线，A,B为切点， AC是⊙O的直径，若∠BAC=250，则∠P= __________度。‎ ‎【解题思路】连结OP，由切线长定理，切线性质，及三角形性质可得：‎ ‎【答案】50‎ ‎【点评】利用切线的性质时，常连结圆心与切点。从圆外一点引圆的两条切线时应考虑到圆切线长定理。‎ ‎9如图，在Rt△ABC中，∠C=90°，∠A=60°，BC=‎4cm，以点C为圆心，以‎3cm长为半径作圆，则⊙C与AB的位置关系是 。‎ 第13题 A C B ‎【解题思路】要确定⊙C与AB的位置，只要比较圆心C到 AB的距离与圆的半径的大小。过C作CD⊥AB，垂足为D，‎ 得Rt△BCD，∠A+∠B=90°知∠B=30°，有三角函数或30°‎ 角所对直角边等于斜边的一半，得CD=BC=2<半径3，故相交。‎ ‎【答案】相交 ‎【点评】考查圆与直线的位置关系只需比较圆心到直线的距离与圆半径的大小。C到AB的距离CD是直角三角形的边，解三角形可得CD长度。难度中等。‎ ‎10．如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C．若∠A=40º，则∠C=_____．‎ 题9图 B C O A ‎【解题思路】连接OB，由AB与⊙O相切知：OB⊥AB，所以∠AOB=90º-∠A=50º，再根据圆半径相等可得∠C=∠OBC，利用外角性质得：∠AOB=∠OBC+∠C，即∠C=25º.‎ ‎【答案】25º ‎【点评】过切点连半径是在直线与圆相切中常见的辅助线．通过作出辅助线，构造直角三角形，从而解决问题．难度中等 第23题图 ‎11．(本题满分8分) （2011山东枣庄，23,8分）如图，点在的直径的延长线上，点在上，且AC=CD，∠ACD=120°.‎ ‎（1）求证：是的切线；‎ ‎（2）若的半径为2，求图中阴影部分的面积.‎ ‎【解题思路】要证明是的切线，只要连半径，证明垂直即可，要计算阴影部分的面积，借助间接计算即可得到．‎ ‎【答案】（1）证明：连结.‎ ‎∵ ，，‎ ‎∴ .∵ ,∴ . ‎ ‎∴ . ∴ 是的切线. ‎ ‎（2）解:∵∠A=30o, ∴ . ∴π. 在Rt△OCD中,. ∴.∴ 图中阴影部分的面积为π. ‎ ‎【点评】本题是一道简单的综合题，综合了圆的基本性质，直线与圆的位置关系及三角函数，圆的基本性质很多，要从弧，弦，角等方面着手进行分析与突破．同时考查了同学们的分析、推理论证与综合运算能力，难度中等．‎ ‎12.如图，AB是⊙O的直径，AC是弦，CD是⊙O的切线，C为切点，AD⊥CD于点D．‎ 求证：（1）∠AOC=2∠ACD；‎ ‎（2）AC2＝AB·AD．‎ ‎【解题思路】21．(本题满分9分)‎ 证明：（1）∵CD是⊙O的切线，∴∠OCD=90°， ‎ 即∠ACD+∠ACO=90°．…① …………………………………………2分 ‎∵OC=OA，∴∠ACO=∠CAO，‎ ‎∴∠AOC=180°-2∠ACO，即∠AOC+∠ACO=90°. …②……………4分 由①，②，得：∠ACD-∠AOC=0，即∠AOC=2∠ACD；………………5分 ‎（2）如图，连接BC．‎ ‎∵AB是直径，∴∠ACB=90°．……………6分 在Rt△ACD与△RtACD中，‎ ‎∵∠AOC=2∠B，∴∠B=∠ACD，‎ ‎∴△ACD∽△ABC，………………………8分 ‎∴，即AC2=AB·AD． ………9分 ‎【答案】‎ ‎【点评】直线和圆的位置关系及可以单独命题，又可以与函数、三角形函数、相似等知识进行综合，要善于将各个部分综合起来，充分利用数形结合的思想进行解题．同时本题也是一道动态存在探究题，要求考生具有较强观察能力、分析能力和归纳能力，是道不可多得的好题，有利于培养学生的思维能力，但难度较大，具有明显的区分度．‎ ‎13（山东 济宁）A 第20题 N C B D E F M O O 20、（7分）如图，AB是⊙O的直径，AM和BN是它的两条切线，DE切⊙‎ O于点E，交AM与于点D，交BN于点C，F是CD的中点，连接OF。‎ ‎（1） 求证：OD∥BE;‎ ‎(2) 猜想：OF与CD有何数量关系？并说明理由。‎ ‎【解题思路】（1）要证明OD∥BE，只需知道∠AOD=∠ABE；∠ABE是弧AE所对的圆周角等于弧AE所对圆心角度数的一半；DE是切线，连接常见的辅助线OE（过切点的半径），此时问题转化为证明∠AOD=∠AOE，由图可知证明∠AOD=∠EOD即可，由于AM、DE是⊙O的切线，所以有Rt△ADO和Rt△EDO并且∠ADO=∠EDO，因而得∠AOD=∠EOD=∠AOE，从而得证。‎ ‎（2）因为AD和DE、CE和CB都是圆的公切线，所以有∠ADO=∠EDO ∠OCB=∠OCE，由AM∥BN得，∠ADO+∠EDO+∠OCB+∠OCE=180°所以∠EDO+∠OCE=90°，△DOC为Rt△，因为F是CD的中点，所以直角三角形斜边上的中线等于斜边的一半OF =CD。‎ ‎【答案】解：（1）证明：连接OE ‎∵AM、DE是⊙O的切线，OA、OE是⊙O的半径 ‎∴∠ADO=∠EDO,∠DAO=∠DEO=90°…………1分 ‎∴∠AOD=∠EOD=∠AOE …………2分 A 第20题 N C B D E F M O O ‎∵∠ABE=∠AOE ∴∠AOD=∠ABE ∴OD∥BE …………3分 ‎(2) OF =CD …………4分 理由：连接OC ‎∵BE、CE是⊙O的切线 ‎∴∠OCB=∠OCE …………5分 ‎∵AM∥BN ‎∴∠ADO+∠EDO+∠OCB+∠OCE=180°‎ 由（1）得 ∠ADO=∠EDO ‎∴2∠EDO+2∠OCE=180° 即∠EDO+∠OCE=90° …………6分 在Rt△DOC中， ∵ F是DC的中点 ∴OF =CD …………7分 ‎【点评】此题考查远的相关性质。遇到切线问题常要用到过切点的半径，也是常作的辅助线；证明两线段平行，通过同位角来证明，本题中的同位角一个是圆周角，一个是圆心角的一部分，结合圆的有关性质可以得证。（2）此问主要应用了公切线性质中的平分所成的角，结合远的性质得出证明。此题综合考查了学生掌握圆的有关性质和分析问题的能力！难度中等。‎ ‎14.如图，BD为⊙O的直径，AB=AC,AD交BC于点E,AE=2，ED=4,‎ ‎(1)求证:△ABE∽△ADB;‎ ‎(2)求AB的长；‎ ‎(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系，并说明理由. ‎ ‎（第18题图）‎ ‎【解题思路】（1）由AB=AC可得∠ABC=∠D，又∠BAD=90°，所以相似；(2)由相似可知，，，AB=；（3）连接OA，证可得直线FA与⊙O相切。‎ ‎【答案】(1)证明:∵AB=AC,∴∠ABC=∠C,∵∠C=∠D,∴∠ABC=∠D,又∵∠BAE=∠EAB,∴△ABE∽△ADB；(2)∵△ABE∽△ADB,∴，∴AB=. （3）直线FA与⊙O相切，理由如下：连接OA，∵BD为⊙O的直径，∴∠BAD=90°，∴，BF=BO=,∵AB=,∴∴直线FA与⊙O相切。‎ ‎【点评】充分借助圆中一些特殊的性质来证明几何问题。难度较大。‎ ‎ ‎ ‎15（山东临沂 第23题 9分）如图以O为圆心的圆与△AOB的边AB相切于点C，与OB相较于点D,且OD=BD,已知sinA=,AC=.‎ ‎（1）求⊙O的半径；‎ ‎（2）求图中阴影部分的面积.‎ 解题思路：（1）已知圆的切线的题目通常都是连接圆心与切点，根据切线的性质能得到直角三角形，从而运用解直角三角形和勾股定理来求圆的半径；（2）求不规则的阴影部分的面积可以把它转化为直角三角形OBC的面积与扇形OCD面积的差.‎ 解答：（1）连接OC,‎ ‎∵⊙O与边AB相切于点C，∴OC⊥AB,‎ O A C B D ‎∵sinA==,∴设OC=2x,则OA=5x,‎ 由勾股定理得：（5x）2=(2x)2+()2‎ 解得x=1, ∴⊙O的半径是2.‎ ‎（2）∵OC⊥AB,OC=OD=BD, ∴∠B=300,‎ ‎∴∠BOC=600,OB=4.‎ 由勾股定理得：BC=,‎ ‎∴S阴影=S△BOC-S扇形=.‎ 点评：本题主要考查了圆的切线的性质、解直角三角形、勾股定理、直角三角形性质以及扇形的面积公式.利用面积的和差把不规则的图形的面积转化为规则图形的面积是一种常用的方法.本题难度中等.‎ ‎23．本题共8）如图，是半圆的直径，点是圆心，点是的中点，交半圆于点。点是的中点，连接，过点作∥交的延长线于点。‎ ‎23题图 ‎（1）求的度数；‎ ‎（2）求证：是半圆的切线．‎ ‎【解题思路】（1）在中，‎ 显然,故可得到。‎ ‎（2）由（1）知，则。‎ 由∥，得，所以，即可证明是半圆的切线．‎ ‎【答案】（1）解：∵点是的中点，‎ ‎∴,∵,∴,‎ ‎∵,∴.‎ ‎∴在中，‎ 显然,∴.‎ ‎(2)证明：∵，∴。‎ ‎∵点是的中点，∴.‎ ‎∵∥，∴，∴.‎ 即.∴是半圆的切线． ‎ ‎【点评】 本题把特殊角的三角函数与圆的有关知识结合在一起，考查了圆周角和圆心角的关系，平行线的性质以及切线的证明。具有一点的综合性，题目难度中等。‎ ‎16.（本小题满分8分）‎ ‎（2011山东滨州，22，8分）如图，直线PM切⊙O于点M,直线PO交⊙O于A、B两点，弦AC∥PM, 连接OM、BC.‎ 求证：（1）△ABC∽△POM;‎ ‎(2).‎ ‎【解题思路】第一问是证明两个三角形相似，两个三角形对应角相等，对应边成比例的两个三角形叫做相似三角形。证明的方法：1.平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似2.如果一个三角形的两个角与另一个三角形的两个角对应相等, 那么这两个三角形相似3.如果两个三角形的两组对应边的比相等,并且相应的夹角相等, 那么这两个三角形相似 4.如果两个三角形的三组对应边的比相等,那么这两个三角形相似对于本题来说用如果一个三角形的两个角与另一个三角形的两个角对应相等, 那么这两个三角形相似最简单。有两个直角∠ACB=∠PMO还有平行可得∠CAB=∠P，可得两个三角形相似。‎ 第二问：需要把等积式转化成比例式，看一下是不是位于两个相似的三角形中，有对应边成比例可得证。‎ ‎【答案】证明：（1）∵直线PM切⊙O于点M，∴∠PMO=90°………………1分 ‎ ∵弦AB是直径，∴∠ACB=90°………………2分 ‎ ∴∠ACB=∠PMO………………3分 ‎ ∵AC∥PM, ∴∠CAB=∠P ………………4分 ‎ ∴△ABC∽△POM………………5分 ‎(2) ∵ △ABC∽△POM, ∴………………6分 ‎ 又AB=2OA,OA=OM, ∴………………7分 ‎∴………………8分 ‎【点评】主要考察三角形相似的判定和比例式的成立情况得证明，要注意方法的选择和问题的转化的能力的锻炼，难度中等。‎ ‎17．如图8所示．P是⊙O外一点．PA是⊙O的切线．A是切点．B是⊙O上一点．且PA=PB，连接AO、BO、AB，并延长BO与切线PA相交于点Q．‎ ‎ （1）求证：PB是⊙O的切线；‎ ‎ （2）求证： AQ·PQ= OQ·BQ； ‎ ‎ （3）设∠AOQ=．若cos=．OQ= 15．求AB的长 ‎ ‎‎_‎ Q ‎_‎ P ‎_‎ O ‎_‎ B ‎_‎ A 图8‎ ‎【解题思路】1）利用切线的定义证明切线 2） 利用相似三角形证明 3） 利用三角函数 ‎【答案】（1）证明：如图，连结OP ‎ ∵PA=PB，AO=BO，PO=PO ‎ ∴△APO≌△BPO ∴∠PBO=∠PAO=90°‎ ‎ ∴PB是⊙O的切线 ‎ （2）证明：∵∠OAQ=∠PBQ=90°‎ ‎ ∴△QPB∽QOA ‎∴ 即AQ·PQ= OQ·BQ ‎ （3）解：cos== ∴AO=12‎ ‎ ∵△QPB∽QOA ∠BPQ=∠AOQ=‎ ‎ ∴tan∠BPQ== ∴PB=36 PO=12‎ ‎ ∵AB·PO= OB·BP ∴AB=‎ ‎_‎ Q ‎_‎ P ‎_‎ O ‎_‎ B ‎_‎ A 图8‎ ‎【点评】本题考察相似三角形，切线的判定即锐角三角函数。‎ ‎19.如图（13），D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD.‎ ‎(1)求证:CD是⊙O的切线;‎ ‎(2)过点B作⊙O的切线交CD的延长线于点E,若BC=6,tan∠CDA=,求BE的长 ‎【解题思路】：(1)连接OD，只要证明OD⊥CE，即可说明CD为切线；‎ ‎（2）根据已知条件可判断△CAD∽△CDB；连接OE，可得：∠CDA=∠BEO,设OB=2x,BE=3x,利用相似得出的比例关系，求出x的值。‎ ‎【答案】（1）证明：连接OD，∴∠CBD=∠BD0，∵线段AB是直径，∴∠ADB=900，∴∠ADO+∠ODB=900，又∵∠CDA=∠CBD，∠CBD=∠BD0，∴∠CDA+∠BD0=900，即∠CDO=900，∴CD是⊙O的切线;‎ ‎(2)∵∠CDA=∠CBD.∠C是公共角，∴△CAD∽△CDB,∴CD2=CA×CB,∴连接OE，BE是⊙O的切线，tan∠CDA=,设OB=2x,BE=3x,∴CD2=6(6-4x)=36-24x,又∵△COD∽△CEB,∴=,即16=36-24x,解得：x=,∴BE=2x=2.5.‎ ‎【点评】本题是一道圆与三角形的综合性题目，解题的关键是借助辅助线构建新的直角三角形，推出角的关系，利用三角形的相似，得出比例关系式，利用三角函数的边角关系，设出边的长度，代入比例式运算求值。本题难度较大。‎ ‎19． (本题满分12分）如图，在梯形ABCD中，AB//CD，∠BAD＝90°，以AD为直径的半圆O与BC相切．‎ ‎(1)求证：OB丄OC；‎ ‎(2)若AD＝12，∠BCD＝60°，⊙O1与半⊙O外切，并与BC、CD相切，求⊙O1的面积．‎ ‎【解题思路】(1)设半圆O与直线BC的切点为F，连接切点与圆心，把∠BOC分成两个角∠FOB和∠FOC，然后由“HL”定理或“SSS”定理证明Rt△AOB≌Rt△FOB，Rt△COD≌Rt△COF，得出∠BOC＝90°．(2)由切线长定理得出∠DCO＝∠BCO＝30°，得出DC＝12．过点O1做O‎1G⊥DC，设O‎1G＝x，由直角三角形的性质得出O‎1C＝2O‎1G＝2x．由两圆的连心线经过切点，得出O‎1C＝6－x，由此构建方程2x＝6－x，解方程求出x的值，然后根据圆的面积公式计算出⊙O1的面积．‎ ‎【答案】（1）方法一：证明：设半圆O与BC切于F，连接OF．‎ ‎∵AD是半圆O的直径，∠BAD＝90°，‎ ‎∴AB与半圆O相切于点A．‎ ‎∵AB//CD，∠BAD＝90°，‎ ‎∴∠ADC＝90°，∴CD于半圆O切于D．‎ ‎∵半圆O与BC切于F，‎ ‎∴OF⊥BC，BA＝BF，FC＝CD．‎ 在Rt△AOB和Rt△FOB中，‎ ‎∴△AOB≌△FOB（HL）．‎ ‎∴∠FOB＝∠AOB．‎ 同理Rt△COD≌Rt△COF，‎ ‎∴∠FOC＝∠DOC．‎ ‎∴∠FOB+∠FOC＝∠AOB+∠DOC．‎ 又∵∠FOB+∠FOC+∠AOB+∠DOC＝180°，‎ ‎∴∠BOC＝∠FOB+∠FOC＝90°，即OB⊥OC．‎ 方法二：证明：设半圆O与BC切于F，连接OF．‎ ‎∵AD是半圆O的直径，∠BAD＝90°，‎ ‎∴AB与半圆O相切于点A．‎ ‎∵AB//CD，∠BAD＝90°，‎ ‎∴∠ADC＝90°，∴CD于半圆O切于D．‎ ‎∵半圆O与BC切于F，‎ ‎∴OF⊥BC，即∠OFB＝∠OFC＝90°．‎ 又∵OA＝OF＝OD，‎ 在Rt△AOB和Rt△FOB中 ‎∴Rt△AOB≌Rt△FOB（HL）‎ ‎∴∠FOB＝∠AOB．‎ 同理Rt△COD≌Rt△COF，‎ ‎∴∠FOC＝∠DOC．‎ ‎∴∠FOB+∠FOC＝∠AOB+∠DOC．‎ 又∵∠FOB+∠FOC+∠AOB+∠DOC＝180°，‎ ‎∴∠BOC＝∠FOB+∠FOC＝90°，即OB⊥OC．‎ ‎(2)过点O1做O‎1G⊥DC．∵CD与⊙O1相切，∴O‎1G是⊙O1的半径．∵∠DOB＝60°，∴∠DCO＝∠BCO＝30°．∵AD＝12，∴OD＝6．∴OC＝12．设O‎1G＝x，∴O‎1C＝2x，又O‎1C＝6－x，∴2x＝6－x，解得x＝2，即⊙O1的半径为2．∴⊙O1的面积为π×22＝4π．‎ ‎【点评】①圆的切线经过半径的外端，且垂直于半径；②过圆心作切线的垂线段，则垂线段等于半径；证明垂直，可以把相交成的角分成两个角，证明这两个角的和等于平角的一半，即可得证．‎ ‎21．如图，在 Rt△ABC中,∠ACB＝90D是AB 边上的一点，以BD为直径的 ⊙0与边 AC 相切于点E，连结DE并延长，与BC的延长线交于点 F . ‎ ‎( 1 ）求证： BD = BF ;‎ ‎( 2 ）若 BC = 12 , AD = 8 ，求 BF 的长．‎ ‎ ‎ ‎【解题思路】(1)连接OE.‎ ‎∵AC切⊙0于点E ‎∴OE⊥AC 则∠AEO=‎ ‎∵∠ACB＝90‎ ‎∴∠AEO=∠ACB ‎∴OE∥BF ‎∴∠OED=∠F ‎∵OE=OD ‎∴∠ODE=∠OED ‎∴∠F=∠ODE ‎∴BD = BF ‎(2)由（1）得：设BF = BD等于2‎ ‎ ∵OE∥BF ‎ ‎ ∴△AOE∽△ABC ‎ ∴即 ‎ 解得： ‎ ‎∴BF 的长为8.‎ ‎【答案】(2)8‎ ‎【点评】本题主要考查了切线的性质、等角对等边、三角形相似的判定及其性质的运用，比较综合的运用了初中数学知识解决数学问题，难度中等.‎ ‎22．如图，在锐角△ABC中，AC是最短边；以AC中点O为圆心，AC长为半径作⊙O，交BC于E，过O作OD∥BC交⊙O于D，连结AE、AD、DC．‎ ‎（1）求证：D是的中点；‎ ‎（2）求证：∠DAO =∠B +∠BAD；‎ ‎（3）若，且AC=4，求CF的长.‎ ‎【解题思路】（1）证明弧的中点可用垂径定理，也可用同圆中两圆心角、两弧、两弦、两弦心距中有一组量相等，其余各组量也对应相等。（2）可用三角形的外角等于与它不相邻的两个内角的和来证，延长AD交BC于点即把∠DAO转化成∠ADO再转化成∠AHC，或者延长OD交AB于点G把∠DAO转化成∠ADO、把∠B转化成∠AGD。（3）有关三角形面积面积比的计算一般转化为两三角形相似，用面积比＝相似比的平方。‎ ‎【答案】证明：（1）方法一：‎ ‎∵AC是⊙O的直径 ‎∴AE⊥BC …………1分 ‎∵OD∥BC ‎∴AE⊥OD …………2分 ‎∴D是的中点 …………3分 方法二：‎ 连结OE，‎ ‎∵OD∥BC ‎ ‎∴∠AOD＝∠OCE，∠DOE＝∠OEC ……1分 又∵OE＝OC ‎∴∠OEC＝∠OCE∴‎ ‎∴∠AOD＝∠DOE …………2分 ‎∴D是的中点 …………3分 ‎（2）方法一：‎ 如图，延长OD交AB于G，则OG∥BC …4分 ‎∴∠AGD=∠B ‎∵∠ADO=∠BAD+∠AGD …………5分 又∵OA=OD ‎∴∠DAO=∠ADO ‎∴∠DAO=∠B +∠BAD …………6分 方法二：‎ 如图，延长AD交BC于H …4分 则∠ADO=∠AHC ‎∵∠AHC=∠B +∠BAD …………5分 ‎∴∠ADO =∠B +∠BAD ‎ 又∵OA=OD ‎∴∠DAO=∠B +∠BAD …………6分 ‎（3） ∵AO=OC ∴‎ ‎∵ ∴ …………7分 ‎∵∠ACD=∠FCE ∠ADC=∠FEC=90°‎ ‎∴△ACD∽△FCE …………………8分 ‎∴ 即: …………9分 ‎∴CF=2 …………10分 ‎【点评】本题考查了弧中点的证明，方法有：垂径定理的应用，也可用同圆中两圆心角、两弧、两弦、两弦心距中有一组量相等，其余各组量也对应相等，还考查了平行线的性质，三角形外角的性质，相似三角形中的面积比与相似比的关系等，难度中等．‎ ‎23．已知AB与⊙O相切于点C，OA=OB，OA、OB与⊙O分别交于点D、E。‎ ‎ （Ⅰ）如图，若⊙O的直径为8，AB=10，求OA的长（结果保留根号）；‎ ‎ （Ⅱ）如图‚，连接CD、CE，若四边形ODCE为菱形，求的值。‎ ‎【解题思路】：‎ ‎【答案】：（Ⅰ）如图，连接OC，则OC=4，‎ ‎∵AB与⊙O相切于点C， ∴OC⊥AB，‎ 在△AOB中，由OA=OB，AB=10，得AC=AB=5；‎ 在Rt△AOC中，由勾股定理得OA=；‎ ‎ （Ⅱ）如图‚，连接OC，则OC=OD，‎ ‎∵四边形ODCE为菱形， ∴OD=DC， ∴△ODC是等边三角形，‎ 有∠AOC=60°，由（Ⅰ）知∠OCA=90°，‎ ‎∴∠A=30°， ∴OC=OA，即=。‎ ‎【点评】：本题综合考察了平面几何中的一些主要知识点：切线的性质，勾股定理，菱形的性质，正三角形的判定等，以及识图、推理论证能力。难度中等。‎ ‎24如图，已知⊙O的弦AB垂直于直径CD，垂足为F，点E在AB上，且EA=EC延长EC到点P，连接PB，使PB=PE ‎（1）在以下5个结论中：一定成立的是______________(只需将结论的代号填入题中的横线上) ①弧AC=弧BC; ②OF=CF ③BF=AF;④AC=AE*AB ⑤PB是⊙O的切线。‎ ‎（2）若⊙O的半径为‎8cm,AE:EF=2:1求弓形ACB的面积 ‎【解题思路】本题牵涉到垂径定理，等腰三角形解直角三角形，扇形弓形的相关知识，本题综合性强。‎ 答案：（1）①③④⑤‎ ‎（2）由AE∶EF=2∶1，又CE=EA，∴∠FCE=30º∴∠A=30º。则CF=FO。‎ 连接OB，OA则∠AOB=120º，AB=8‎ ‎∴S=－8×4=－16‎ ‎【点评】本题所涉及的知识较为全面，难度较大。‎ ‎25．如图，已知⊙O的直径AB与弦CD互相垂直，垂足为点E. ⊙O的切线BF与弦AD的延长线相交于点F，且AD=3，cos∠BCD= .‎ ‎（1）求证：CD∥BF；‎ ‎（2）求⊙O的半径；‎ ‎（3）求弦CD的长. ‎ 邹兴平 第21题 ‎【解题思路】根据切线性质和AB⊥CD，可得到CD∥BF；只要求出直径即可求出半径的长，根据同弧所对的圆周角相等，则∠BCD=∠BAD，AB是直径，连接BD，在Rt△ABD中，可根据余弦值及AD的长，求出AB的长度，又AB⊥CD，在Rt△AED中，再次根据余弦值，求出AE的长，根据勾股定理求出ED的长，又根据垂径定理得到CD的长.‎ ‎【答案】解：（1）∵BF是⊙O的切线， ∴AB⊥BF ，∵AB⊥CD ，∴CD∥BF.‎ ‎（2）连结BD ，∵AB是直径 ∴∠ADB=90° ， ∵∠BCD=∠BAD ， ‎ cos∠BCD=，∴cos∠BAD=，又∵AD=3，∴AB=4，∴⊙O的半径为2 .‎ 邹兴平 第21题 F A D E O C B ‎（3）∵cos∠DAE=, AD=3∴AE= , ∴ED= . ‎ ‎ ∴CD=2ED=.‎ ‎ 【点评】本题是关于圆和三角函数的综合体，解题的关键是利用同弧所对的圆周角相等，将问题转化到直角三角形中，根据三角函数的意义来解答问题.难度中等.‎ ‎26．如图，△ABC中，以BC为直径的圆交AB于点D，∠ACD=∠ABC．‎ ‎（1）求证：CA是圆的切线；‎ ‎（2）若点E是BC上一点，已知BE=6，tan∠ABC=，tan∠AEC=，求圆的直径．‎ ‎【解题思路】判定圆的切线就是证明直线垂直于经过切点的半径，求圆的直径时可以利用两个一般角的正切值和线段BE的长，分别表示出AC的长，然后求得BC的长即可。‎ ‎【答案】（1）证明：∵BC为直径，∴∠BDC=90°，∴∠ABC+∠DCB=90°，‎ ‎∵∠ACD=∠ABC，∴∠ACD+∠DCB=90°，∴BC⊥CA,∴CA是圆的切线。‎ ‎（2）在Rt△AEC中，tan∠AEC=,∴,EC=AC,‎ 在Rt△ABC中，tan∠ABC=,∴,BC=‎ ‎∵BC-EC=BE,BE=6,∴-AC=6,‎ 解得：AC= ，‎ ‎∴BC==10，即圆的直径为10.‎ ‎【点评】本题考查了圆的综合知识，将圆的知识和中学学过的其他的有关的几何知识结合在一起考查是此类题目考查的重点，要求学生们具有扎实的基本功，最近几年的中考题的难度也在不断的降低。难度中等。‎ ‎27、如图，射线PG平分EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与EPF的两边相交于A、B和C、D，连结OA，此时有OA∥PE。‎ （1） 求证：AP=AO；‎ （2） 若弦AB=12，求的值；‎ （3） 若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为________，能构成等腰梯形的四个点为___或_____或____.‎ ‎【解题思路】由角平分线加平行线，必然会产生等腰三角形，这是几何中的重要性质，证明方法通过内错角相等，和平分线角相等传递而来；求的值，需要构造直角三角形，过O点作弦AB的垂线就可以；由垂径定理能来求AH，从而求OH。第三小题求菱形，和梯形可以，过O点作CD的垂线，垂足为I，易知OI等于OH，所以有∠DCO=∠OAH=∠CPA，所以OC∥PB，接下来就易证是菱形，和梯形了。‎ ‎【答案】 （1）证明：∵PG平分EPF ∴∠CPO=∠APO 又∵有OA∥PE ∴ ∠CPO= ∠AOP（等量交换）‎ ‎∴∠APO=∠AOP ∴ AP=AO （等角对等边）‎ ‎2）如图，过O点作弦AB的垂线，垂足为H，‎ ‎∵O为圆O的圆心，OH⊥AB，∴ AH=HB=6 ‎ ‎∴由勾股定理得OH==8‎ 又 PH=PA+AH=AO+AH=10+6=16‎ ‎ 在Rt△OPH中， =‎ ‎3）能构成菱形的是P，A，O，C ‎ 能构成等腰梯形是P，B，O，C 或者 P，A，O，D 或者 A，C，D，B。‎ ‎【点评】本题从角平分线出发，引入平行线，又涉及到了垂径定理，从而来证明菱形和梯形 考察知识全面较多，实是一个不可多得的好题。‎