2009青岛中考数学试题 13页

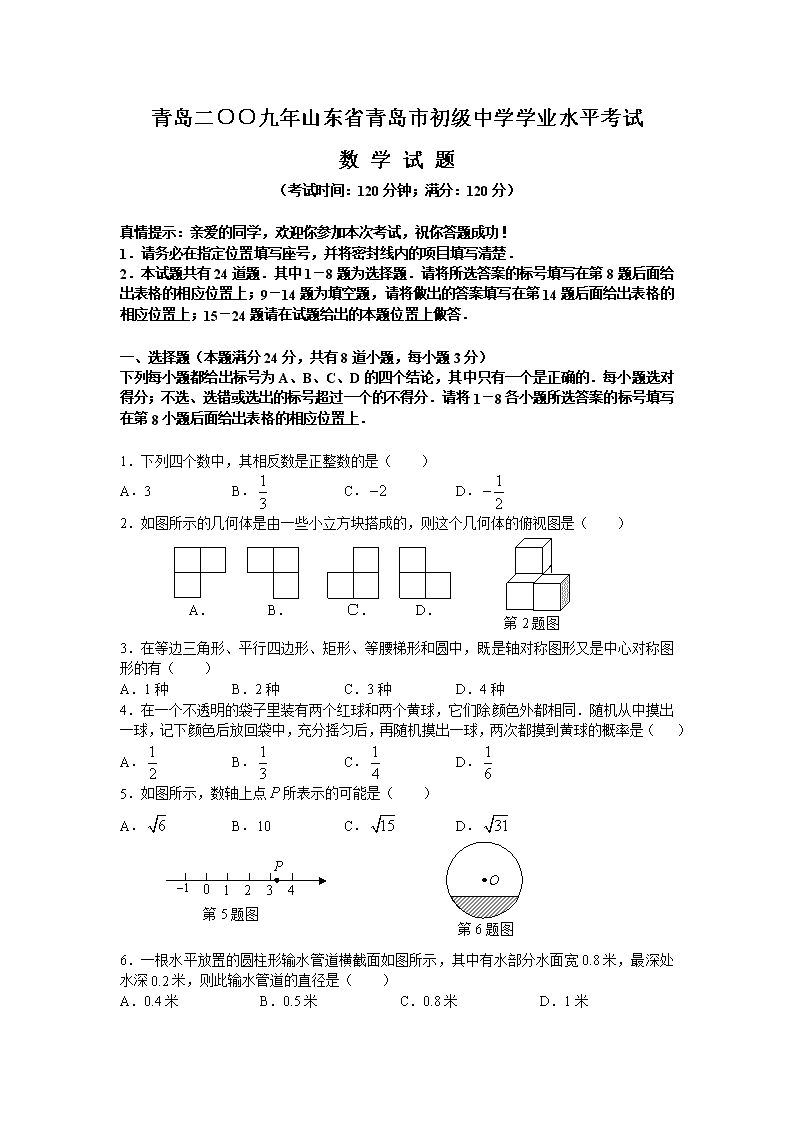
青岛二○○九年山东省青岛市初级中学学业水平考试 数 学 试 题 ‎（考试时间：120分钟；满分：120分）‎ 真情提示：亲爱的同学，欢迎你参加本次考试，祝你答题成功！‎ ‎1．请务必在指定位置填写座号，并将密封线内的项目填写清楚．‎ ‎2．本试题共有24道题．其中1－8题为选择题．请将所选答案的标号填写在第8题后面给出表格的相应位置上；9－14题为填空题，请将做出的答案填写在第14题后面给出表格的相应位置上；15－24题请在试题给出的本题位置上做答．‎ 一、选择题（本题满分24分，共有8道小题，每小题3分）‎ 下列每小题都给出标号为A、B、C、D的四个结论，其中只有一个是正确的．每小题选对得分；不选、选错或选出的标号超过一个的不得分．请将1－8各小题所选答案的标号填写在第8小题后面给出表格的相应位置上．‎ ‎1．下列四个数中，其相反数是正整数的是（ ）‎ A．3 B． C． D．‎ ‎2．如图所示的几何体是由一些小立方块搭成的，则这个几何体的俯视图是（ ）‎ 第2题图 A．‎ B．‎ Ｃ．‎ D．‎ ‎3．在等边三角形、平行四边形、矩形、等腰梯形和圆中，既是轴对称图形又是中心对称图形的有（ ）‎ A．1种 B．2种 C．3种 D．4种 ‎4．在一个不透明的袋子里装有两个红球和两个黄球，它们除颜色外都相同．随机从中摸出一球，记下颜色后放回袋中，充分摇匀后，再随机摸出一球，两次都摸到黄球的概率是（ ）‎ A． B． C． D．‎ ‎5．如图所示，数轴上点所表示的可能是（ ）‎ O 第6题图 A． B． C． D．‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ P 第5题图 ‎6．一根水平放置的圆柱形输水管道横截面如图所示，其中有水部分水面宽‎0.8米，最深处水深‎0.2米，则此输水管道的直径是（ ）‎ A．‎0.4米 B．‎0.5米 C．‎0.8米 D．‎‎1米 ‎7．一块蓄电池的电压为定值，使用此蓄电池为电源时，电流（A）与电阻（Ω）之间的函数关系如图所示，如果以此蓄电池为电源的用电器限制电流不得超过‎10A，那么此用电器的可变电阻应（ ）‎ A．不小于4.8Ω B．不大于4.8Ω ‎ C．不小于14Ω D．不大于14Ω O x y 第8题图 A ‎6‎ O R/Ω I/A ‎8‎ 第7题图 ‎8．一艘轮船从港口出发，以15海里/时的速度沿北偏东60°的方向航行4小时后到达A处，此时观测到其正西方向50海里处有一座小岛B．若以港口为坐标原点，正东方向为轴的正方向，正北方向为轴的正方向，1海里为1个单位长度建立平面直角坐标系（如图），则小岛B所在位置的坐标是（ ）‎ A． B． C． D．‎ 二、填空题（本题满分18分，共有6道小题，每小题3分）‎ 请将9－14各小题的答案填写在第14小题后面给出表格的相应位置上 ‎9．我国首个火星探测器“萤火一号”已通过研制阶段的考核和验证，并将于今年下半年发射升空，预计历经约10个月，行程约380 000 000公里抵达火星轨道并定位．将380 000 000公里用科学记数法可表示为 公里．‎ ‎10．在第29届奥林匹克运动会上，青岛姑娘张娟娟为中国代表团夺得了历史上首枚奥运会射箭金牌，为祖国争得了荣誉．下表记录了她在备战奥运会期间的一次训练成绩（单位：环）：‎ 序号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 成绩 ‎9‎ ‎9‎ ‎10‎ ‎9‎ ‎8‎ ‎10‎ ‎10‎ ‎9‎ ‎8‎ ‎7‎ ‎10‎ ‎9‎ 根据表中的数据可得：张娟娟这次训练成绩的中位数是 环，众数是 环．‎ ‎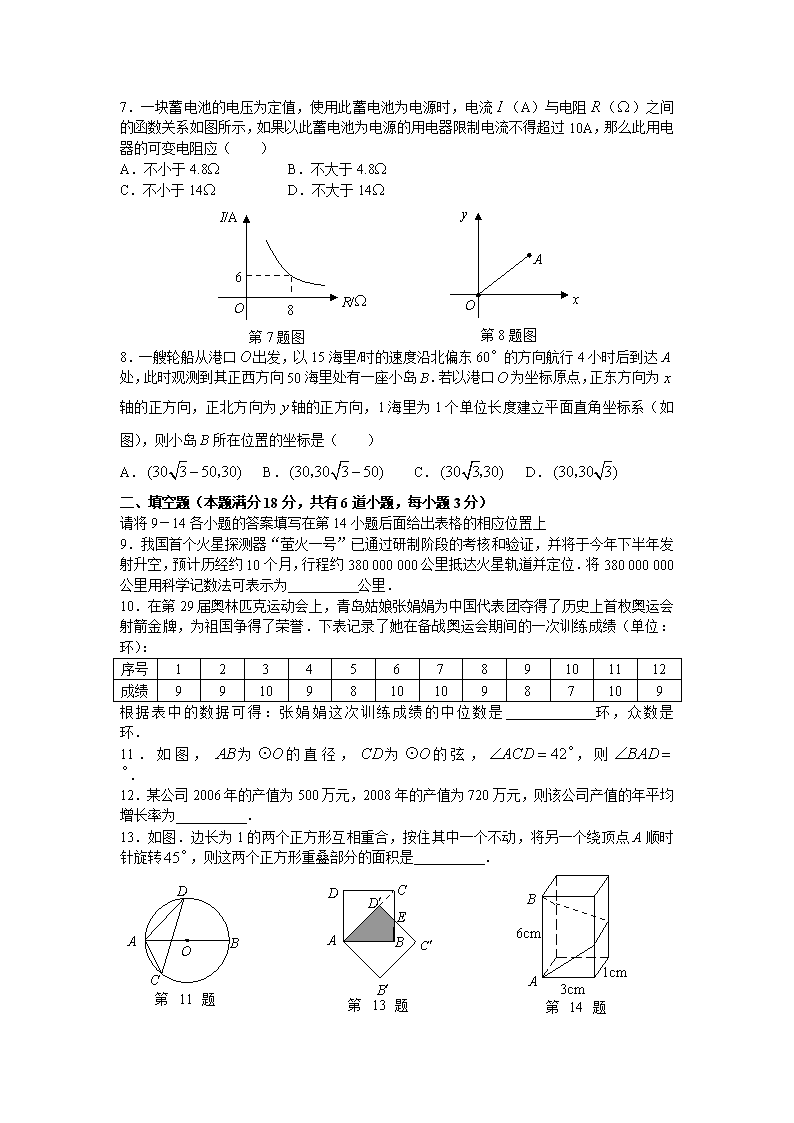11．如图，为的直径，为的弦，，则 ．‎ ‎12．某公司2006年的产值为500万元，2008年的产值为720万元，则该公司产值的年平均增长率为 ．‎ ‎13．如图．边长为1的两个正方形互相重合，按住其中一个不动，将另一个绕顶点A顺时针旋转，则这两个正方形重叠部分的面积是 ．‎ B A ‎6cm ‎3cm ‎1cm 第14题图 A D C B 第13题图 E O D A C B 第11题图 ‎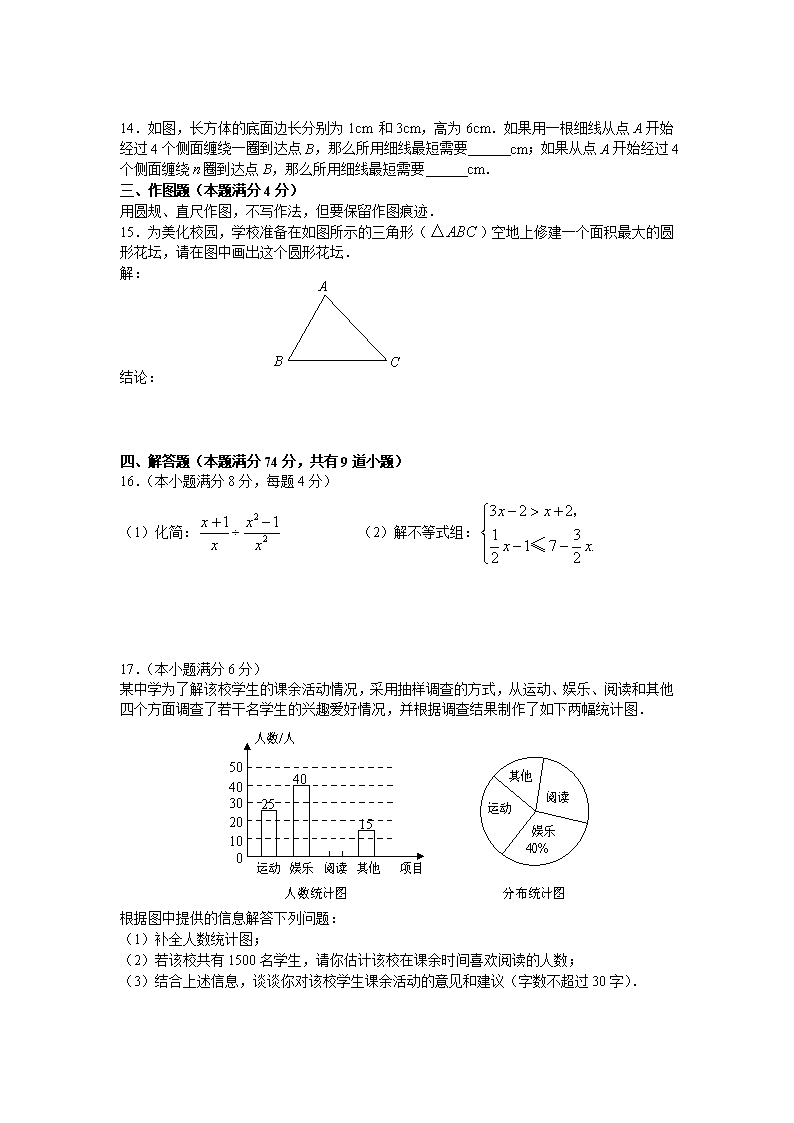14．如图，长方体的底面边长分别为‎1cm 和‎3cm，高为‎6cm．如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B，那么所用细线最短需要 cm；如果从点A开始经过4个侧面缠绕圈到达点B，那么所用细线最短需要 cm．‎ 三、作图题（本题满分4分）‎ 用圆规、直尺作图，不写作法，但要保留作图痕迹．‎ ‎15．为美化校园，学校准备在如图所示的三角形（）空地上修建一个面积最大的圆形花坛，请在图中画出这个圆形花坛．‎ A B C 解：‎ 结论：‎ 四、解答题（本题满分74分，共有9道小题）‎ ‎16．（本小题满分8分，每题4分）‎ ‎（1）化简： （2）解不等式组：‎ ‎17．（本小题满分6分）‎ 某中学为了解该校学生的课余活动情况，采用抽样调查的方式，从运动、娱乐、阅读和其他四个方面调查了若干名学生的兴趣爱好情况，并根据调查结果制作了如下两幅统计图．‎ ‎50‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ ‎0‎ 运动 娱乐 阅读 其他 项目 ‎40‎ ‎25‎ ‎15‎ 人数统计图 人数/人 阅读 其他 娱乐 运动 ‎40%‎ 分布统计图 根据图中提供的信息解答下列问题：‎ ‎（1）补全人数统计图；‎ ‎（2）若该校共有1500名学生，请你估计该校在课余时间喜欢阅读的人数；‎ ‎（3）结合上述信息，谈谈你对该校学生课余活动的意见和建议（字数不超过30字）．‎ ‎18．（本小题满分6分）‎ 在“六·一”儿童节来临之际，某妇女儿童用品商场为吸引顾客，设立了一个可以自由转动的转盘（如图，转盘被平均分成20份），并规定：顾客每购物满100元，就能获得一次转动转盘的机会．如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么顾客就可以分别获得80元、50元、20元的购物券，凭购物券可以在该商场继续购物．如果顾客不愿意转转盘，那么可直接获得15元的购物券．‎ 转转盘和直接获得购物券，你认为哪种方式对顾客更合算？请说明理由．‎ 红 黄 黄 绿 绿 绿 绿 黄 绿 第18题图 ‎19．（本小题满分6分）‎ 在一次数学活动课上，老师带领同学们去测量一座古塔CD的高度．他们首先从A处安置测倾器，测得塔顶C的仰角，然后往塔的方向前进‎50米到达B处，此时测得仰角，已知测倾器高‎1.5米，请你根据以上数据计算出古塔CD的高度．‎ C G E D B A F 第19题图 ‎（参考数据：，，，）‎ ‎20．（本小题满分8分）‎ 北京奥运会开幕前，某体育用品商场预测某品牌运动服能够畅销，就用32000元购进了一批这种运动服，上市后很快脱销，商场又用68000元购进第二批这种运动服，所购数量是第一批购进数量的2倍，但每套进价多了10元．‎ ‎（1）该商场两次共购进这种运动服多少套？‎ ‎（2）如果这两批运动服每套的售价相同，且全部售完后总利润率不低于20%，那么每套售价至少是多少元？（利润率）‎ ‎21．（本小题满分8分）‎ 已知：如图，在中，AE是BC边上的高，将沿方向平移，使点E与点C重合，得．‎ ‎（1）求证：；‎ A D G C B F E 第21题图 ‎（2）若，当AB与BC满足什么数量关系时，四边形是菱形？证明你的结论．‎ ‎22．（本小题满分10分）‎ 某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价（元）与销售月份（月）满足关系式，而其每千克成本（元）与销售月份（月）满足的函数关系如图所示．‎ ‎（1）试确定的值；‎ ‎（2）求出这种水产品每千克的利润（元）与销售月份（月）之间的函数关系式；‎ ‎（3）“五·一”之前，几月份出售这种水产品每千克的利润最大？最大利润是多少？‎ ‎25‎ ‎24‎ y2（元）‎ x（月）‎ ‎1 2 3 4 5 6 7 8 9 10 11 12 ‎ 第22题图 O ‎23．（本小题满分10分）‎ 我们在解决数学问题时，经常采用“转化”（或“化归”）的思想方法，把待解决的问题，通过某种转化过程，归结到一类已解决或比较容易解决的问题．‎ 譬如，在学习了一元一次方程的解法以后，进一步研究二元一次方程组的解法时，我们通常采用“消元”的方法，把二元一次方程组转化为一元一次方程；再譬如，在学习了三角形内角和定理以后，进一步研究多边形的内角和问题时，我们通常借助添加辅助线，把多边形转化为三角形，从而解决问题．‎ 问题提出：如何把一个正方形分割成（）个小正方形？‎ 为解决上面问题，我们先来研究两种简单的“基本分割法”．‎ 基本分割法1：如图①，把一个正方形分割成4个小正方形，即在原来1个正方形的基础上增加了3个正方形．‎ 基本分割法2：如图②，把一个正方形分割成6个小正方形，即在原来1个正方形的基础上增加了5个正方形．‎ 图①‎ 图②‎ 图③‎ 图④‎ 图⑤‎ 图⑥‎ 问题解决：有了上述两种“基本分割法”后，我们就可以把一个正方形分割成（）个小正方形．‎ ‎（1）把一个正方形分割成9个小正方形．‎ 一种方法：如图③，把图①中的任意1个小正方形按“基本分割法‎2”‎进行分割，就可增加5个小正方形，从而分割成（个）小正方形．‎ 另一种方法：如图④，把图②中的任意1个小正方形按“基本分割法‎1”‎进行分割，就可增加3个小正方形，从而分割成（个）小正方形．‎ ‎（2）把一个正方形分割成10个小正方形．‎ 方法：如图⑤，把图①中的任意2个小正方形按“基本分割法‎1”‎进行分割，就可增加个小正方形，从而分割成（个）小正方形．‎ ‎（3）请你参照上述分割方法，把图⑥给出的正方形分割成11个小正方形（用钢笔或圆珠笔画出草图即可，不用说明分割方法）‎ ‎（4）把一个正方形分割成（）个小正方形．‎ 方法：通过“基本分割法‎1”‎、“基本分割法‎2”‎或其组合把一个正方形分割成9个、10个和11个小正方形，再在此基础上每使用1次“基本分割法‎1”‎，就可增加3个小正方形，从而把一个正方形分割成12个、13个、14个小正方形，依次类推，即可把一个正方形分割成（）个小正方形．‎ 从上面的分法可以看出，解决问题的关键就是找到两种基本分割法，然后通过这两种基本分割法或其组合把正方形分割成（）个小正方形．‎ 类比应用：仿照上面的方法，我们可以把一个正三角形分割成（）个小正三角形．‎ ‎（1）基本分割法1：把一个正三角形分割成4个小正三角形（请你在图a 中画出草图）．‎ ‎（2）基本分割法2：把一个正三角形分割成6个小正三角形（请你在图b 中画出草图）．‎ ‎（3）分别把图c、图d和图e中的正三角形分割成9个、10个和11个小正三角形（用钢笔或圆珠笔画出草图即可，不用说明分割方法）‎ 图a 图b 图c 图d 图e ‎（4）请你写出把一个正三角形分割成（）个小正三角形的分割方法（只写出分割方法，不用画图）．‎ ‎24．（本小题满分12分）‎ 如图，在梯形ABCD中，，，，，点由B出发沿BD方向匀速运动，速度为‎1cm/s；同时，线段EF由DC出发沿DA方向匀速运动，速度为‎1cm/s，交于Q，连接PE．若设运动时间为（s）（）．解答下列问题：‎ ‎（1）当为何值时，？‎ ‎（2）设的面积为（cm2），求与之间的函数关系式；‎ ‎（3）是否存在某一时刻，使？若存在，求出此时的值；若不存在，说明理由．‎ ‎（4）连接，在上述运动过程中，五边形的面积是否发生变化？说明理由．‎ A E D Q P B F C 第24题图 二○○九年山东省青岛市初级中学学业水平考试 数学试题参考答案及评分标准 说明：‎ ‎1．如果考生的解法与本解法不同，可参照本评分标准制定相应评分细则．‎ ‎2．当考生的解答在某一步出现错误，影响了后继部分时，如果这一步以后的解答未改变这道题的内容和难度，可视影响程度决定后面部分的给分．但不得超过后面部分应给分数的一半，如果这一步以后的解答有较严重的错误，就不给分．‎ ‎3．为阅卷方便，本解答中的推算步骤写得较为详细，但允许考生在解答过程中，合理省略非关键性的推算步骤．‎ ‎4．解答右端所注分数，表示考生正确做到这一步应得的累加分数．‎ 一、选择题（本题满分24分，共有8道小题，每小题3分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 C D B C B D A A 二、填空题（本题满分18分，共有6道小题，每小题3分）‎ 题号 ‎9‎ ‎10‎ ‎11‎ 答案 ‎9‎ ‎9‎ ‎48‎ 题号 ‎12‎ ‎13‎ ‎14‎ 答案 ‎20%‎ ‎（或）‎ 三、作图题（本题满分4分）‎ ‎15．正确画出两条角平分线，确定圆心； 2分 确定半径； 3分 正确画出图并写出结论． 4分 四、解答题（本题满分74分，共有9道小题）‎ ‎16．（本小题满分8分）‎ ‎（1）解：原式 ‎ ． 4分 ‎（2）‎ 解：解不等式①得 ，‎ 解不等式②得 ．‎ 所以原不等式组的解集为． 4分 ‎17．（本小题满分6分）‎ 解：（1）正确补全统计图； 2分 ‎（2）300人． 4分 ‎（3）合理即可． 6分 ‎18．（本小题满分6分）‎ 解：（元）， 4分 ‎∵‎ ‎∴选择转转盘对顾客更合算． 6分 ‎19．（本小题满分6分）‎ C G E D B A F 第19题图 解：由题意知，，‎ ‎∴，设，‎ 在中，‎ ‎，则；‎ 在中，‎ ‎，‎ 则； 4分 ‎∵，‎ ‎∴．‎ ‎ ，‎ ‎∴（米）．‎ 答：古塔的高度约是‎39米． 6分 ‎20．（本小题满分8分）‎ 解：（1）设商场第一次购进套运动服，由题意得：‎ ‎， 3分 解这个方程，得．‎ 经检验，是所列方程的根．‎ ‎．‎ 所以商场两次共购进这种运动服600套． 5分 ‎（2）设每套运动服的售价为元，由题意得：‎ ‎，‎ 解这个不等式，得，‎ 所以每套运动服的售价至少是200元． 8分 ‎21．（本小题满分8分）‎ 证明：（1）∵四边形是平行四边形，‎ ‎∴．‎ ‎∵是边上的高，且是由沿方向平移而成．‎ ‎∴．‎ ‎∴．‎ ‎∵，‎ ‎∴．‎ ‎∴． 4分 ‎（2）当时，四边形是菱形．‎ ‎∵，，‎ A D G C B F E 第21题图 ‎∴四边形是平行四边形．‎ ‎∵中，，‎ ‎∴，‎ ‎∴．‎ ‎∵，‎ ‎∴．‎ ‎∴．‎ ‎∴四边形是菱形． 8分 ‎22．（本小题满分10分）‎ 解：（1）由题意：‎ 解得 4分 ‎（2）‎ ‎ ‎ ‎ ； 6分 ‎（3）‎ ‎ ‎ ‎ ‎ ‎∵，‎ ‎∴抛物线开口向下．‎ 在对称轴左侧随的增大而增大．‎ 由题意，所以在4月份出售这种水产品每千克的利润最大． 9分 最大利润（元）． 10分 ‎23．（本小满分10分）‎ 解：把一个正方形分割成11个小正方形：‎ 图⑥‎ ‎ 2分 把一个正三角形分割成4个小正三角形：‎ 图a ‎ 3分 把一个正三角形分割成6个小正三角形：‎ 图b ‎ 5分 把一个正三角形分割成9个、10个和11个小正三角形：‎ 图c 图e 图d ‎ 8分 把一个正三角形分割成（）个小正三角形的分割方法：通过“基本分割法‎1”‎、“基本分割法‎2”‎或其组合，把一个正三角形分割成9个、10个和11个小正三角形，再在此基础上每使用1次“基本分割法‎1”‎，就可增加3个小正三角形，从而把一个正三角形分割成12个、13个、14个小正三角形，依次类推，即可把一个正三角形分割成（）个小正三角形． 10分 ‎24．（本小题满分12分）‎ 解：（1）∵‎ A E D Q P B F C N M ‎∴．‎ 而，‎ ‎∴，‎ ‎∴．‎ ‎∴当． 2分 ‎（2）∵平行且等于，‎ ‎∴四边形是平行四边形．‎ ‎∴．‎ ‎∵，‎ ‎∴．‎ ‎∴．‎ ‎∴．‎ ‎．‎ ‎∴．‎ 过B作，交于，过作，交于．‎ ‎．‎ ‎∵，‎ ‎∴．‎ 又，‎ ‎，‎ ‎，‎ ‎． 6分 ‎（3）．‎ 若，‎ 则有，‎ 解得． 9分 ‎（4）在和中，‎ ‎∴‎ ‎ ‎ ‎ ．‎ ‎∴在运动过程中，五边形的面积不变． 12分