2013淄博中考数学试题含答案 8页

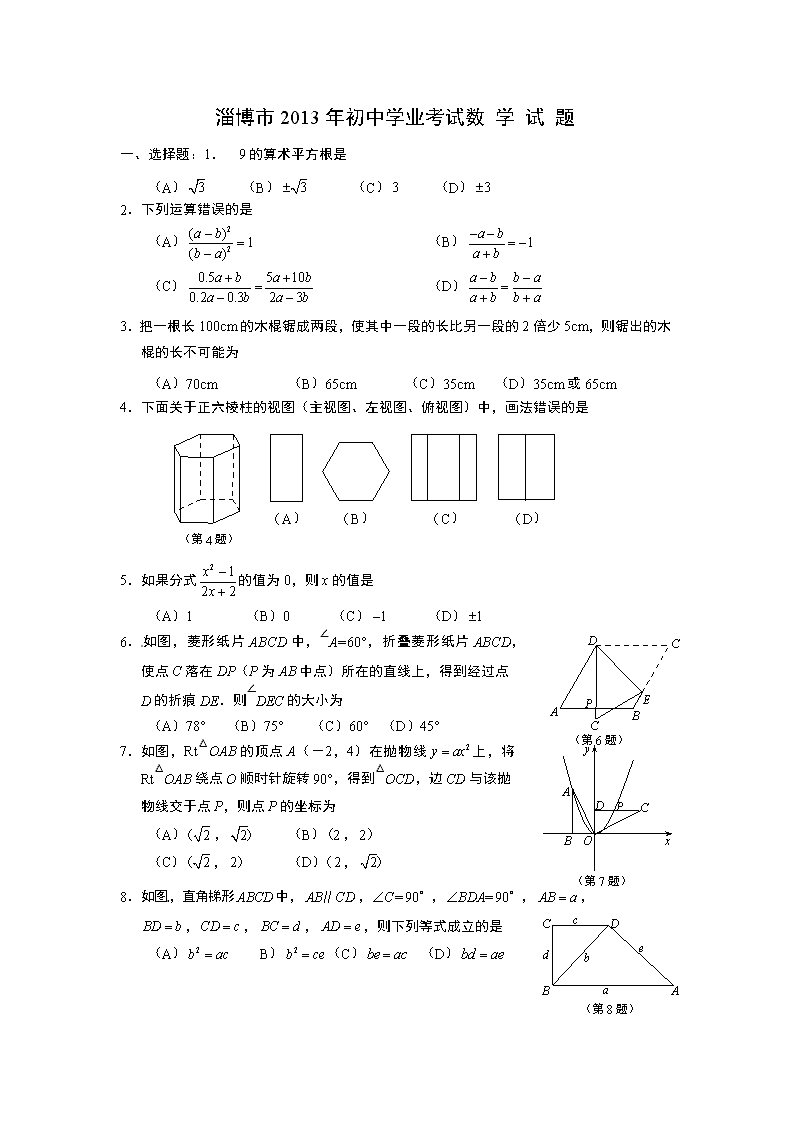
淄博市2013年初中学业考试数 学 试 题 一、选择题：1． 9的算术平方根是 ‎ （A） （B） （C） （D）‎ ‎2．下列运算错误的是 ‎ （A） （B）‎ ‎ （C） （D）‎ ‎3．把一根长‎100cm的木棍锯成两段，使其中一段的长比另一段的2倍少‎5cm，则锯出的木棍的长不可能为 ‎ （A）‎70cm （B）65cm （C）35cm （D）‎35cm或‎65cm ‎4．下面关于正六棱柱的视图（主视图、左视图、俯视图）中，画法错误的是 ‎（第4题）‎ ‎（D）‎ ‎（C）‎ ‎（B）‎ ‎（A）‎ ‎5．如果分式的值为0，则x的值是 ‎ （A）1 （B）0 （C） （D）‎ ‎（第6题）‎ A B C D E C P ‎6．如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，‎ 使点C落在DP（P为AB中点）所在的直线上，得到经过点 D的折痕DE．则∠DEC的大小为 ‎ （A）78° （B）75° （C）60° （D）45°‎ ‎7．如图，Rt△OAB的顶点A（－2，4）在抛物线上，将 ‎（第7题）‎ A O B C D P x y Rt△OAB绕点O顺时针旋转90°，得到△OCD，边CD与该抛 物线交于点P，则点P的坐标为 ‎ （A）， （B），‎ ‎ （C）， （D），‎ ‎8．如图，直角梯形ABCD中，，90°，90°，，‎ A B C D d a b c e ‎（第8题）‎ ‎，，，，则下列等式成立的是 ‎ （A） B）（C） （D）‎ ‎9．如图，矩形AOBC的面积为4，反比例函数的图象的一支经过 y A O B C P x ‎（第9题）‎ 矩形对角线的交点P，则该反比例函数的解析式是 ‎ （A） （B）‎ ‎ （C） （D）‎ ‎10．如果m是任意实数，则点，一定不在 ‎ （A）第一象限 （B）第二象限 ‎ （C）第三象限 （D）第四象限 ‎11．假定鸟卵孵化后，雏鸟为雌与雄的概率相同．如果三枚卵全部成功孵化，则三只雏鸟中恰有两只雌鸟的概率是 ‎ （A） （B） （C） （D）‎ A B C D E P Q ‎（第12题）‎ ‎12．如图，△ABC的周长为26，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC=10，则PQ的长为 ‎ （A） （B） （C）3 （D）4‎ 二、填空题：．‎ ‎13．当实数a＜0时，6+a　　　6-a（填“＜”或“＞”）.‎ ‎14．请写出一个概率小于的随机事件：　　　　　　　　　　　　　　　　　　　　　　.‎ ‎15．在△ABC中，P是AB上的动点（P异于A，B），过点P的一条直线截△ABC，使截得的三角形与△ABC相似，我们不妨称这种直线为过点P的△ABC的相似线．如图，∠A=36°，AB=AC，当点P在AC的垂直平分线上时，过点P的△ABC的相似线最多有　　　条.‎ A B C P ‎（第15题）‎ D A B E C O ‎（第16题）‎ ‎16．如图，AB是⊙O的直径，，AB=5，BD=4，则sin∠ECB=　　　.‎ ‎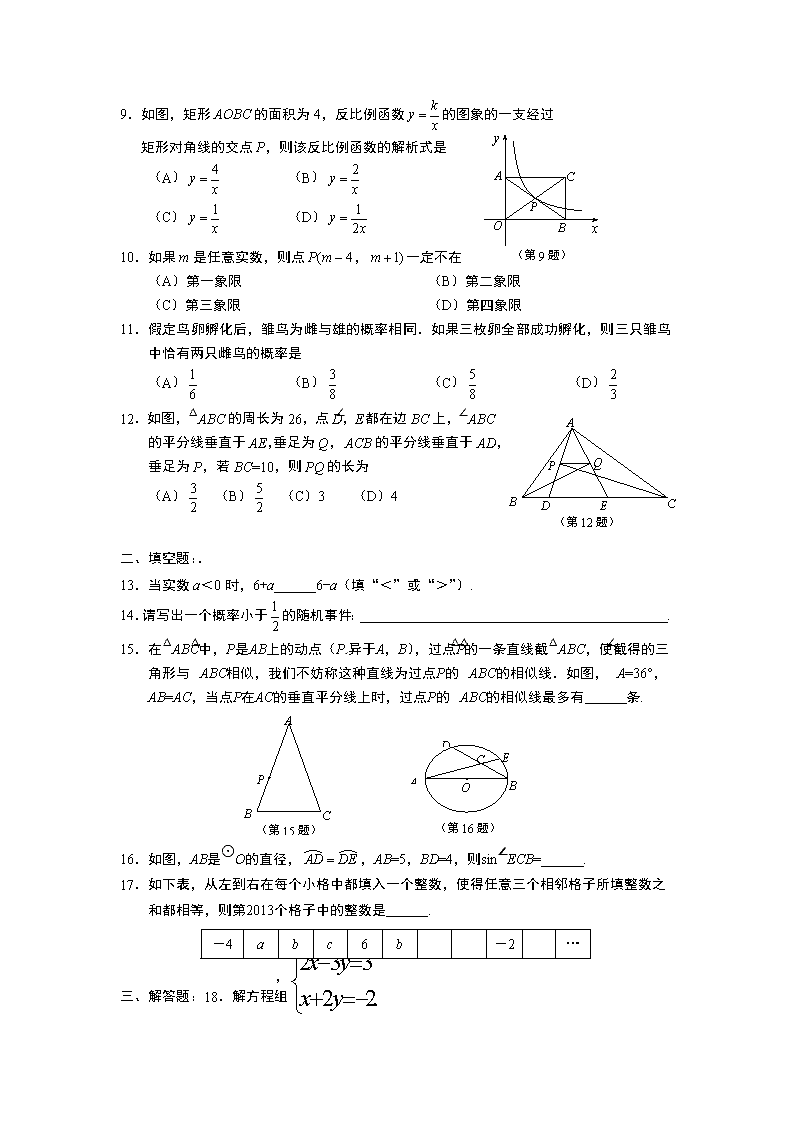17．如下表，从左到右在每个小格中都填入一个整数，使得任意三个相邻格子所填整数之和都相等，则第2013个格子中的整数是　　　.‎ ‎－4‎ a b c ‎6‎ b ‎－2‎ ‎…‎ 三、解答题：18．‎，‎ 解方程组 ‎（第19题）‎ C D A B ‎19．如图，AD∥BC，BD平分∠ABC．求证：AB=AD.‎ ‎20．某中学积极开展跳绳活动，体育委员统计了全班同学1分钟跳绳的次数，并列出了频数分布表：‎ 次数 ‎60≤x＜80‎ ‎80≤x＜100‎ ‎100≤x＜120‎ ‎120≤x＜140‎ ‎140≤x＜160‎ ‎160≤x＜180‎ 频数 ‎5‎ ‎6‎ ‎14‎ ‎9‎ ‎4‎ ‎（1）跳绳次数x在120≤x＜140范围的同学占全班同学的20%，在答题卡中完成上表；‎ ‎（2）画出适当的统计图，表示上面的信息.‎ ‎21．关于x的一元二次方程有实根.‎ ‎（1）求a的最大整数值；‎ ‎（2）当a取最大整数值时，①求出该方程的根；②求的值.‎ ‎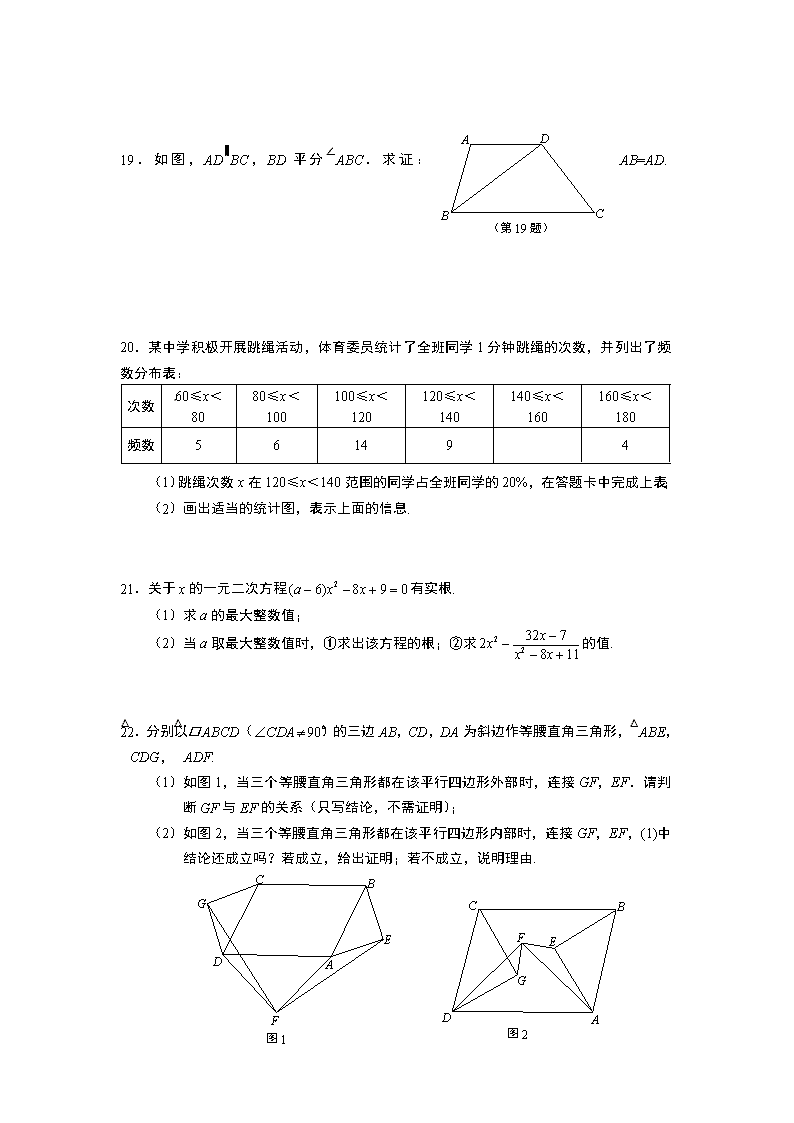22．分别以□ ABCD（90°）　的三边AB，CD，DA为斜边作等腰直角三角形，△ABE，△CDG，△ADF.‎ ‎（1）如图1，当三个等腰直角三角形都在该平行四边形外部时，连接GF，EF．请判断GF与EF的关系（只写结论，不需证明）；‎ ‎（2）如图2，当三个等腰直角三角形都在该平行四边形内部时，连接GF，EF，(1)中结论还成立吗？若成立，给出证明；若不成立，说明理由.‎ A B C D G F E 图1‎ A B C D G F E 图2‎ ‎ ‎ ‎23．△ABC是等边三角形，点A与点D的坐标分别是A（4，0），D（10，0）.‎ ‎（1）如图1，当点C与点O重合时，求直线BD的解析式；‎ ‎（2）如图2，点C从点O沿y轴向下移动，当以点B为圆心，AB为半径的⊙B与y轴相切（切点为C）时，求点B的坐标；‎ ‎（3）如图3，点C从点O沿y轴向下移动，当点C的坐标为C（0，）时，求∠ODB的正切值.‎ ‎24．矩形纸片ABCD中，AB=5，AD=4.‎ ‎（1）如图1，四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形．你能否在该矩形中裁剪出一个面积最大的正方形，最大面积是多少？说明理由；‎ ‎（2）请用矩形纸片ABCD剪拼成一个面积最大的正方形．要求：在图2的矩形ABCD中画出裁剪线，并在网格中画出用裁剪出的纸片拼成的正方形示意图（使正方形的顶点都在网格的格点上）.‎ A B C D M N E F 图1‎ 图2‎ D C B A 淄博市2013年初中学业考试 数学试题（A卷）参考答案及评分标准 评卷说明：‎ ‎1．选择题和填空题中的每小题，只有满分和零分两个评分档，不给中间分．‎ ‎2．解答题每小题的解答中所对应的分数，是指考生正确解答到该步骤所应得的累计分数．每小题只给出一种或两种解法，对考生的其它解法，请参照评分意见进行评分．‎ ‎3．如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续部分酌情给分，但最多不超过正确解答分数的一半；若出现严重的逻辑错误，后续部分就不再给分．‎ 一、选择题（本大题共12小题，每小题每题4分，共48分．错选、不选或选出的答案超过一个，均记零分）： ‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 C D A A A[‎ B C A C D B C 二、填空题 (本大题共5小题，每小题4分，共20分) ：‎ ‎13．； 14．答案不唯一. 如：掷一个骰子，向上一面的点数为2；‎ ‎15．3； 16．； 17．－2． ‎ 三、解答题 (本大题共7小题，共52分) ：‎ ‎18．(本题满分5分)‎ ‎②‎ ‎①‎ 解：‎ ‎①－2×②，得 －7y=7，‎ y=－1. …………………………………3′‎ 把y=－1带入②，得 x=0. …………………………………4′‎ 所以这个方程组的解为…………………………………5′‎ ‎19．(本题满分5分) ‎ 证明：∵AD∥BC，‎ ‎∴∠ADB=∠CBD.…………………………………………2′‎ ‎∵BD平分∠ABC，‎ ‎∴∠CBD=∠ABD.…………………………………………3′‎ ‎∴∠ADB =∠ABD.‎ ‎∴AB=AD.……………………………………………………5′‎ 次数/个 频数 学生人数 ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎12‎ ‎14‎ ‎60‎ ‎80‎ ‎100‎ ‎120‎ ‎140‎ ‎160‎ ‎180‎ ‎0‎ ‎20．(本题满分8分) ‎ ‎ 解(1)7………3′‎ ‎(2)如图………8′‎ ‎21．（本题满分8分）‎ 解：(1)△==－‎36a+280，……………………1′‎ ‎∵该方程有实根，‎ ‎∴△≥0，即－‎36a+280≥0 ， a≤.……………………2′‎ ‎∴a的最大整数值为7.…………………………………………3′‎ ‎(2) ①一元二次方程为，‎ ‎.‎ ‎.…………………………………………5′‎ ‎ ②∵，‎ ‎∴.…………………………………………6′‎ ‎…………………………7′‎ ‎=.…………………8′‎ ‎22．（本题满分8分）‎ 解：(1)GF⊥EF，GF=EF.………………………………………………………2′‎ ‎(2)GF⊥EF，GF=EF成立.………………………………………………………3′‎ 证明：∵四边形ABCD是平行四边形，‎ ‎∴AB=DC，∠DAB+∠ADC=180°.‎ ‎∵△ABE，△CDG，△ADF. 都是等腰直角三角形，‎ ‎∴DG=AE，DF=AF，∠CDG=∠ADF=∠DAF=∠BAE=45°.…………………5′‎ ‎∴∠BAE+∠DAF+∠EAF+∠ADF+∠CDF =180°.‎ ‎∴∠EAF+∠CDF =45°.‎ ‎∵∠CDF+∠GDF =45°，‎ ‎∴∠GDF=∠EAF.‎ ‎∴△GDF≌△EAF.………………………………………………………………6′‎ ‎∴GF=EF，∠GFD=∠EFA.即∠GFD+∠GFA =∠EFA+∠GFA ‎∴∠GFE=∠DFA=90°. ‎ ‎∴GF⊥EF.…………………………………………………………………………8′‎ ‎23．（本题满分9分）‎ ‎ 解：(1)∵A（4,0），‎ ‎ ∴OA=4，等边三角形△ABC的高为 ‎∴B点的坐标为（2,－2）.…………………………………………1′‎ ‎ 设直线BD的解析式为：‎ ‎ 则 解得 ‎∴直线BD的解析式为：.………………………………3′‎ ‎ (2)∵以AB为半径的⊙B与y轴相切于点C，‎ ‎∴BC与y轴垂直.‎ ‎∵△ABC是等边三角形，A（4,0），‎ ‎∴B点的坐标为（8，－4）.…………………………………………5′‎ ‎(3)以点B为圆心，AB为半径作⊙B，交y轴于C，E，过点B作BF⊥CE垂足为F，‎ 连接AE.…………………………………………6′‎ x y O A B C D 图3‎ E F P Q ‎∵△ABC是等边三角形，A（4,0），‎ ‎∴∠OEA=∠ABC=30°.‎ ‎∴AE=8.‎ 在Rt △OAE中，‎ ‎∴OE=.‎ ‎∵OC=，‎ ‎∴AC=.………………………………7′‎ ‎∴CE=OE－OC=.‎ ‎∴OF=OC+CF=.‎ 在Rt △CFB中，‎ ‎=25， BF=5‎ ‎∴B点的坐标为(5,) ， ‎ 过点B作x轴的垂线，垂足为Q，‎ tan∠ODB=.…………………………………………9′‎ ‎24．（本题满分9分）‎ 解：（1）正方形的最大面积是16.…………………………………………1′‎ 设AM=x(0≤x≤4) ，‎ 则MD=4－x.‎ ‎∵四边形MNEF是正方形，‎ ‎∴MN=MF，∠AMN+∠FMD=90°.‎ ‎∵∠AMN+∠ANM=90°，‎ ‎∴∠ANM=∠FMD.‎ ‎∴Rt△ANM≌Rt△DMF.…………………………………………2′‎ ‎∴DM=AN.‎ ‎∴‎ x y O ‎2‎ ‎16‎ ‎.………………………4′‎ ‎∵函数的开口向上，‎ 对称轴是x=2，‎ 函数图象如图所示，‎ ‎∵0≤x≤4，‎ ‎∴当x=0或x=4时，‎ 正方形MNEF的面积最大.‎ 最大值是16.……………………5′‎ ‎(2)如图，画出分割线7′；‎ 拼出图形9′.‎ A B C D