- 386.00 KB
- 2021-05-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第25课时 相似三角形
课 题
第25课时 相似三角形
教学时间
教学目标:
1、理解相似三角形性质。
2、掌握两个三角形相似的条件,知道两角对应相等的两三角形相似,两边对应成比例且夹角相等的三角形相似,三边对应成比例的两个三角形相似。
3、能应用图形相似解决一些实际问题,会把实际问题转化为数学问题。
教学重点:
把实际问题转化成相似三角形的数学模型
教学难点:
把实际问题转化成相似三角形的数学模型
教学方法:
自主探究 合作交流 讲练结合
教学媒体:
电子白板
【教学过程】:
一知识梳理
1、相似三角形的定义
________________________________ 三角形叫做相似三角形.
2、相似三角形的判定
(1)_________________________,两三角形相似.
(2)_________________________,两三角形相似.
(3)_________________________,两三角形相似.
3、相似三角形的性质
(1)相似三角形的对应角________,对应边________.
(2)相似三角形的周长比等于________.
(3)相似三角形的对应边上的高、中线、角平分线的比等于_______.
(4)相似三角形的面积比等于________________.
二典型例题
1.相似三角形的判定
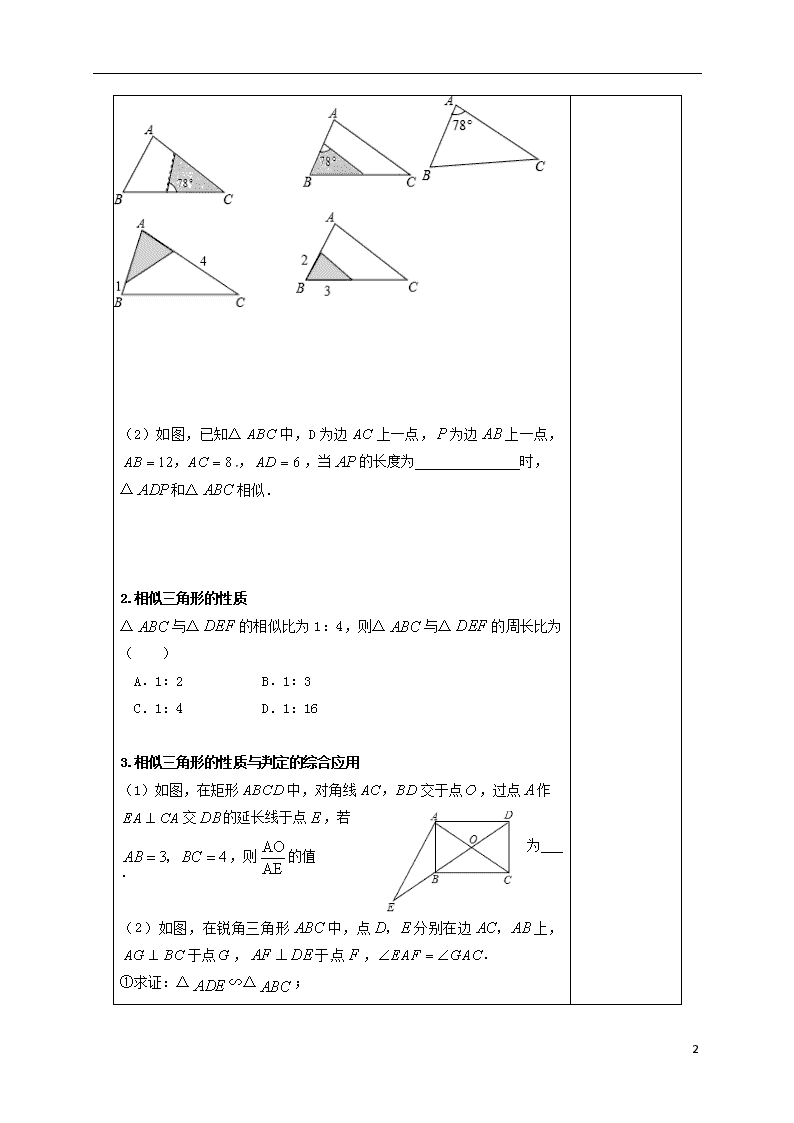
(1)(中考指要P93第3题)如图,△中,,.将△沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
复 备 栏
5
(2)如图,已知△中,D为边上一点,为边上一点,,,当的长度为 时,
△和△相似.
2.相似三角形的性质
△与△的相似比为1:4,则△与△的周长比为( )
A.1:2 B.1:3
C.1:4 D.1:16
3.相似三角形的性质与判定的综合应用
(1)如图,在矩形中,对角线交于点,过点作交的延长线于点,若,则的值为 .
(2)如图,在锐角三角形中,点分别在边上,于点,于点,
①求证:△∽△;
5
②若,求的值.
(3)(中考指要例1)如图,在等腰三角形中,,点是边上的一个动点,在上取一点,使.
①求证:△∽△;
②设,求关于的函数关系式并写出自变量的取值范围;
③求的最小值。
④若点在线段上运动,则点的运动路径长为 。
(4)(中考指要例2)(2015武汉)已知锐角△中,边长为12,高长为8
(1) 如图,矩形的边在边上,其余两个顶点分别在边上,交于点
5
① 求的值。
② 设,矩形的面积为,求与的函数关系式,并求的最大值
(2) 若,正方形的两个顶点在△一边上,另两个顶点分别在△的另两边上,直接写出正方形的边长
三、中考预测
如图,已知为的边上的一点,且.以为顶点的 的两边分别交射线于两点,且.当以点为旋转中心,边与重合的位置开始,按逆时针方向旋转(保持不变)时,两点在射线上同时以不同的速度向右平行移动.设(),△的面积为S .
(1)判断:△与△是否相似,并说明理由;
(2)写出与之间的关系式;
(3)试写出随变化的函数关系式,并确定的取值范围.
M
N
B
P
A
O
5
四、反思总结
1.本节课你复习了哪些内容?
2.通过本节课的学习,你还有哪些困难?
5