2018成都中考数学模拟试卷3 4页

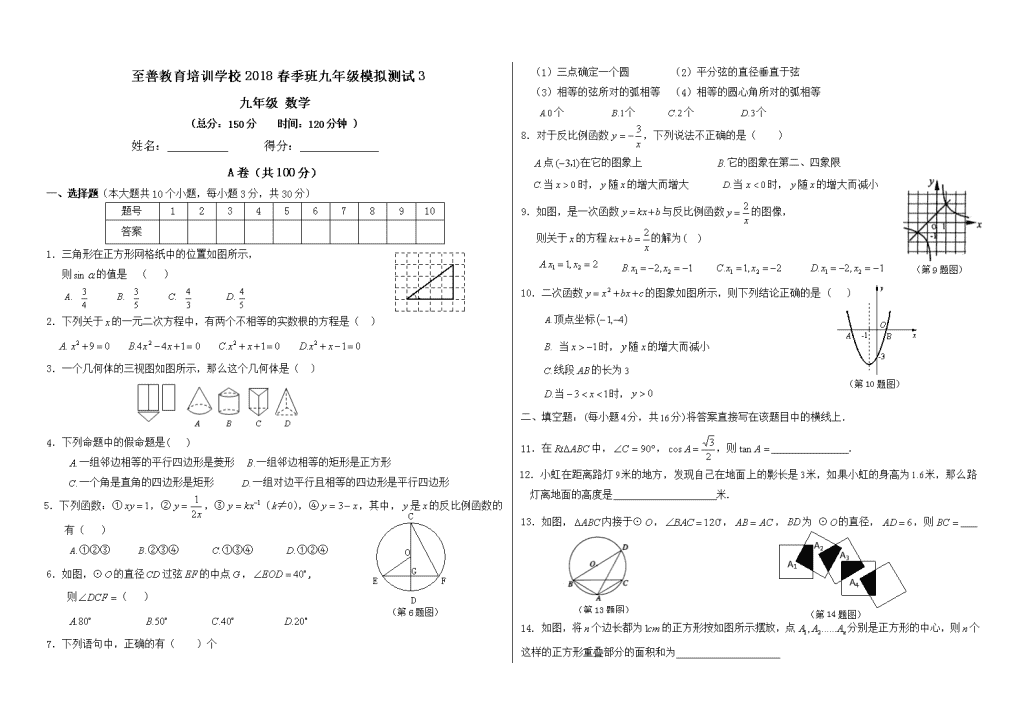
‎ 至善教育培训学校2018春季班九年级模拟测试3‎ 九年级 数学 ‎（总分：150分 时间：120分钟 ）‎ 姓名： 得分： ；‎ A卷（共100分）‎ 一、选择题（本大题共10个小题，每小题3分，共30分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 ‎1．三角形在正方形网格纸中的位置如图所示，‎ 则的值是 （ ）‎ ‎ ‎ ‎2．下列关于的一元二次方程中，有两个不相等的实数根的方程是（　）‎ ‎ 　 ‎ ‎3．一个几何体的三视图如图所示，那么这个几何体是（ ） ‎ ‎4．下列命题中的假命题是( )‎ ‎ 一组邻边相等的平行四边形是菱形 一组邻边相等的矩形是正方形 ‎ 一个角是直角的四边形是矩形 一组对边平行且相等的四边形是平行四边形 ‎（（第6题图）‎ ‎5．下列函数：①，②，③（k≠0），④，其中，是的反比例函数的有（ ）‎ ‎①②③ ②③④ ①③④ ①②④‎ ‎6．如图，⊙的直径过弦的中点，,‎ 则（ ）‎ ‎ ‎ ‎7．下列语句中，正确的有（ ）个 ‎（1）三点确定一个圆 （2）平分弦的直径垂直于弦 ‎（3）相等的弦所对的弧相等 （4）相等的圆心角所对的弧相等 个 个 个 个 8． 对于反比例函数，下列说法不正确的是（ ）‎ ‎（（第9题图）‎ ‎ 点在它的图象上 它的图象在第二、四象限 当时，随的增大而增大 当时，随的增大而减小 ‎9．如图，是一次函数与反比例函数的图像，‎ 则关于的方程的解为( )‎ ‎ ‎ ‎（第10题图）‎ ‎10．二次函数的图象如图所示，则下列结论正确的是 ( )‎ 顶点坐标 ‎ ‎ 当时，随的增大而减小 线段的长为 ‎ 当时， ‎ 二、填空题：(每小题分，共分)将答案直接写在该题目中的横线上．‎ ‎11．在中，，，则 ． ‎ ‎12．小虹在距离路灯米的地方，发现自己在地面上的影长是米，如果小虹的身高为米，那么路灯离地面的高度是 米.　 ‎ ‎（（第13题图）‎ ‎、（DI）‎ A1‎ A2‎ A3‎ A4‎ ‎（第14题图）‎ ‎13．如图，内接于⊙，，，为 ⊙的直径，，则 ‎ ‎14. 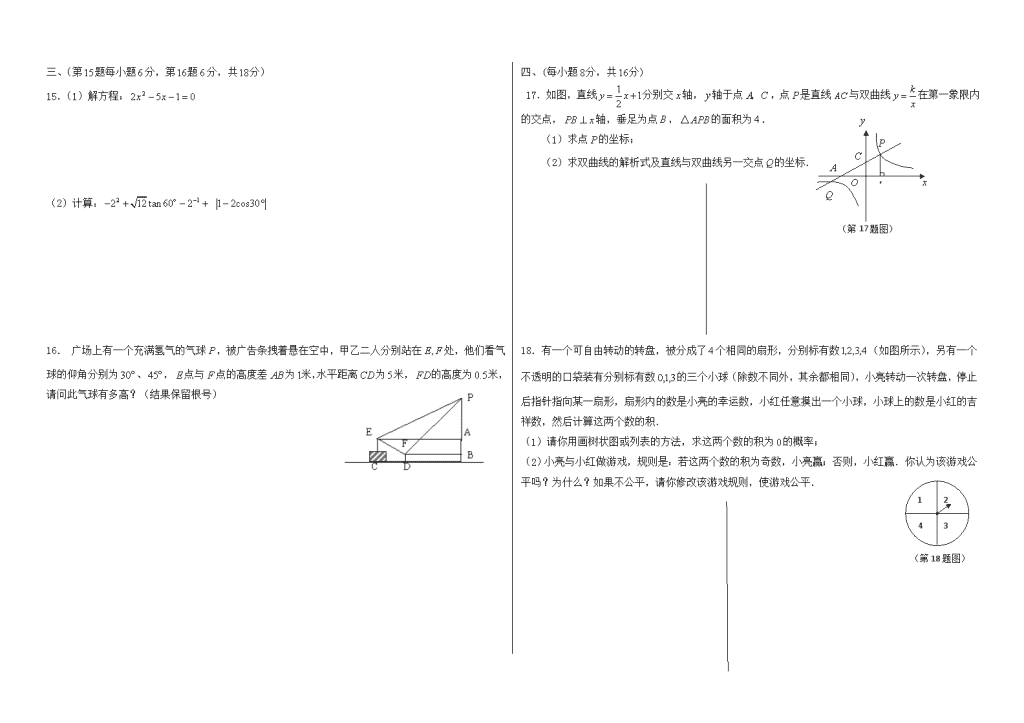如图，将个边长都为的正方形按如图所示摆放，点分别是正方形的中心，则个这样的正方形重叠部分的面积和为 ‎ 三、（第题每小题分，第题分，共分）‎ ‎15．（1）解方程： ‎ ‎（2）计算： ‎ ‎16． 广场上有一个充满氢气的气球，被广告条拽着悬在空中，甲乙二人分别站在处，他们看气球的仰角分别为、，点与点的高度差为米，水平距离为米，的高度为米，请问此气球有多高？（结果保留根号）‎ 四、(每小题分，共分)‎ ‎（第17题图）‎ ‎ 17．如图，直线分别交轴，轴于点，点是直线与双曲线在第一象限内的交点，轴，垂足为点，的面积为．‎ ‎（1）求点的坐标；‎ ‎（2）求双曲线的解析式及直线与双曲线另一交点的坐标．‎ ‎18．有一个可自由转动的转盘，被分成了个相同的扇形，分别标有数（如图所示），另有一个不透明的口袋装有分别标有数的三个小球（除数不同外，其余都相同），小亮转动一次转盘，停止后指针指向某一扇形，扇形内的数是小亮的幸运数，小红任意摸出一个小球，小球上的数是小红的吉祥数，然后计算这两个数的积．‎ ‎（1）请你用画树状图或列表的方法，求这两个数的积为的概率；‎ ‎（第18题图）‎ ‎1‎ ‎2‎ ‎4‎ ‎3‎ ‎（（第18题图）‎ ‎（2）小亮与小红做游戏，规则是：若这两个数的积为奇数，小亮赢；否则，小红赢．你认为该游戏公平吗？为什么？如果不公平，请你修改该游戏规则，使游戏公平．‎ ‎ ‎ 五、(每小题分，共分)‎ ‎19．已知：如图，在□中，分别为边的中点，是对角线，交的延长线于．‎ ‎（（第19题图）‎ ‎（1）求证：△；‎ ‎（2）若四边形 是菱形，则四边形是什么特殊四边形？‎ 并证明你的结论．‎ ‎ 20．如图，⊙是的外接圆，为直径，于于，‎ ‎(1)判断的形状；‎ 第20题图 A B D E O F C ‎(2)设⊙的半径为，且，求证≌． ‎ B 卷(共50分)‎ F ‎（（第22题图）‎ ‎ 一、填空题：(每小题分，共分)将答案直接写在该题目中的横线上．‎ ‎21．已知，那么的值是 ．‎ ‎22．如图，是⊙上的三点，以为一边，作 过上一点，作交于点．若则点于,‎ y ‎1‎ x O · A B C A ‎，则 ． ‎ ‎23. 如图：等腰直角三角形ABC位于第一象限，，直角顶点 在直线上，其中点的横坐标为，且两条直角边分别平行于 轴、轴，若双曲线()与有交点，则的取值 范围是 ．‎ ‎24．二次函数的图象如图所示，有下列个结论：‎ ‎① ；② ；③ ；④ ；‎ ‎⑤ ，（的实数）‎ 其中正确的结论是 ．‎ ‎ （第24题图）‎ 25． 完全相同的个小球，上面分别标有数字，将其放入一个不透明的盒子中摇匀，再从中随机摸球两次(第一次摸出球后放回摇匀)．把第一次、第二次摸到的球上标有的数字分别记作以分别作为一个点的横坐标与纵坐标，定义点在反比例函数上为事件（为整数），当 的概率最大时，则的所有可能的值为 ．‎ 二、(共30分)‎ ‎26．（8分）已知关于的一元二次方程的两根是一个矩形两邻边的长．‎ ‎(1)取何值时，方程有两个正实数根(分)；(2)当矩形的对角线长为时，求的值(分)．‎ ‎ ‎ ‎27．（10分）如图，中，点都是斜边上的动点，点从向运动（不与点重合），点从向运动，．点分别是点以为对称中心的对称点，于，交点当点到达顶点时，同时停止运动．设的长为的面积为．（1）求证：∽（2）求关于的函数解析式并求的最大值；（3）当为何值时，为等腰三角形？‎ ‎ ‎ ‎28．（12分）如图，二次函数的图象经过点，且顶点的横坐标为，该图象在轴上截得的线段的长为.‎ ‎⑴求二次函数的解析式；‎ ‎⑵在该抛物线的对称轴上找一点，使最小，求出点的坐标；‎ ‎⑶在抛物线上是否存在点，使与相似？如果存在，求出点的坐标；如果不存在，请说明理由．‎