中考专题几何综合之旋转专题 46页

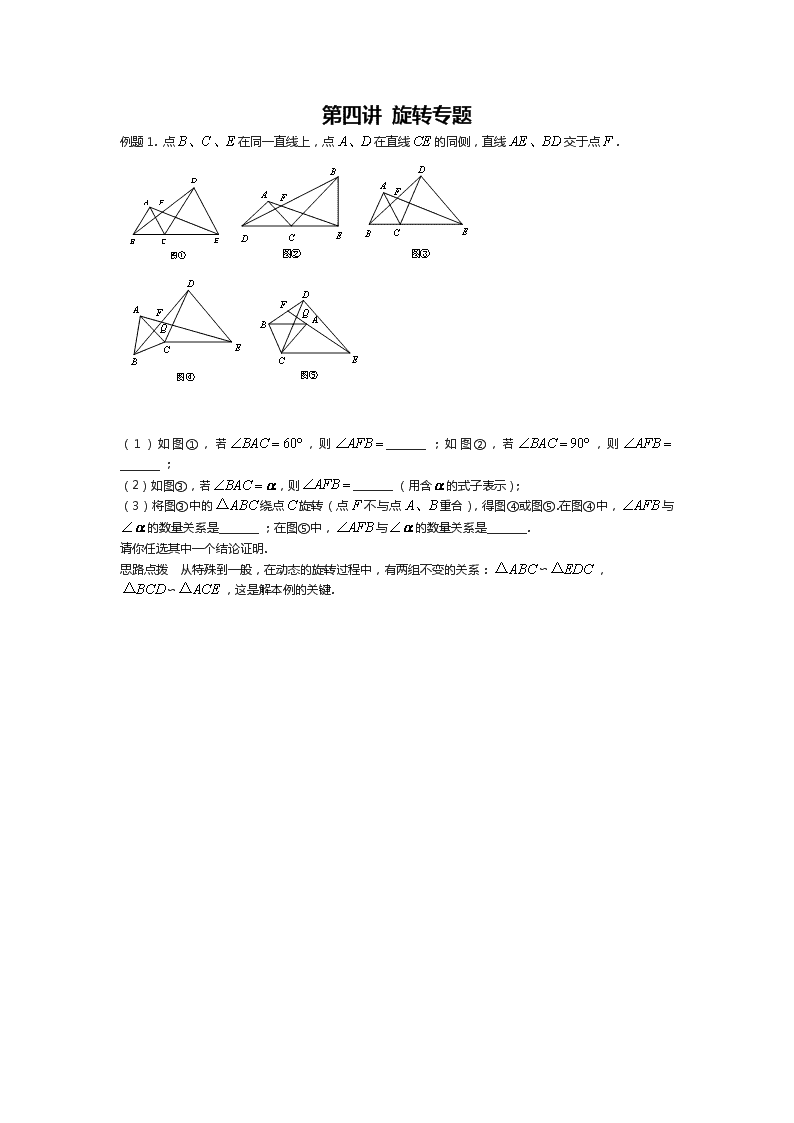
第四讲 旋转专题 例题1. 点在同一直线上，点在直线的同侧，直线交于点.‎ ‎（1）如图①，若，则________；如图②，若，则________；‎ ‎（2）如图③，若，则________（用含的式子表示）；‎ ‎（3）将图③中的绕点旋转（点不与点重合），得图④或图⑤.在图④中，与的数量关系是________；在图⑤中，与的数量关系是________.‎ 请你任选其中一个结论证明.‎ 思路点拨 从特殊到一般，在动态的旋转过程中，有两组不变的关系：∽，‎ ‎∽，这是解本例的关键.‎ 例2.如图1，是等腰直角三角形，四边形是正方形，、分别在、边上，此时，成立．‎ ‎（1）当正方形绕点逆时针旋转（）时，如图2，成立吗？若成立，请证明；若不成立，请说明理由．‎ ‎（2）当正方形绕点逆时针旋转时，如图3，延长交于点．‎ ‎①求证：；‎ ‎②当，时，求线段的长．‎ 例3. 在正方形的边上任取一点，作交于点，取的中点，连接，如图①，易证且.‎ ‎（1）将绕点逆时针旋转，如图②，则线段和有怎样的数量关系和位置关系？请直接写出你的猜想.‎ ‎（2）将绕点逆时针旋转，如图③，则线段和有怎样的数量关系和位置关系？请写出你的猜想，并加以证明.‎ 例4. 如图①，在等边中，点是边的中点，点是线段上的动点（点与点不重合），连接.将绕点按顺时针方向旋转角（），得到，连接，射线分别交射线、射线于点.‎ ‎（1）如图①，当时，在角变化过程中，与始终存在________关系（填“相似”或“全等”），并说明理由；‎ ‎（2）如图②，设.当时，有角变化过程中，是否存在与全等？若存在，求出与之间的数量关系；若不存在，请说明理.‎ ‎（3）如图③，当时，点与点重合.已知，设，的面积为，求关于的函数关系式.‎ 例5. 将两块全等的直角三角形纸片△ABC和△DEF叠放在一起，其中∠ACB=∠E=90°，BC=DE=6，AC=FE=8，点D与边AB的中点重合，将△DEF绕着点D旋转．‎ ‎（1）如图1，如果∠EDF的边DE经过点C，另一边DF与边AC交于点G，求GC的长；‎ ‎（2）如图2，如果∠EDF的边DF、DE分别交边BC于点M、N，设CN=x、BM=y，求y关于x的函数解析式，并求它的定义域；‎ ‎（3）如图3，如果∠EDF的边DF、DE分别交边AC于点M、N，如果△DMN是等腰三角形，求AN的值．‎ 例6. 已知，直角三角形ABC中，∠C=90°，点D、E分别是边AC、AB的中点，BC=6．‎ ‎（1）如图1，动点P从点E出发，沿直线DE方向向右运动，则当EP=　　时，四边形BCDP是矩形；‎ ‎（2）将点B绕点E逆时针旋转．‎ ‎①如图2，旋转到点F处，连接AF、BF、EF．设∠BEF=α°，求证：△ABF是直角三角形；‎ ‎②如图3，旋转到点G处，连接DG、EG．已知∠BEG=90°，求△DEG的面积．‎ 例7.如图1，点O为正方形ABCD的中心．‎ ‎（1）将线段OE绕点O逆时针方向旋转90°,点E的对应点为点F，连结EF，AE，BF，请依题意补全图1；‎ ‎（2）根据图1中补全的图形，猜想并证明AE与BF的关系；‎ ‎（3）如图2，点G是OA中点，△EGF是等腰直角三角形，H是EF的中点，∠EGF=90°，AB=2‎2‎，GE=2，△EGF绕G点逆时针方向旋转α角度，请直接写出旋转过程中BH的最大值．‎ 例8. 如图1，在△ABC中，CA=CB，∠ACB=90°，D是△ABC内部一点，∠ADC=135°，将线段CD绕点C逆时针旋转90°得到线段CE，连接DE．‎ ‎（1）①依题意补全图形；②请判断∠ADC和∠CDE之间的数量关系，并直接写出答案．‎ ‎（2）在（1）的条件下，连接BE，过点C作CM⊥DE，请判断线段CM，AE和BE之间的数量关系，并说明理由．‎ ‎（3）如图2，在正方形ABCD中，AB=‎2‎，如果PD=1，∠BPD=90°，请直接写出点A到BP的距离．‎ 例9.如图1，在△ABC中，AB=AC，射线BP从BA所在位置开始绕点B顺时针旋转，旋转角为α（0°＜α＜180°）‎ ‎（1）当∠BAC=60°时，将BP旋转到图2位置，点D在射线BP上．若∠CDP=120°，则∠ACD　　∠ABD（填“＞”、“=”、“＜”），线段BD、CD与AD之间的数量关系是　　；‎ ‎（2）当∠BAC=120°时，将BP旋转到图3位置，点D在射线BP上，若∠CDP=60°，求证：BD﹣CD=‎3‎AD；‎ ‎（3）将图3中的BP继续旋转，当30°＜α＜180°时，点D是直线BP上一点（点P不在线段BD上），若∠CDP=120°，请直接写出线段BD、CD与AD之间的数量关系（不必证明）．‎ 例10.已知：点D是等腰直角三角形ABC斜边BC所在直线上一点（不与点B重合），连接AD．‎ ‎（1）如图1，当点D在线段BC上时，将线段AD绕点A逆时针方向旋转90°得到线段AE，连接CE．求证：BD=CE，BD⊥CE．‎ ‎（2）如图2，当点D在线段BC延长线上时，探究AD、BD、CD三条线段之间的数量关系，写出结论并说明理由；‎ ‎（3）若BD=‎3‎CD，直接写出∠BAD的度数．‎ 例11.如图1，在△ABC中，∠ACB=90°，AC=BC，∠EAC=90°，点M为射线AE上任意一点（不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，直线NB分别交直线CM、射线AE于点F、D．‎ ‎（1）直接写出∠NDE的度数；‎ ‎（2）如图2、图3，当∠EAC为锐角或钝角时，其他条件不变，（1）中的结论是否发生变化？如果不变，选取其中一种情况加以证明；如果变化，请说明理由；‎ ‎（3）如图4，若∠EAC=15°，∠ACM=60°，直线CM与AB交于G，BD=‎6‎‎+‎‎2‎‎2‎，其他条件不变，求线段AM的长．‎ 例12.已知正方形ABCD和正方形EBGF共顶点B，连AF，H为AF的中点，连EH，正方形EBGF绕点B旋转．‎ ‎（1）如图1，当F点落在BC上时，求证：EH=‎1‎‎2‎FC；‎ ‎（2）如图2，当点E落在BC上时，连BH，若AB=5，BG=2，求BH的长；‎ ‎（3）当正方形EBGF绕点B旋转到如图3的位置时，求EHCF的值．‎ 例13.已知正方形和等腰，，，按图甲放置，使点在上，取 的中点，连接．‎ ‎⑴ 探索的数量关系和位置关系，并说明理由；‎ ‎⑵ 将图甲中绕点顺时针旋转得图乙，连接，取的中点，问⑴中的结论是否成立？并说明理由；‎ ‎⑶ 将图甲中绕点转动任意角度（旋转角在到之间）得图丙，连接，取的中点，问⑴中的结论是否成立，请说明理由．‎ 例14.如图，△ABC中，点D在AC上，点E在BC上，且DE∥AB，将△CDE绕点C按顺时针方向旋转得到△CD′E′（使∠BCE′＜180°），连接AD′、BE′，设直线BE′与AC、AD′分别交于点O、E．‎ ‎（1）若△ABC为等边三角形，则AD'‎BE'‎的值为1，求∠AFB的度数；‎ ‎（2）若△ABC满足∠ACB=60°，AC=‎3‎，BC=‎2‎，‎ ‎①求AD'‎BE'‎的值和∠AFB的度数；‎ ‎②若E为BC的中点，求△OBC面积的最大值．‎ 例15.已知，在中，．过点的直线从与边重合的位置开始绕点按顺时针方向旋转角，直线交边于点（点不与点、点重合），的边始终在直线上（点在点的上方），且，连接．‎ ‎（1）当时，‎ ‎①如图a，当时，的度数为___________；‎ ‎②如图b，当时，①中的结论是否发生变化？说明理由；‎ ‎（2）如图c，当时，请直接写出与之间的数量关系，不必证明．‎ 例16.两个大小相同且含30°角的三角板和如图①摆放，使直角顶点重合．将图①中绕点逆时针旋转30°得到图②，点、分别是、与的交点，点是与的交点．‎ ‎（1）不添加辅助线，写出图②中所有与全等的三角形；‎ ‎（2）将图②中的绕点逆时针旋转45°得，点、、对应点分别为、、，如图③．探究线段与之间的数量关系，并写出推理过程；‎ ‎（3）在（2）的条件下，若与交于点，求证：．‎ 例17.如图1，在中，点为边中点，直线绕顶点旋转，若点，在直线的异侧，⊥直线于点．⊥直线于点，连接，．‎ ‎（1）延长交于点（如图2）．‎ ‎①求证：；‎ ‎②求证：；‎ ‎（2）若直线绕点旋转到图3的位置时，点，在直线的同侧，其它条件不变，此时还成立吗？若成立，请给予证明；若不成立，请说明理由；‎ ‎（3）若直线绕点旋转到与边平行的位置时，其它条件不变，请直接判断四边形的形状及此时还成立吗？不必说明理由．‎ 例18.已知是等腰直角三角形，，是边上一动点（、两点除外），将绕点按逆时针方向旋转角得到，其中点是点的对应点，点是点的对应点．‎ ‎（1）如图1，当时，是边上一点，且，连接．求证：；‎ ‎（2）如图2，当时，与相交于点．‎ ‎①当点与点、不重合时，连接，求的度数；‎ ‎②设为边的中点，当从变化到时，求点运动的路径长．‎ 例19.已知正方形ABCD的边长为4，一个以点A为顶点的45°角绕点A旋转，角的两边分别与边BC、DC的延长线交于点E、F，连接EF．设CE=a，CF=b．‎ ‎（1）如图1，当∠EAF被对角线AC平分时，求a、b的值；‎ ‎（2）当△AEF是直角三角形时，求a、b的值；‎ ‎（3）如图3，探索∠EAF绕点A旋转的过程中a、b满足的关系式，并说明理由．‎ 例20. 已知：点P是平行四边形ABCD对角线AC所在直线上的一个动点（点Ｐ不与点A、C重合），分别过点A、C向直线BP作垂线，垂足分别为点E、F，点O为AC的中点.‎ ‎（1）当点P与点O重合时如图1，易证OE=OF（不需证明）.‎ ‎（2）直线BP绕点B逆时针方向旋转，当∠OFE=30°时，如图2、图3的位置，猜想线段CF、AE、OE之间有怎样的数量关系？请写出你对图2、图3的猜想，并选择一种情况给予证明.‎ ‎ ‎ ‎ ‎ ‎ ‎ 例21. 在△ABC中，AB=AC，∠A=60°，点D是线段BC的中点，∠EDF=120°，DE与线段AB相交于点E．DF与线段AC（或AC的延长线）相交于点F．‎ ‎（1）如图1，若DF⊥AC，垂足为F，AB=4，求BE的长；‎ ‎（2）如图2，将（1）中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F．求证：BE+CF=AB；‎ ‎（3）如图3，将（2）中的∠EDF继续绕点D顺时针旋转一定的角度，使DF与线段AC的延长线相交于点F，作DN⊥AC于点N，若DN⊥AC于点N，若DN=FN，求证：BE+CF=（BE﹣CF）．‎ 例22. 在△ABC中，AB=BC=2，∠ABC=90°，BD为斜边AC上的中线，将△ABD绕点D顺时针旋转α（0°＜α＜180°）得到△EFD，其中点A的对应点为点E，点B的对应点为点F．BE与FC相交于点H．‎ ‎（1）如图1，直接写出BE与FC的数量关系： ；‎ ‎（2）如图2，M、N分别为EF、BC的中点．求证：MN=；‎ ‎（3）连接BF，CE，如图3，直接写出在此旋转过程中，线段BF、CE与AC之间的数量关系： ．‎ 例23.如图1，在菱形ABCD中，AC=6，BD=6，AC，BD相交于点O． ‎ ‎（1）求边AB的长；‎ ‎（2）如图2，将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处，绕点A左右旋转，其中三角板60°角的两边分别于边BC，CD相交于E，F，连接EF与AC相交于点G．‎ ‎①判断△AEF是哪一种特殊三角形，并说明理由；‎ ‎②旋转过程中是否存在线段EF最短，若存在，求出最小值，若不存在，请说明理由．‎ 例24.在Rt△ABC中，∠A=90°，AC=AB=4，D，E分别是边AB，AC的中点，若等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1，设旋转角为α（0＜α≤180°），记直线BD1与CE1的交点为P．‎ ‎（1）如图1，当α=90°时，线段BD1的长等于 ，线段CE1的长等于 ；（直接填写结果）‎ ‎（2）如图2，当α=135°时，求证：BD1=CE1，且BD1⊥CE1；‎ ‎（3）求点P到AB所在直线的距离的最大值．（直接写出结果）‎ 例25.在正方形ABCD中，对角线AC与BD交于点O；在Rt△PMN中，∠MPN=90°．‎ ‎（1）如图1，若点P与点O重合且PM⊥AD、PN⊥AB，分别交AD、AB于点E、F，请直接写出PE与PF的数量关系；‎ ‎（2）将图1中的Rt△PMN绕点O顺时针旋转角度α（0°＜α＜45°）．‎ ‎①如图2，在旋转过程中（1）中的结论依然成立吗？若成立，请证明；若不成立，请说明理由；‎ ‎②如图2，在旋转过程中，当∠DOM=15°时，连接EF，若正方形的边长为2，请直接写出线段EF的长；‎ ‎③如图3，旋转后，若Rt△PMN的顶点P在线段OB上移动（不与点O、B重合），当BD=3BP时，猜想此时PE与PF的数量关系，并给出证明；当BD=m•BP时，请直接写出PE与PF的数量关系．‎ 例26.如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，将∠QPN绕点P旋转，旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C，D不重合）．‎ ‎（1）如图①，当α=90°时，DE，DF，AD之间满足的数量关系是 ；‎ ‎（2）如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为DE+DF=AD，请给出证明；‎ ‎（3）在（2）的条件下，若旋转过程中∠QPN的边PQ与射线AD交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．‎ 例27. 如图1，在菱形ABCD和菱形BEFG中，点A、B、E在同一条直线上，P是线段DF的中点，连接PG，PC．若∠ABC=∠BEF=60°．‎ ‎（1）请直接写出线段PG与PC的位置关系及的值．‎ ‎（2）若将图1中的菱形BEFG饶点B顺时针旋转，使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上，原问题中的其他条件不变，如图2．那么你在（1）中得到的结论是否发生变化？若没变化，直接写出结论，若有变化，写出变化的结果．‎ ‎（3）在图1中，若∠ABC=∠BEF=2α（0°＜α＜90°），将菱形BEFG饶点B顺时针旋转任意角度，原问题中的其他条件不变，请直接写出的值（用含α的式子表示）．‎ 例28.如图①所示，在和中，AB=AC,AD=AE,，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．‎ ‎（1）求证：①BE=CD；②△AMN是等腰三角形；‎ ‎（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；‎ ‎（3）在（2）的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．‎ 例29.如图1，和都是等腰直角三角形，，点在线段上，点在线段上．‎ ‎（1）请直接写出线段与线段的关系：_____________；‎ ‎（2）如图2，将图1中的绕点顺时针旋转角（），‎ ‎①（1）中的结论是否成立？若成立，请利用图2证明；若不成立，请说明理由；‎ ‎②当时，探究在旋转的过程中，是否存在这样的角，使以、、、四点为顶点的四边形是平行四边形？若存在，请直接写出角的度数；若不存在，请说明理由．‎ 例30.如图，在中，.将直角三角板的直角顶点放在线段的中点上，以点为旋转中心，转动三角板并使三角板的两直角边分别与相交于点，连，交于点.‎ ‎（1）求证：；‎ ‎（2）设线段的长为，的面积为，求与的函数关系式；‎ ‎（3）当三角板旋转到时，求的长.‎ 例31. 如图①，中，，于点，点在上，且，连结．‎ ‎（1）求证：；‎ ‎（2）将绕点旋转，得到（点，分别与点，对应），连接．‎ ‎①如图②，当点落在上时，（不与重合），若，，求的长；‎ ‎②如图③，当是由绕点逆时针旋转得到时，设射线与相交于点，连接，试探究线段与之间满足的等量关系，并说明理由．‎ 例32. 如图1，在四边形中，点、分别是、的中点，过点作的垂线，过点作的垂线，两垂线交于点，连接、、、，且．‎ ‎（1）求证：；‎ ‎（2）求证：；‎ ‎（3）如图2，若、所在直线互相垂直，求的值．‎ 例33. 已知是等腰直角三角形，，，，，连接，点是的中点．‎ ‎（1）如图1，若点在边上，连接，当时，求的长；‎ ‎（2）如图2，若点在的内部，连接，点是中点，连接，，求证：；‎ ‎（3）如图3，将图2中的绕点逆时针旋转，使，连接，点是中点，连接，探索的值并直接写出结果．‎ 例34. 已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．‎ ‎（1）求证：EG=CG；‎ ‎（2）将图①中△BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；‎ ‎（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．‎ 例35. 如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．‎ ‎（1）求证：△AMB≌△ENB；‎ ‎（2）①当M点在何处时，AM+CM的值最小；‎ ‎②当M点在何处时，AM+BM+CM的值最小，并说明理由；‎ ‎（3）当AM+BM+CM的最小值为时，求正方形的边长．‎ 例36. 如图甲，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．‎ 解答下列问题：‎ ‎（1）如果AB=AC，∠BAC=90°，‎ ‎①当点D在线段BC上时（与点B不重合），如图乙，线段CF，BD之间的位置关系为　　，数量关系为　　．‎ ‎②当点D在线段BC的延长线时，如图丙，①中的结论是否仍然成立，为什么？‎ ‎（2）如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．‎ 试探究：当△ABC满足一个什么条件时，CF⊥BC（点C，F重合除外）画出相应图形，并说明理由．（画图不写作法）‎ ‎（3）若AC=4，BC=3，在（2）的条件下，设正方形ADEF的边DE与线段CF相交于点P，求线段CP长的最大值．‎ 例37. 已知：在△ABC中，BC=a，AC=b，以AB为边作等边三角形ABD．探究下列问题：‎ ‎（1）如图1，当点D与点C位于直线AB的两侧时，a=b=3，且∠ACB=60°，则CD=　　；‎ ‎（2）如图2，当点D与点C位于直线AB的同侧时，a=b=6，且∠ACB=90°，则CD=　　；‎ ‎（3）如图3，当∠ACB变化，且点D与点C位于直线AB的两侧时，求 CD的最大值及相应的∠ACB的度数．‎ 例38. 在△ABC中，点D在AC上，点E在BC上，且DE∥AB，将△CDE绕点C按顺时针方向旋转得到△CD’E’（使∠BCE′＜180°），连接AD′、BE′，设直线BE′与AC交于点O．‎ ‎（1）如图1，当AC=BC时，AD′：BE′的值为　　；‎ ‎（2）如图2，当AC=5，BC=4时，求AD′：BE′的值；‎ ‎（3）在（2）的条件下，若∠ACB=60°，且E为BC的中点，求△OAB面积的最小值．‎ 例39. 将绕点按逆时针方向旋转度，并使各边长变为原来的倍，得，即如图①，.我们将这种变换记为[，].‎ (1) 如图①，对作变换[60°，]得，则_ ；直线与直线所夹的锐角为 ＿ 度．‎ (2) 如图②，中，，对作变换[，]得，使点，，在同一直线上，且四边形为矩形，求和的值。‎ (3) 如图③，中，，，对作变换[，]得，使点，，在同一直线上，且四边形为平行四边形，求和的值。‎ 例40. 已知：将一副三角板（和）如图①摆放，点、、、在一条直线上， ‎ ‎ 且是的中点，将绕点顺时针方向旋转角)，在旋转过程中，直线 ‎ ，相交与点，直线、相交与点，分别过点、作直线的垂线，垂足 ‎ 为、。‎ ‎ （1）当时（如图②），求证：；‎ ‎ （2）当时（如图③），(1)中的结论是否成立？请写出你的结论并说明理由；‎ ‎ （3）当0°<时（1）中的结论是否成立？请写出你的结论，并根据图④说明理由 ‎ ‎ 例41. 已知：如图①，在面积为3的正方形中，、分别是和边上的两点，‎ ‎ 垂足为点，且.‎ ‎ （1）求证: ；‎ ‎ （2）求出和重叠部分（）的面积 ‎ （3）现将绕点顺时针方向旋转到（如图②），使点落在边上的点处，‎ ‎ 问在旋转前后与重叠部分的面积是否发生了变化？请说明理由。‎ 例42. 在中，的两边交边于两点，将 ‎ ‎ 绕点旋转．‎ ‎ ⑴ 画出绕点顺时针旋转后的；‎ ‎ ⑵ 在⑴中，若，求证：； ‎ ‎ ⑶ 在⑵的条件下，若，直接写出的长．‎ 例43. 如图1，将矩形绕点顺时针旋转至矩形，使点正好落在上的 ‎ ‎ 点处，连．‎ ‎ ⑴ 注证：；‎ ‎ ⑵ 如图2，连交于，点为的中点，连，试探究与的数量 ‎ ‎ 关系，并证明你的结论；‎ ‎ ⑶ 若，直接写出的长 ．‎ 例44. 如图，四边形是正方形，是等边三角形，为对角线（不含点）上任意一 点， ‎ ‎ 将绕点逆时针旋转得到，连接、、.‎ ‎⑴ 求证：；‎ ‎⑵ ①当点在何处时，的值最小；‎ ‎②当点在何处时，的值最小，并说明理由；‎ ‎⑶ 当的最小值为时，求正方形的边长.‎ E A D B C N M 例45. 已知：，以为一边作正方形，使两点落在直线AB的两侧.‎ ‎⑴ 如图，当时，求及的长；‎ ‎⑵ 当变化，且其它条件不变时，求的最大值，及相应的大小.‎ ‎ 例46.如图①，在Rt△ABC中，∠BAC=90°，AB=AC=‎2‎‎3‎，D、E两点分别在AC、BC上，且DE∥AB，CD=‎2‎‎2‎．将△CDE绕点C顺时针旋转，得到△CD′E′（如图②，点D′、E′分别与点D、E对应），点E′在AB上，D′E′与AC相交于点M．‎ ‎（1）求∠ACE′的度数；‎ ‎（2）求证：四边形ABCD′是梯形；‎ ‎（3）求△AD′M的面积．‎