2007年中考数学湖北省宜昌市试卷 15页

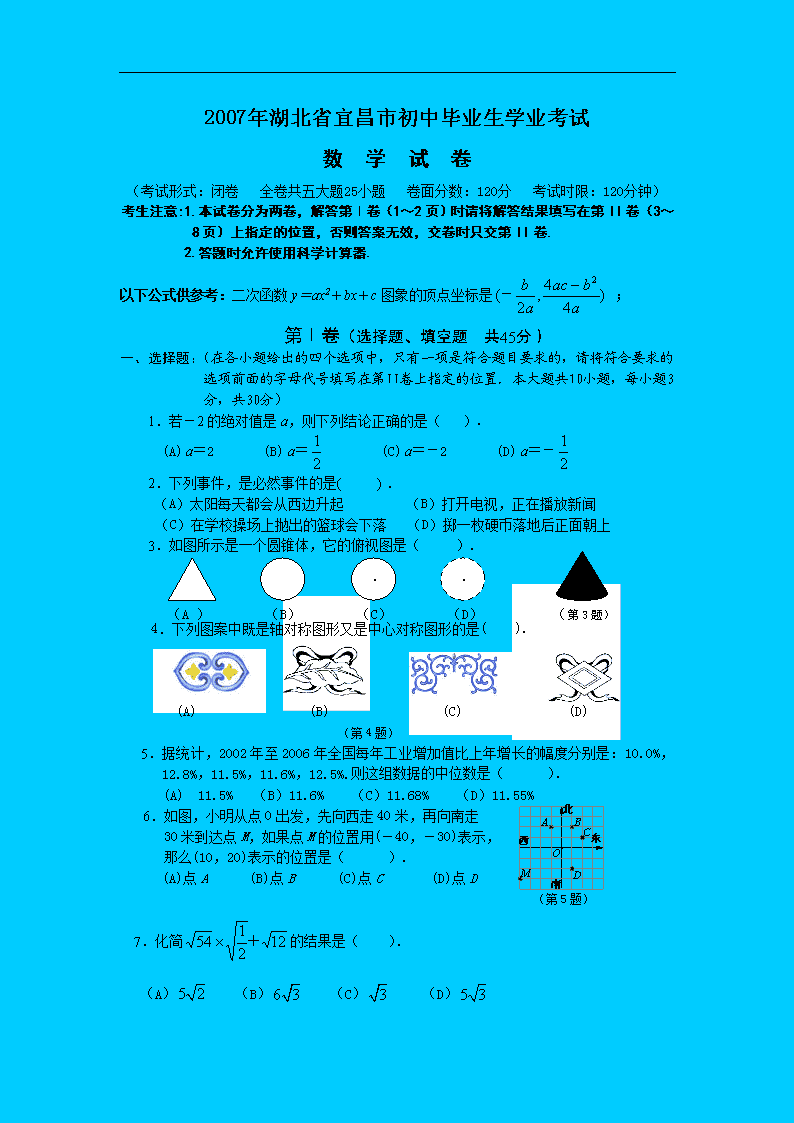
‎2007年湖北省宜昌市初中毕业生学业考试 数 学 试 卷 ‎（考试形式：闭卷 全卷共五大题25小题 卷面分数：120分 考试时限：120分钟）‎ 考生注意:1.本试卷分为两卷，解答第Ⅰ卷（1～2页）时请将解答结果填写在第II卷（3～8页）上指定的位置，否则答案无效，交卷时只交第II卷.‎ ‎ 2.答题时允许使用科学计算器.‎ 以下公式供参考：二次函数y＝ax2＋bx＋c图象的顶点坐标是 ； ‎ 第Ⅰ卷（选择题、填空题 共45分）‎ 一、选择题：（在各小题给出的四个选项中，只有一项是符合题目要求的，请将符合要求的选项前面的字母代号填写在第II卷上指定的位置. 本大题共10小题，每小题3分，共30分）‎ ‎1．若－2的绝对值是a，则下列结论正确的是（ ）.‎ ‎(A) a＝2 (B) a＝ (C) a＝－2 (D) a＝－ ‎ ‎2．下列事件，是必然事件的是( ) . ‎ ‎（A）太阳每天都会从西边升起 （B）打开电视，正在播放新闻 ‎（C）在学校操场上抛出的篮球会下落 （D）掷一枚硬币落地后正面朝上 ‎ ‎·‎ ‎·‎ ‎（A ） （B） （C） （D） （第3题）‎ ‎3．如图所示是一个圆锥体，它的俯视图是（ ）.‎ ‎ 4．下列图案中既是轴对称图形又是中心对称图形的是( ). ‎ ‎ ‎ ‎ ‎ ‎(A) (B) (C) (D)‎ ‎（第4题）‎ ‎5．据统计，2002年至2006年全国每年工业增加值比上年增长的幅度分别是：10.0%，12.8%，11.5%，11.6%，12.5%.则这组数据的中位数是（ ）．‎ ‎ (A) 11.5% （B）11.6% （C）11.68% （D）11.55% ‎ ‎6．如图，小明从点O出发，先向西走‎40米，再向南走 ‎30米到达点M，如果点M的位置用(－40，－30)表示，‎ 那么(10，20)表示的位置是（ ）.‎ ‎(A)点A (B)点B (C)点C (D)点D ‎ ‎（第5题）‎ ‎7．化简的结果是（ ）．‎ ‎（A） （B） （C） （D）‎ E D B C A F ‎（第8题）‎ ‎8. 如图，四边形ABCD是矩形，F是AD上一点，E是CB延长线上一点，且四边形AECF是等腰梯形．下列结论中不一定正确的是（ ）．‎ ‎ （A）AE=FC （B）AD=BC ‎ ‎（C）∠AEB=∠CFD （D）BE=AF ‎9.一种细胞的直径约为1.56×10－‎6 米，那么它的一百万倍相当于（ ）．‎ ‎（A）玻璃跳棋棋子的直径 （B）数学课本的宽度 ‎（C）初中学生小丽的身高 （D）五层楼房的高度 O x y ‎（第10题）‎ ‎10．反比例函数与二次函数在同一平面直角坐标系中的大致图象 如图所示，它们的解析式可能分别是（ ）．‎ ‎（A）y=，y=kx2-x （B）y=，y=kx2+x ‎ ‎（C）y=-，y=kx2+x （D）y=-，y=-kx2-x ‎ 二、填空题：（本大题共5小题，每小题3分，计15分）‎ ‎11．一电冰箱冷冻室的温度是‎-18℃‎，冷藏室的温度是‎5℃‎，该电冰箱冷藏室的温度比冷冻室的温度高 ℃.‎ ‎12．夷陵长江大桥为三塔斜拉桥．如图，中塔左右两边所挂的 最长钢索AB=AC,塔柱底端D与点B间的距离是‎228米，‎ 则BC的长是 米．‎ ‎（第12题）‎ ‎13．随机掷一枚均匀的骰子，点数小于3的概率是 .‎ ‎14．两个圆的半径分别为3和4，圆心之间的距离是5，这两个圆的位置关系是　　　 . ‎ ‎15．1766年德国人提丢斯发现，太阳系中的行星到太阳的距离遵循一定的规律，如下表所示：‎ 颗 次 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎…‎ 行星名称 水星 金星 地球 火星 小行星 木星 ‎…‎ 距离（天文单位）‎ ‎0.4‎ ‎0.7‎ ‎1‎ ‎1.6‎ ‎2.8‎ ‎5.2‎ ‎…‎ ‎0.4‎ ‎0.4+0.3‎ ‎0.4+0.6‎ ‎0.4+1.2‎ ‎0.4+2.4‎ ‎…‎ ‎…‎ ‎ 那么第7颗行星到太阳的距离是 天文单位.‎ ‎2007年湖北省宜昌市初中毕业生学业考试 数学试卷 题 号 一 二 三 四 五 总分 得 分 第Ⅱ卷 （解答题 共75分）‎ 一、选择题答案栏：（请将第I卷中选择题的答案填写在下表中）‎ 得分 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 评卷人 答 案 二、填空题答案栏：（请将第I卷中填空题的答案填写在下表中）‎ 得分 题 号 ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 评卷人 答 案 得 分 三、解答题：（本大题共4小题，每小题6分，共24分）‎ 评卷人 ‎16．请将式子：×（1＋）化简后，再从0，1，2三个数中选择一个你喜欢且使原式有意义的x的值带入求值.‎ E D C B A G ‎（第17题）‎ ‎17．如图，G是线段AB上一点，AC和DG相交于点E.请先作出∠ABC的平分线BF，交AC于点F；（尺规作图，保留作图痕迹，不写作法与证明）然后证明当：AD∥BC，AD=BC，∠ABC=2∠ADG时， DE=BF.‎ ‎{‎ ‎18. 解下列不等式组： ‎ ‎ x+5≥2x+2 ‎ ‎ 2+x＞ . ‎ ‎ 19．如图，为了对我市城区省级文物保护对象－—高AC约‎42米的天然塔（清乾隆五十七年重修）进行保护性维修，工人要在塔顶A和塔底所在地面上的B处之间拉一根铁丝，在BC上的点D处测得塔顶的仰角α为43°（测倾器DE高‎1.6米，A，E，B三点在同一条直线上）．求∠BAC的度数和铁丝AB的长．（接头部分的长度忽略不计，结果精确到‎0.1米．sin43°≈0.68,tan43°≈0.93）‎ ‎ ‎ ‎ (第19题)‎ 得 分 四、解答题：（本大题共3小题，每小题7分，共21分）‎ 评卷人 ‎20. 如图，某建筑工地上一钢管的横截面是圆环形．王师傅将直尺边缘紧靠内圆，直尺与外圆交于点A，B（AB与内圆相切于点C，其中点A在直尺的零刻度处）．请观察图形，写出线段AB的长（精确到‎1cm），并根据得到的数据计算该钢管的横截面积．（结果用含π的式子表示）‎ ‎（第20题）‎ ‎21.《中学生体质健康标准》规定学生体质健康等级标准为：86分及以上为优秀；76分～85分为良好；60分～75分为及格；59分及以下为不及格．某校从九年级学生中随机抽取了10％的学生进行了体质测试，得分情况如下图．‎ ‎(1)在抽取的学生中不及格人数所占的百分比是 ；‎ ‎(2)小明按以下方法计算出抽取的学生平均得分是：(90＋78＋66＋42)÷4＝69．根据所学的统计知识判断小明的计算是否正确，若不正确，请写出正确的算式；（不必算出结果）‎ 良好 ‎26%‎ 等级 均分 ‎(3)若不及格学生的总分恰好等于某一个良好等级学生的分数，请估算出该校九年级学生中优秀等级的人数．‎ ‎(第21题)‎ ‎22．2007年5月，第五届中国宜昌长江三峡国际龙舟拉力赛在黄陵庙揭开比赛帷幕．20日上午9时，参赛龙舟从黄陵庙同时出发．其中甲、乙两队在比赛时，路程y（千米）与时间x（小时）的函数关系如图所示．甲队在上午11时30分到达终点黄柏河港．‎ ‎（1）哪个队先到达终点？乙队何时追上甲队？‎ ‎（2）在比赛过程中，甲、乙两队何时相距最远？ ‎ ‎（第22题）‎ ‎ 得分 ‎23题 ‎24题 ‎25题 五、解答题：（本大题共3小题，每小题10分，共30分）‎ 评卷人 ‎23. 椐报道，2007年“五一”黄金周宜昌市共接待游客约80万人，旅游总收入约2.56亿元.其中县区接待的游客人数占全市接待的游客人数的60%，而游客人均旅游消费（旅游总收入÷旅游总人数）比城区接待的游客人均旅游消费少50元.‎ ‎（1）2007年“五一”黄金周，宜昌市城区与县区的旅游收入分别是多少万元？‎ ‎（2）预计2008年“五一”黄金周与2007年同期相比，全市旅游总收入增长的百分数是游客人均旅游消费增长百分数的2.59倍，游客人数增长的百分数是游客人均旅游消费增长百分数的1.5倍.请估计2008年“五一”黄金周全市的旅游总收入是多少亿元？（保留3个有效数字）‎ ‎24.如图1，在△ABC中，AB＝BC＝5，AC=6. △ECD是△ABC沿BC方向平移得到的，连接AE.AC和BE相交于点O.‎ ‎（1）判断四边形ABCE是怎样的四边形，说明理由； ‎ ‎（2）如图2，P是线段BC上一动点（图2），（不与点B、C重合），连接PO并延长交线段AB于点Q，QR⊥BD，垂足为点R.‎ ①四边形PQED的面积是否随点P的运动而发生变化？若变化，请说明理由；若不变，求出四边形PQED的面积；‎ ②当线段BP的长为何值时，△PQR与△BOC相似？‎ C O E D B A ‎（备用图）‎ ‎1‎ C O E D B A R P Q C O E D B A ‎（第24题图2）‎ ‎（第24题图1）‎ ‎1‎ ‎ ‎ ‎25.如图1，点A是直线y＝kx（k＞0，且k为常数）上一动点，以A为顶点的抛物线y＝(x－h)2＋m交直线y＝x于另一点E，交 y 轴于点F，抛物线的对称轴交x轴于点B，交直线EF于点C.（点A,E,F两两不重合）‎ ‎(1)请写出h与m之间的关系；（用含的k式子表示）‎ ‎(2)当点A运动到使EF与x轴平行时(如图2)，求线段AC与OF的比值；‎ ‎(3)当点A运动到使点F的位置最低时(如图3)，求线段AC与OF的比值.‎ ‎ ‎ ‎（第25题图1）‎ ‎（第25题图2）‎ 祝贺你！‎ 再检查一遍吧!‎ ‎（第25题图3）‎ ‎2007年湖北省宜昌市初中学业考试 数学试卷参考答案及评分说明 ‎（一）阅卷评分说明 ‎1.正式阅卷前先进行试评，在试评中认真阅读参考答案，明确评分标准，不得随意拔高或降低评分标准. 试评的试卷必须在阅卷后期全部予以复查，防止阅卷前后期评分标准宽严不一致.‎ ‎2.评分方式为分小题分步累计评分，解答过程的某一步骤发生笔误，只要不降低后继部分的难度，而后继部分再无新的错误，后继部分可评应得分数的50%；若是几个相对独立的得分点，其中一处错误不影响其它得分点的评分.‎ ‎3.最小记分单位为1分，不得将评分标准细化至1分以下（即不得记小数分）.‎ ‎4.解答题题头一律记该题的实际得分，不得用记负分的方式记分. 对解题中的错误须用红笔标出，并继续评分，直至将解题过程评阅完毕，并在最后得分点处标上该题实际得分.‎ ‎5.本参考答案只给出一种或几种解法，凡有其它正确解法都应参照本评分说明分步确定得分点，并同样实行分小题分步累计评分.‎ ‎6.合理精简解题步骤者，其简化的解题过程不影响评分.‎ ‎（二）参考答案及评分标准 一、选择题:（每小题3分，共30分）‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答 案 A C ‎ C A B ‎ B D ‎ D C B 二、填空题:（每小题3分，共15分）‎ 题 号 ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 答 案 ‎23‎ 相交 ‎456‎ ‎10‎ 三、解答题:（每小题6分，共24分）‎ ‎16．解：原式=×(1+)(1分)=(x+1()(2分)=x+x+1(3分)=x+2(4分)‎ 方法一：当x=0时（5分），原式=2(6分)；‎ 方法二：当x=2时（5分），原式=4(6分). （注：化简正确，取x＝1带入计算全题评4分；不化简直接求值结果正确全题评2分）‎ ‎17.解：（1）以B为圆心、适当长为半径画弧，交AB、BC于M、N两点（1分），分别以M、N为圆心、大于MN长为半径画弧，两弧相交于点P（2分），过B、P作射线BF交AC于F（3分）（注：没有作出射线BF与AC的交点并表明标明F扣1分）；‎ ‎（2）证明：∵AD∥BC，∴∠DAC=∠C（1分），‎ 又∵BF平分∠ABC，且∠ABC=2∠ADG，∴∠D=∠BFC（2分），‎ 又∵AD=BC，∴△ADE≌△CBF，∴DE=BF（3分）.‎ ‎18.解：由①得：-x≥-3（1分），x≤3（2分）；‎ 由②得：6＋2x＞4（3分），x＞-1（4分），‎ ‎∴原不等式组的解集是：-1＜x≤3（6分）.‎ ‎19、解：∵BC∥EF，∴∠AEF＝∠B＝43°，(1分)‎ ‎∵∠ACB＝90°，∴∠BAC＝90°－43°＝47°，(2分)‎ 在Rt△ABC中，sinB＝＝，(4分)‎ ‎∴AB＝42÷sin43°≈（5分）42÷0.68≈61.8(米)，(6分)‎ 答：∠BAC＝47°，铁丝的长度是61.8米. ‎ ‎（结果不按要求取近似值，或取值错误扣1分） ‎ 四、解答题:（每小题7分，共21分）‎ ‎20. 解：AB＝24cm(1分)； 连接OC，OA(2分)‎ ‎∵AB与内圆相切与点C ∴OC⊥AB(3分) ∴AC＝BC＝12cm(4分)‎ ‎∴横截面积为：πAO2－πOC2＝π(AO2－OC2) (5分)‎ ‎∵在Rt△ACO中，AO2－OC2＝AC2 ‎ ‎∴横截面积＝πAC2 (6分)＝144π(cm2) (7分)‎ ‎（注：读数不按要求精确或者读数错误扣1分；最后结果中无单位扣1分）‎ ‎21、解：(1)4%(1分)； (2)不正确 ，(1分)‎ 正确的算法：90×18%＋78×26%＋66×52%＋42×4%(2分)‎ ‎(3)方法一：因为一个良好等级学生分数为76～85分，而不及格学生均分为42分，‎ 由此可以知道不及格学生仅有2人（将一个良好等级的分数当成78分估算出此结果也可），(2分) ‎ 抽取优秀等级学生人数是：2÷4%×18%=9人，(3分)‎ 九年级优秀人数约为：9÷10%＝90人(4分)‎ 方法二：设不及格的人数为x人，则76≤42x≤85，（1分）1.8≤x≤2.0，x＝2（2分），‎ 下同上；‎ 方法三：设九年级总人数为x人，则76≤42×4%x×10%≤85，(1分)‎ 解得：453＜x＜505，(2分)而4%x×10%＝必须为整数，所以x＝500.(3分)‎ 九年级优秀人数大约为500×18%＝90人.(4分)‎ ‎22、解：(1)乙队先达到终点，(1分)‎ 对于乙队，x＝1时，y＝16，所以y＝16x，(2分)‎ 对于甲队，出发1小时后，设y与x关系为y＝kx＋b，‎ 将x＝1，y＝20和x＝2.5，y＝35分别代入上式得：‎ ‎ 解得：y＝10x＋10(3分) ‎ ‎（第22题）‎ 解方程组 得：x＝，即：出发1小时40分钟后（或者上午10点40分）乙队追上甲队.(4分)‎ ‎（2）1小时之内，两队相距最远距离是4千米，(1分)‎ 乙队追上甲队后，两队的距离是16x－(10x＋10)＝6x－10，当x为最大，即x＝时，6x－10最大，(2分)此时最大距离为6×－10＝3.125＜4，（也可以求出AD、CE的长度，比较其大小）所以比赛过程中，甲、乙两队在出发后1小时（或者上午10时）相距最远(3分)‎ ‎ 五、解答题：（每小题10分，共30分）‎ ‎23、解：（1）2.56亿=25600万 方法一：设城区与县区旅游收入分别为x万元和y万元，‎ 依据题意可列方程组：‎ ‎{‎ ‎ x+y=25600 （1分）‎ ‎ -=50， （2分）‎ ‎{‎ 解方程组得： x=11200(万元)‎ y=14400(万元） （3分）‎ 答：城区与县（市）区的旅游收入分别是11200万元和14400万元.（4分）‎ ‎ 方法二：设城区游客人均消费x元，则县区游客人均消费(x-50)元，‎ 依据题意可列方程：80×(1-60%)x+80×60% (x-50)＝25600，(1分)解得：x＝350（2分），‎ ‎350×80×(1-60%)＝11200（万元），25600－11200＝14400（万元）（3分）‎ 答：城区与县（市）区的旅游收入分别是11200万元和14400万元.（4分）‎ ‎（2）设2008年与2007年相比，游客人均旅游消费增长的百分数为z，则旅游总收入增长的百分数为2.59z，旅游人数增长的百分数为1.5z，（1分）‎ 依据题意可列方程： （1+z）×80（1+1.5z）=25600（1+2.59z）（3分）‎ ‎ 化简并整理得：1.5z2－0.09z=0，解得：z=0.06或z=0(舍去)（4分） ‎ ‎2008年“五一”黄金周宜昌市的旅游总收入为：‎ ‎25600（1+2.59z）=25600×（1+0.1554）=29578.24（万元）（5分）‎ ‎=2.957824（亿元）≈2.96（亿元）（6分）.(不按要求取近似值或者取近似值错误扣1分)‎ 答：估计2008年“五一”黄金周全市的旅游总收入是2.96亿元.‎ ‎24．解：（1）四边形ABCE是菱形，证明如下：‎ ‎∵△ECD是由△ABC沿BC平移得到的，∴EC∥AB，且EC＝AB，‎ ‎ ∴四边形ABCE是平行四边形，（1分）‎ 又∵AB=BC，∴四边形ABCE是菱形.（2分）‎ ‎ （2）①四边形PQED的面积不发生变化（1分），理由如下：‎ 方法一：∵ABCE是菱形，∴AC⊥BE，OC=AC=3，∵BC=5，∴BO=4，‎ ‎（第24题1）‎ P Q C H R O E D B A 过A作AH⊥BD于H，（如图1）.‎ ‎ ∵S△ABC＝BC×AH＝AC×BO，‎ 即：×5×AH＝×6×4，∴AH＝.（2分）‎ ‎【或 ∵∠AHC＝∠BOC＝90°，∠BCA公用，‎ ‎∴△AHC∽△BOC，∴AH:BO＝AC:BC，‎ 即：AH:4＝6:5，∴AH＝.（2分）】‎ 由菱形的对称性知，△PBO≌△QEO，∴BP＝QE，（3分）‎ ‎∴S四边形PQED＝（QE+PD）×QR＝（BP+PD）×AH＝BD×AH ‎ ＝×10×＝24.（4分）‎ 方法二: 由菱形的对称性知，△PBO≌△QEO，∴S△PBO＝ S△QEO，（2分）‎ ‎∵△ECD是由△ABC平移得到得，∴ED∥AC，ED＝AC＝6，‎ 又∵BE⊥AC，∴BE⊥ED，（3分）‎ ‎∴S四边形PQED＝S△QEO＋S四边形POED＝S△PBO＋S四边形POED＝S△BED ‎＝×BE×ED＝×8×6＝24.（4分）‎ ‎（第24题2）‎ P Q C R O E D B A ‎1‎ ‎3‎ ‎2‎ G ②方法一：如图2，当点P在BC上运动，‎ 使△PQR与△COB相似时，‎ ‎∵∠2是△OBP的外角，∴∠2＞∠3，‎ ‎∴∠2不与∠3对应，∴∠2与∠1对应，‎ 即∠2＝∠1，∴OP=OC=3（5分）， ‎ ‎ 过O作OG⊥BC于G，则G为PC的中点，△OGC∽△BOC，（6分）‎ ‎∴CG:CO＝CO:BC，即：CG:3＝3:5，∴CG=，（7分）‎ ‎∴PB＝BC－PC＝BC－2CG＝5－2×＝.（8分）‎ 方法二：如图3，当点P在BC上运动，‎ 使△PQR与△COB相似时，‎ ‎（第24题3）‎ P Q C R O E D B A ‎1‎ ‎3‎ ‎2‎ F ‎∵∠2是△OBP的外角，∴∠2＞∠3，‎ ‎∴∠2不与∠3对应，∴∠2与∠1对应，（5分）‎ ‎∴QR:BO＝PR:OC，即：:4＝PR:3，‎ ‎∴PR＝，（6分）‎ 过E作EF⊥BD于F，设PB＝x，则RF=QE=PB=x，‎ DF＝==，（7分）‎ ‎∴BD＝PB＋PR＋RF＋DF＝x＋＋x＋＝10，x＝.（8分）‎ 方法三: 如图4，若点P在BC上运动，使点R与C重合，‎ ‎(R)‎ P C O D Q E B A ‎（第24题4）‎ 由菱形的对称性知，O为PQ的中点，‎ ‎∴CO是Rt△PCQ斜边上的中线，‎ ‎∴CO=PO，（5分）∴∠OPC＝∠OCP，‎ 此时，Rt△PQR∽Rt△CBO，（6分）‎ ‎∴PR:CO＝PQ:BC，即PR:3＝6:5，‎ ‎∴PR＝（7分），∴PB＝BC-PR＝5－＝.（8分）‎ ‎25.解(1)∵抛物线顶点(h，m)在直线y＝kx上，∴m＝kh；(1分)‎ ‎(2) 方法一：解方程组，‎ 将(2)代入(1)得到： (x－h)2＋kh＝kx，‎ 整理得：(x－h)[(x－h)－k]＝0，‎ 解得：x1＝h， x2＝k＋h 代入到方程(2) y1＝h y2＝k2＋hk 所以点E坐标是(k＋h，k2＋hk) (1分)‎ 当x＝0时，y＝(x－h)2＋m＝h2＋kh，‎ ‎∴点F坐标是(0，h2＋kh)‎ 当EF和x轴平行时，点E，F的纵坐标相等，‎ 即k2＋kh＝h2＋kh 解得：h＝k(h＝－k舍去，否则E，F，O重合)(2分)‎ 此时点E(2k，2k2)，F(0，2k2)，C(k,2k2)， A(k，k2)‎ ‎∴AC∶OF＝k2∶2 k2 =1∶2(3分)‎ 方法二：当x＝0时，y＝(x－h)2＋m＝h2＋kh，即F (0，h2＋kh)‎ 当EF和x轴平行时，点E，F的纵坐标相等 即点E的纵坐标为h2＋kh 当y＝h2＋kh时，代入y＝(x－h)2＋kh，‎ 解得x＝2h(0舍去，否则E，F，O重合)，‎ 即点E坐标为(2h，h2＋kh)，(1分)‎ 将此点横纵坐标代入y＝kx得到h＝k(h＝0舍去，否则点E，F，O重合) (2分)‎ 此时点E(2k，2k2)，F(0，2k2)，C(k,2k2)，A(k，k2)‎ ‎∴AC∶OF＝k2∶2 k2 =1∶2(3分)‎ 方法三： ∵EF与x轴平行，‎ 根据抛物线对称性得到FC＝EC(1分)‎ ‎∵AC∥FO，∴∠ECA＝EFO，∠FOE＝∠CAE ‎∴△OFE∽△ACE，(2分)‎ ‎∴AC∶OF＝EC∶EF＝1∶2(3分)‎ ‎(3)当点F的位置处于最低时，其纵坐标h2＋kh最小，(1分)‎ ‎∵h2＋kh＝－，‎ 当h＝，点F的位置最低，此时F(0，－)(2分)‎ 解方程组得E(，)，A(－，－) (3分)‎ 方法一：设直线EF的解析式为y＝px＋q，‎ 将点E(，)，F(0，－)的横纵坐标分别代入得(4分)‎ 解得：p＝，q＝－，‎ ‎∴直线EF的解析式为y＝x－ (5分)‎ 当x＝－时，y＝－k2，即点C的坐标为(－，－k2)，‎ ‎∵点A(－，－)，所以AC＝，而OF=，‎ ‎∴AC＝2OF，即AC∶OF＝2。(6分)‎ 方法二：∵E(，)，A(－，－)‎ ‎∴点A，E关于点O对称，∴AO＝OE，(4分)‎ ‎∵AC∥FO，∴∠ECA＝EFO，∠FOE＝∠CAE ‎∴△OFE∽△ACE，(5分)‎ ‎∴AC∶OF＝EC∶EF＝1∶2(6分)‎