2013广安市中考数学试题解答 8页

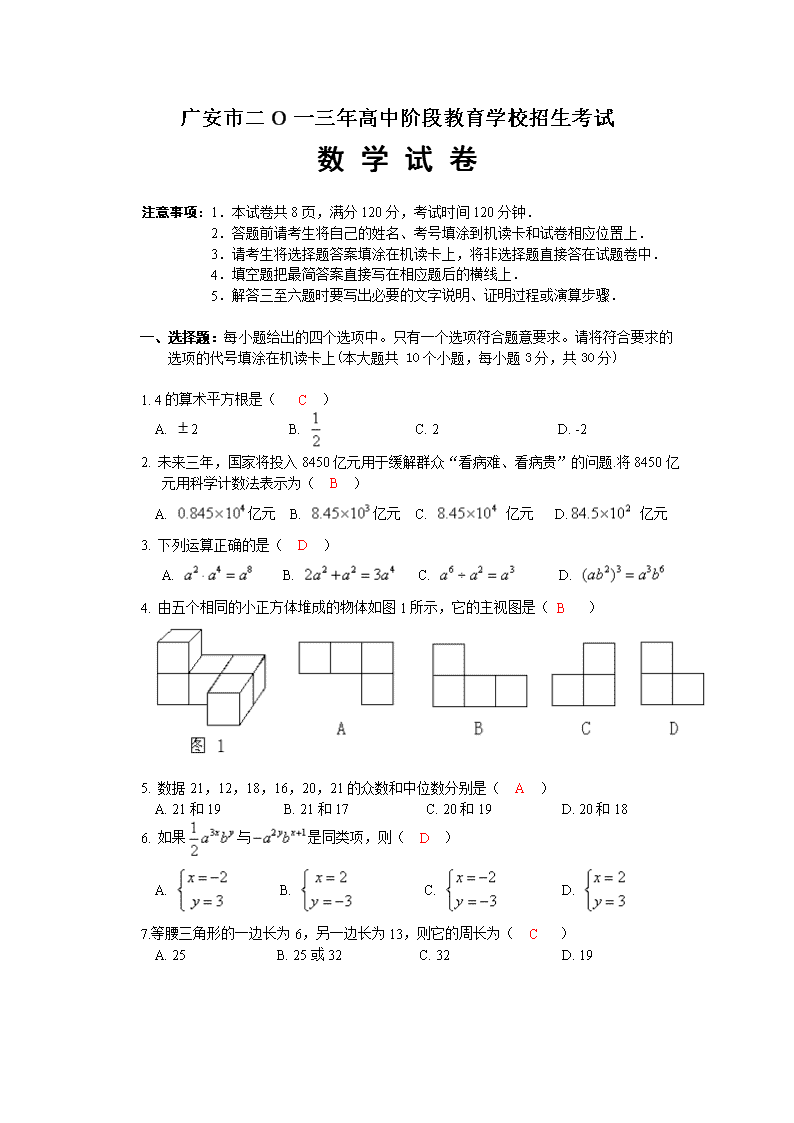
广安市二O一三年高中阶段教育学校招生考试 数 学 试 卷 注意事项：1．本试卷共8页，满分120分，考试时间120分钟．‎ ‎2．答题前请考生将自己的姓名、考号填涂到机读卡和试卷相应位置上．‎ ‎3．请考生将选择题答案填涂在机读卡上，将非选择题直接答在试题卷中．‎ ‎4．填空题把最简答案直接写在相应题后的横线上．‎ ‎5．解答三至六题时要写出必要的文字说明、证明过程或演算步骤．‎ 一、选择题：每小题给出的四个选项中。只有一个选项符合题意要求。请将符合要求的选项的代号填涂在机读卡上(本大题共 10个小题，每小题3分，共30分)‎ ‎ 1. 4的算术平方根是（ C ）‎ ‎ A. 2 B. C. 2 D. -2‎ ‎ 2. 未来三年，国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题.将8450亿元用科学计数法表示为（ B ）‎ ‎ A. 亿元 B. 亿元 C. 亿元 D. 亿元 ‎ 3. 下列运算正确的是（ D ）‎ ‎ A. B. C. D. ‎ ‎ 4. 由五个相同的小正方体堆成的物体如图1所示，它的主视图是（ B ）‎ ‎ ‎ ‎ 5. 数据21，12，18，16，20，21的众数和中位数分别是（ A ）‎ ‎ A. 21和19 B. 21和‎17 C. 20和19 D. 20和18‎ ‎ 6. 如果与是同类项，则（ D ）‎ ‎ A. B. C. D. ‎ ‎ 7.等腰三角形的一边长为6，另一边长为13，则它的周长为（ C ）‎ ‎ A. 25 B. 25或‎32 C. 32 D. 19‎ ‎ ‎ ‎ 8.下列命题中，正确的是（ D ）‎ A. 函数的自变量x的取值范围是x＞3‎ ‎ B. 菱形是中心对称图形，但不是轴对称图形 C. 一组对边平行，另一组对边相等的四边形是平行四边形 D. 三角形的外心到三角形的三个顶点的距离相等 ‎ 9. 如图2，已知半径OD与弦AB互相垂直，垂足为点C，若AB=‎8cm， CD=‎3cm，则圆O的半径为（ A ）‎ ‎ A. cm B. ‎‎5cm ‎ C. ‎4cm D. cm ‎ 10. 已知二次函数的图像如图3所示，对称轴是直 线x=1. 下列结论：①abc＞0，②2a+b=0，③，‎ ‎④‎4a+2b+c＞0，其中正确的是（ C ）‎ A. ①③ B. 只有②‎ C. ②④ D. ③④‎ ‎ ‎ 二、填空题：请把最简答案直接填写在置后的横线上(本大题共6个小题，每小题3分，共18分)‎ ‎ 11. 方程的根是_x=1或x=2 .‎ ‎ 12. 将点A（-1，2）沿x轴向右平移3个单位长度，再沿y轴向下平移4个单位长度后得到点的坐标为 ( 2 , -2 ) . ‎ ‎ 13. 如图4，若1=40°，2=40°，3=116°30′，‎ ‎ 则4=_163°30′_.‎ ‎ 14. 解方程：，则方程的解是 ‎__x = - __. ‎ ‎15. 如图5，如果从半径为‎5cm的圆形纸片上剪去 ‎ 圆周的一个扇形，将留下的扇形围成一个圆锥 ‎（接线处不重叠），那么这个圆锥的高是_3_cm. ‎ ‎ 16. 已知直线（n为正整数）‎ ‎ 与两坐标轴围成的三角形的面积为，则= .‎ 三、解答题（本大题共4个小题，第17小题5分，第18、19、20小题各6分．共23分）‎ ‎ 17. 计算：‎ ‎ 解：原式= 2 + -1+2-2- ‎ =1‎ ‎ 18. 先化简，再求值：，其中x=4‎ ‎ 解：原式= ×= ,‎ ‎ 将x = 4 代入，‎ ‎ 原式= = - ‎ 19. 如图6，在平行四边形ABCD中，AE∥CF，‎ ‎ 求证：△ABE△CDF ‎ 证明：∵AE//CF，∴∠CFD=∠EAD， ‎ ‎∵四边形ABCD为平行四边形，‎ ‎ ∴AD//BC，∠EAD=∠AEB，∠CFD=∠AEB， ‎ ‎ ∠B=∠D，AB=CD，‎ ‎∴△ABE≌△CDF.‎ ‎ 20. 已知反比例函数和一次函数.‎ ‎ (1) 若一次函数与反比例函数的图像交于点P（2，m），求m和k的值.‎ ‎ (2) 当k满足什么条件时，两函数的图像没有交点？‎ ‎ 解：(1)点P（2，m）是反比例函数y = 和一次函数y=x-6的图像的交点，‎ ‎ m = 2-6 = -4, -4 = , k = - 8 ;‎ ‎ (2) = x-6 , x2-6x-k=0 ,当此一元二次方程根的判别式小于0时，‎ 两函数图像无交点，‎ ‎△=（-6）2 - 4（-k）= 36 + 4k < 0 , k < -9 .‎ ‎ 当k < - 9时，两函数的图像没有交点。‎ 四、实践应用（本大题共4个小题，其中第21小题6分，第22、23、24每小题8分，共30分）‎ ‎ 21. ‎6月5日是“世界环境日”，广安市某校举行了“洁美家园”的演讲比赛，赛后整理参赛同学的成绩，将学生的成绩分成A、B、C、D四个等级，并制成如下的条形统计图和扇形图（如图7、8）‎ ‎ (1) 补全条形统计图.‎ ‎ (2) 学校决定从本次比赛中获得A等和B等的学生中各选出一名去参加市中学生环保演讲比赛. 已知A等中有男生2名，B等中有女生3名. 请你用“列表法”或“树形图法”的方法求出所选两位同学恰好是一名男生和一名女生的概率.‎ ‎ 解：A等中有3人，2男1女，B等中有5人，2男3女， ‎ B 等 组 合 A 等 男3‎ 男4‎ 女2‎ 女3‎ 女4‎ 男1‎ 男1男3‎ 男1男4‎ 男1女2‎ 男1女3‎ 男1女4‎ 男2‎ 男2男3‎ 男2男4‎ 男2女2‎ 男2女3‎ 男2女4‎ 女1‎ 女1男3‎ 女1男4‎ 女1女2‎ 女1女3‎ 女1女4‎ ‎ 由上表可知，共有15种组合，其中一男一女的组合有8种，‎ ‎ 所以所选两位同学恰好是一名男生和一名女生的概率是 .‎ 空调 彩电 进价（元／台）‎ ‎5400‎ ‎3500‎ 售价（元／台）‎ ‎6100‎ ‎3900‎ ‎22. 某商场筹集资金12.8万元，一次性购进空调、彩电共30台. 根据市场需要，这些空调、彩电可以全部销售，全部销售后利润不少于1.5万元，其中空调、彩电的进价和售价见右表.‎ ‎ 设商场计划购进空调x台，空调和彩电全部销售后商场获得的利润为y元.‎ ‎ （1） 试写出y与x的函数关系式；‎ ‎ （2） 商场有哪几种进货方案可供选择？‎ ‎ （3） 选择哪种进货方案，商场获利最大？最大利润是多少元？‎ ‎ 解：（1）商场计划购进空调x台，则购进彩电30- x台，‎ ‎ y = (6100-5400)x+(3900-3500)(30-x), 整理得：‎ ‎ y = 300x + 12000 ‎ ‎ (2) 5400x + 3500(30-x)≤ 128000‎ ‎ 解得10≤x≤12 ,‎ y = 300x + 12000≥15000 , ‎ ‎ 空调台数只能是整数，所以x=10,11或12;‎ ‎ 所以商场共有3种进货方案可供选择：‎ 方案一：购进空调10台，彩电20台，‎ 方案二：购进空调11台，彩电19台，‎ 方案三：购进空调12台，彩电18台；‎ ‎ （3）y = 300x + 12000是增函数，y随着x的增大而增大，所以商场选择方案三（购进空调12台，彩电18台）能获得最大利润，‎ ‎ 此时,最大利润y =300×12 + 12000 = 15600元。‎ ‎ 23. 如图9，广安市防洪指挥部发现渠江边一处长‎400米，高‎8米，背水坡的坡角为45°‎ 的防洪大堤（横断面为梯形ABCD）急需加固. 经调查论证，防洪指挥部专家制定的加固方案是：背水坡面用土石进行加固，并使上底加宽‎2米，加固后，背水坡EF的坡比为I =1∶2.‎ ‎ （1）求加固后坝底增加的宽度AF的长；‎ ‎ （2）求完成这项工程需要的土石为多少 立方米？‎ ‎ 解：（1）分别过点D、E作DG⊥AB 、EH⊥AB于点G和H，EH = DG = 8（米），‎ ‎ DE=GH=2（米），AH = cot45°×EH = 8（米），= 1:2 ，‎ FG = 2DG=2×8=16（米）， AF = FG + GH – AH = 16+2-8 =10（米）；‎ ‎(2）S梯形AFDE = (AF + DE)•DG =×(10+2) ×8 = 48(米2)，‎ ‎ V梯柱= S梯形AFDE×400 = 48×400=19200（米3）‎ 答：加固后坝底增加的宽度AF的长为‎10米，完成这项工程需要土石‎19200米3。‎ ‎ 24. 雅安芦山发生7.0级地震后，某校师生准备了一些等腰直角三角形纸片，从每张纸片中剪出一个半圆制作玩具，寄给灾区的小朋友. 已知如图10，是腰长为4的等腰直角三角形ABC，要求剪出的半圆的直径在△ABC的边上，且半圆的弧与△ABC的其他两边相切，请作出所有不同方案的示意图，并求出相应半圆的半径（结果保留根号）.‎ ‎ 解：不同方案作图分别如 图10.1 、 图10.2 和 图10.3 ；‎ ‎ ① 如图10.1，直径在AC上，点O为圆心，AB与圆相切，OD⊥AB，OD是圆的半径，‎ ‎ △ACB是等腰直角三角形，AC=BC=4, BA = =4,AB⊥BC，AC是直径所在直线，BC是圆的切线，BC必过半径的的外端，OC是圆的半径，OD=OC=r,‎ ‎∠AD0=∠ACB，∠A=∠A，△ACB∽△AD0， = , = , r=4-r,‎ r= 4-4 ；‎ ‎② 如图10.2，同理可得 r=4-4 ；‎ ‎③ 如图10.3，AC、BC分别与圆相切于点E、F，OE=OF=r， OE⊥AC，OF⊥BC，‎ AC⊥BC，∠OEC=∠ECF=∠CFO=∠FOE=90°, 四边形OECF是正方形，OF//AC，‎ ‎△ACB∽△OFB，△OFB是等腰直角三角形，OF=FB，OE=FC=FB，点F是BC的中点，BC=4， CF = BC = 2，r=OE=CF=2.‎ 五、推理与论证（9分）‎ ‎ 25. 如图11，在△ABC中，AB=AC，以AB为直径作半圆⊙O，交BC于点D，连接AD，过点D作DE⊥AC，垂足为点E，交AB的延长线于点F.‎ ‎ （1）求证：EF是⊙O的切线.‎ ‎ （2）如果⊙O的半径为5，，求BF的长.‎ ‎ 解：（1）证明：连结OD，‎ ‎∵AB是⊙O的直径，D为圆上一点， ∴∠ADB=90°，AD⊥BC，‎ ‎ ∵在△ABC中，AB=AC， ∴ △ABC为等腰三角形，AD是其底边上的高，‎ 也是顶角∠CAB的平分线， ∠CAD=∠OAD， ‎ ‎ ∵ OD=OA， ∴∠OAD=∠ODA， ∠CAD=∠ODA， OD//AC， ‎ ‎∵DE⊥AC， DE⊥OD，‎ ‎∴DE是⊙O的切线（过直径的外端且垂直于直径的直线是圆的切线）。‎ ‎（2）∠AED=∠ADB= 90°，∠EAD=∠DAB，△EAD∽△DAB，OD = r = 5，AB=2r=10，‎ sin∠ADE = = = , AD = AB = 8 , AE = AD = , ‎ DE = = = ,‎ BD = = = 6 ,‎ OD//AE, = = 5×= , = , = ,‎ DF= , ‎ ‎∠OBD=∠ODB, ∠ODB +∠BDF =∠OBD +∠DAF = 90°,∠BDF =∠DAF, ∠F =∠F,‎ ‎△BDF∽△DAF, = , BF = = = .‎ 六、拓展探究（10分）‎ ‎ 26. 如图12，在平面直角坐标系xoy中，抛物线经过A、B、C、三点，已知点A（-3，0），B（0，3），C（1，0）.‎ ‎ （1）求此抛物线的解析式.‎ ‎ （2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为点F，交直线AB于点E，作PD⊥AB于点D.‎ ‎ ①动点P在什么位置时，△PDE的周长最大，求出此时P点的坐标；‎ ‎ ②连接PA，以AP为边作图示一侧的正方形APMN，随着点P的运动，正方形的大小、位置也随之改变. 当顶点M或N恰好落在抛物线对称轴上时，求出对应的P点的坐标. （结果保留根号）‎ ‎ 解：（1） 抛物线y = ax2+bx+c的图像过点A（-3，0）、‎ ‎ C（1，0）、B（0，3），c =3, ‎ ‎ 一元二次方程ax2+bx+3=0的两个根为 -3、‎ ‎1 ，根据韦达定理可知：‎ ‎(-3)×1= , a = -1 , ‎ ‎-3 + 1 = - = b , b = -2 ,‎ 所以抛物线的解析式为 y = - x2 - 2x + 3 ；‎ ‎（2）如图12.1， OA =OB=3，OA⊥OB，‎ ‎△AOB是等腰直角三角形，‎ ‎ PF⊥OA ，PF//OB，∠PED=∠AEF =∠ABO，PD⊥AB ，∠PDE=∠AOB=90°，‎ ‎ △EDP∽△AOB，△PDE是等腰直角三角形，要使等腰直角△PDE的周长最大，则其斜边PE必须有最大值，‎ 直线AB的解析式为 y = x + 3 ,点E在直线y = x + 3上，‎ 点P在抛物线y = - x2 - 2x + 3上，‎ 令点P的坐标为（x, - x2 - 2x + 3），则点E的坐标为（x, x+3）,点P在直线AB的上方，且不与点A、B重合，所以 -3 < x < 0 ，‎ PE= - x2 - 2x + 3 -（x + 3）= - x 2 - 3x = -（x + ）2 + , ‎ 当x = - 时（符合-3 < x < 0），PE有最大值 ，‎ 此时， - x2 - 2x + 3 = -（）2 - 2×（- ）+3 = ,‎ 所以，△PDE的周长最大时，点P的坐标为（- ，）；‎ ‎ （3）抛物线的对称轴为x = = -1 , ‎ 令点P的坐标为（x, - x2 - 2x + 3），-3 < x < 0‎ ① 如图12.1，当点M在直线x = -1上时，显然点P在抛物线对称轴的左侧，‎ 过点P作 直线x = -1的垂线，垂足为Q，PQ//x轴，‎ ‎∠PQM=∠PFA= 90°= ∠FPQ， 四边形APMN为正方形，PA=PM，‎ ‎∠QPM+∠MPF=∠FPA+∠MPF=90°，∠QPM =∠FPA，△QPM≌△FPA，PQ=PF，‎ ‎-1- x = - x2 - 2x + 3 ，x = >0 (不合题意，舍去) 或 x = ，- x2 - 2x + 3 = ，‎ 此时有点P（，）‎ ‎② 如图12.2，当点N在直线x = -1上时，‎ 抛物线对称轴与x轴交于点Q，‎ ‎∠PAF +∠FPA=90°，∠PAF+∠QAN=90°， ‎ ‎∠FPA=∠QAN，∠PFA=∠AQN=90°，PA=AN ， ‎ △ APF≌△NAQ，PF = AQ， ‎ ‎- x2 - 2x + 3 = -1-（-3）=2， ‎ x= -1>0(不合题意，舍去)或 ‎ x= - -1， - x2 - 2x + 3 = 2， ‎ 此时有点P（- -1，2 ）； ‎ 综上所述，当顶点M恰好落在抛物线对称 ‎ 轴上时，点P的坐标为（，），当顶点N恰好落在抛物线对称轴上时，点P的 ‎ 坐标为（- -1，2 ）。 ‎