中考数学专题练习卷 二元一次方程组解析 17页

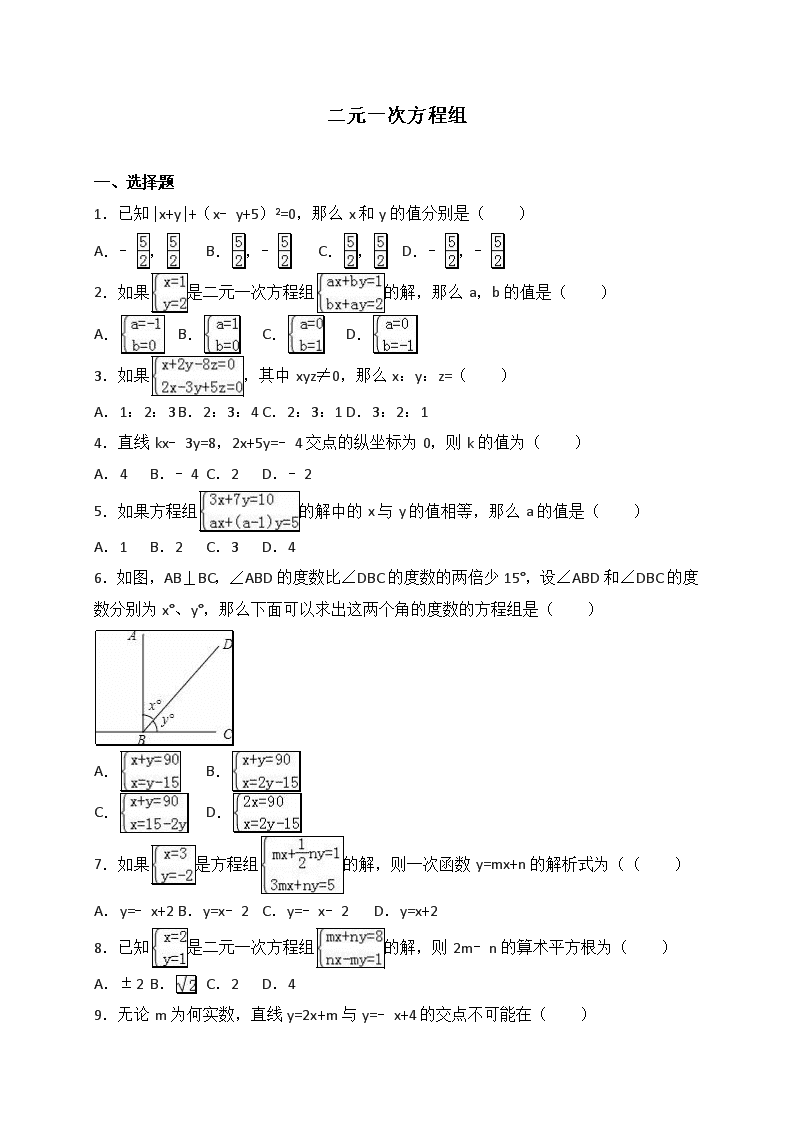
二元一次方程组 ‎　‎ 一、选择题 ‎1．已知|x+y|+（x﹣y+5）2=0，那么x和y的值分别是（　　）‎ A．﹣， B．，﹣ C．， D．﹣，﹣‎ ‎2．如果是二元一次方程组的解，那么a，b的值是（　　）‎ A． B． C． D．‎ ‎3．如果，其中xyz≠0，那么x：y：z=（　　）‎ A．1：2：3 B．2：3：‎4 ‎C．2：3：1 D．3：2：1‎ ‎4．直线kx﹣3y=8，2x+5y=﹣4交点的纵坐标为0，则k的值为（　　）‎ A．4 B．﹣‎4 ‎C．2 D．﹣2‎ ‎5．如果方程组的解中的x与y的值相等，那么a的值是（　　）‎ A．1 B．‎2 ‎C．3 D．4‎ ‎6．如图，AB⊥BC，∠ABD的度数比∠DBC的度数的两倍少15°，设∠ABD和∠DBC的度数分别为x°、y°，那么下面可以求出这两个角的度数的方程组是（　　）‎ A． B．‎ C． D．‎ ‎7．如果是方程组的解，则一次函数y=mx+n的解析式为（（　　）‎ A．y=﹣x+2 B．y=x﹣‎2 ‎C．y=﹣x﹣2 D．y=x+2‎ ‎8．已知是二元一次方程组的解，则‎2m﹣n的算术平方根为（　　）‎ A．±2 B． C．2 D．4‎ ‎9．无论m为何实数，直线y=2x+m与y=﹣x+4的交点不可能在（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎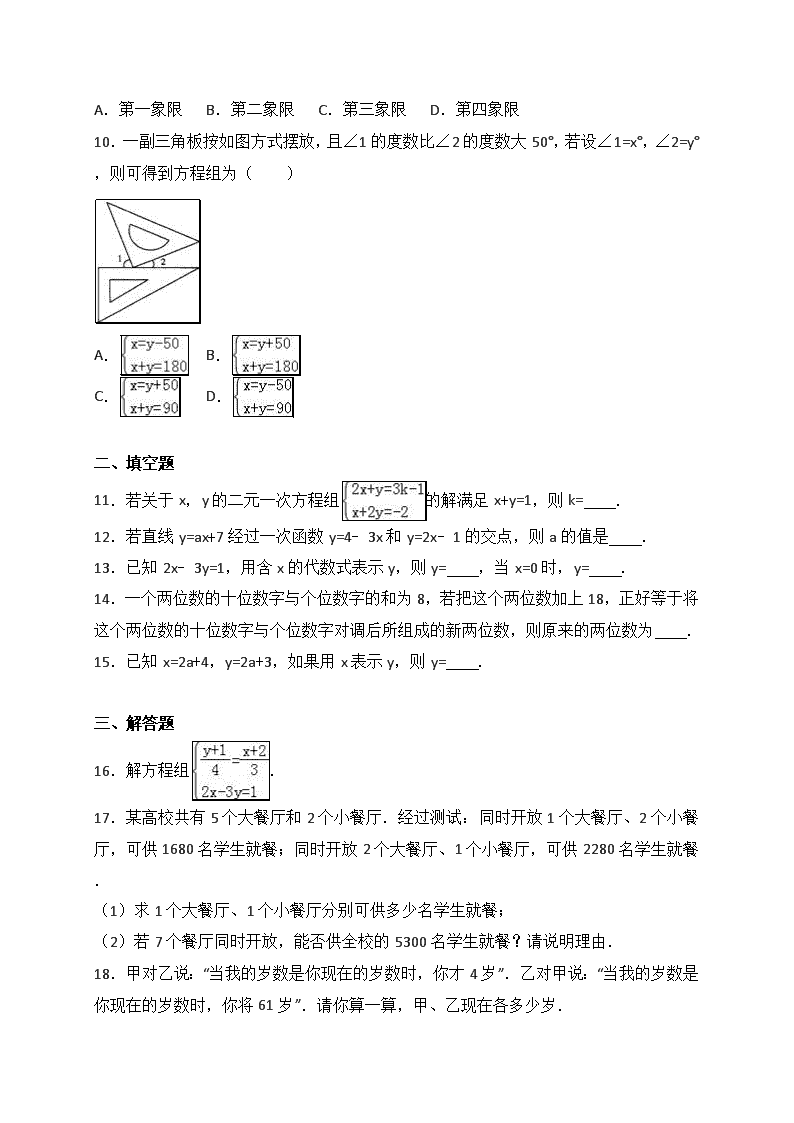10．一副三角板按如图方式摆放，且∠1的度数比∠2的度数大50°，若设∠1=x°，∠2=y°，则可得到方程组为（　　）‎ A． B．‎ C． D．‎ ‎　‎ 二、填空题 ‎11．若关于x，y的二元一次方程组的解满足x+y=1，则k=　　．‎ ‎12．若直线y=ax+7经过一次函数y=4﹣3x和y=2x﹣1的交点，则a的值是　　．‎ ‎13．已知2x﹣3y=1，用含x的代数式表示y，则y=　　，当x=0时，y=　　．‎ ‎14．一个两位数的十位数字与个位数字的和为8，若把这个两位数加上18，正好等于将这个两位数的十位数字与个位数字对调后所组成的新两位数，则原来的两位数为　　．‎ ‎15．已知x=‎2a+4，y=‎2a+3，如果用x表示y，则y=　　．‎ ‎　‎ 三、解答题 ‎16．解方程组．‎ ‎17．某高校共有5个大餐厅和2个小餐厅．经过测试：同时开放1个大餐厅、2个小餐厅，可供1680名学生就餐；同时开放2个大餐厅、1个小餐厅，可供2280名学生就餐．‎ ‎（1）求1个大餐厅、1个小餐厅分别可供多少名学生就餐；‎ ‎（2）若7个餐厅同时开放，能否供全校的5300名学生就餐？请说明理由．‎ ‎18．甲对乙说：“当我的岁数是你现在的岁数时，你才4岁”．乙对甲说：“当我的岁数是你现在的岁数时，你将61岁”．请你算一算，甲、乙现在各多少岁．‎ ‎19．有甲乙两种铜和银的合金，甲种合金含银25%，乙种合金含银37.5%，现在要熔制含银30%的合金100千克，甲、乙两种合金各应取多少？‎ ‎20．甲乙两地相距160千米，一辆汽车和一辆拖拉机从两地同时出发相向而行，1小时20分后相遇．相遇后，拖拉机继续前进，汽车在相遇处停留1小时后原速返回，在汽车再次出发半小时后追上了拖拉机，这时汽车、拖拉机从开始到现在各自行驶了多少千米？‎ ‎21．如图，某化工厂与A，B两地有公路和铁路相连，这家工厂从A地购买一批每吨1 000元的原料运回工厂，制成每吨8 000元的产品运到B地．已知公路运价为1.5元/（吨•千米），铁路运价为1.2元/（吨•千米），这两次运输共支出公路运费15 000元，铁路运费97 200元，请计算这批产品的销售款比原料费和运输费的和多多少元？‎ ‎（1）根据题意，甲、乙两名同学分别列出尚不完整的方程组如下：‎ 甲：‎ 乙：‎ 根据甲，乙两名同学所列方程组，请你分别指出未知数x，y表示的意义，然后在等式右边的方框内补全甲、乙两名同学所列方程组．‎ 甲：x表示　　，y表示　　‎ 乙：x表示　　，y表示　　‎ ‎（2）甲同学根据他所列方程组解得x=300，请你帮他解出y的值，并解决该实际问题．‎ ‎　‎ 二元一次方程组 参考答案与试题解析 ‎　‎ 一、选择题 ‎1．已知|x+y|+（x﹣y+5）2=0，那么x和y的值分别是（　　）‎ A．﹣， B．，﹣ C．， D．﹣，﹣‎ ‎【考点】解二元一次方程组；非负数的性质：绝对值；非负数的性质：偶次方．‎ ‎【分析】根据绝对值和偶次方得出关于x、y的方程组，求出方程组的解即可．‎ ‎【解答】解：∵|x+y|+（x﹣y+5）2=0，‎ ‎∴x+y=0，x﹣y+5=0，‎ 即，‎ ‎①+②得：2x=﹣5，‎ 解得：x=﹣，‎ 把x=﹣代入①得：y=，‎ 即方程组的解为，‎ 故选A．‎ ‎【点评】本题考查了解二元一次方程组和解一元一次方程的应用，关键是能得出关于x、y的方程组．‎ ‎　‎ ‎2．如果是二元一次方程组的解，那么a，b的值是（　　）‎ A． B． C． D．‎ ‎【考点】二元一次方程组的解．‎ ‎【专题】计算题．‎ ‎【分析】将x=1，y=2代入方程组得到关于a与b的方程组，即可求出a与b的值．‎ ‎【解答】解：将x=1，y=2代入方程组得：，‎ ‎①×2﹣②得：3b=3，‎ 即b=0，‎ 将b=1代入①得：a=1，‎ 则．‎ 故选B．‎ ‎【点评】此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程成立的未知数的值．‎ ‎　‎ ‎3．如果，其中xyz≠0，那么x：y：z=（　　）‎ A．1：2：3 B．2：3：‎4 ‎C．2：3：1 D．3：2：1‎ ‎【考点】解三元一次方程组．‎ ‎【分析】理解清楚题意，运用三元一次方程组的知识，把x，y用z表示出来，代入代数式求值．‎ ‎【解答】解：已知，‎ ‎①×2﹣②得，7y﹣21z=0，‎ ‎∴y=3z，‎ 代入①得，x=8z﹣6z=2z，‎ ‎∴x：y：z=2z：3z：z=2：3：1．‎ 故选C．‎ ‎【点评】本题的实质是解三元一次方程组，用加减法或代入法来解答．‎ ‎　‎ ‎4．直线kx﹣3y=8，2x+5y=﹣4交点的纵坐标为0，则k的值为（　　）‎ A．4 B．﹣‎4 ‎C．2 D．﹣2‎ ‎【考点】两条直线相交或平行问题．‎ ‎【专题】计算题．‎ ‎【分析】本题可先根据函数2x+5y=﹣4求出交点的坐标，然后将交点坐标代入直线kx﹣3y=8中，即可求出k的值．‎ ‎【解答】解：在直线2x+5y=﹣4中，‎ 当y=0时，2x=﹣4，‎ ‎∴x=﹣2．‎ ‎∴这两条直线的交点坐标为（﹣2，0）．‎ 将（﹣2，0）代入kx﹣3y=8中，得：﹣2k=8，‎ ‎∴k=﹣4．‎ 故选B．‎ ‎【点评】解答此题应根据两直线相交时，函数图象的交点应同时满足两个函数的解析式．‎ ‎　‎ ‎5．如果方程组的解中的x与y的值相等，那么a的值是（　　）‎ A．1 B．‎2 ‎C．3 D．4‎ ‎【考点】解三元一次方程组．‎ ‎【分析】理解清楚题意，运用三元一次方程组的知识，解出a的数值 ‎【解答】解：根据题意得，‎ 把（3）代入（1）得：3y+7y=10，‎ 解得：y=1，x=1，‎ 代入（2）得：a+（a﹣1）=5，‎ 解得：a=3．‎ 故选C．‎ ‎【点评】本题的实质是解三元一次方程组，用加减法或代入法来解答．‎ ‎　‎ ‎6．如图，AB⊥BC，∠ABD的度数比∠DBC的度数的两倍少15°，设∠ABD和∠DBC的度数分别为x°、y°，那么下面可以求出这两个角的度数的方程组是（　　）‎ A． B．‎ C． D．‎ ‎【考点】由实际问题抽象出二元一次方程组．‎ ‎【专题】计算题．‎ ‎【分析】根据两角互余和题目所给的关系，列出方程组．‎ ‎【解答】解：设∠ABD和∠DBC的度数分别为x°、y°，‎ 由题意得，．‎ 故选B．‎ ‎【点评】本题考查了由实际问题抽象出二元一次方程组，解答本题的关键是根据题意找出合适的等量关系列方程组．‎ ‎　‎ ‎7．如果是方程组的解，则一次函数y=mx+n的解析式为（（　　）‎ A．y=﹣x+2 B．y=x﹣‎2 ‎C．y=﹣x﹣2 D．y=x+2‎ ‎【考点】一次函数与二元一次方程（组）．‎ ‎【分析】把方程组的解代入方程组得到关于m、n的方程组，然后求出m、n的值，再代入函数解析式即可得解．‎ ‎【解答】解：根据题意，将代入方程组，‎ 得，‎ 即，‎ ‎①×2得，‎6m﹣2n=2…③，‎ ‎②﹣③得，‎3m=3，‎ ‎∴m=1，‎ 把m=1代入①，得，3﹣n=1，‎ ‎∴n=2，‎ ‎∴一次函数解析式为y=x+2．‎ 故选D．‎ ‎【点评】本题考查了一次函数与二元一次方程组，根据方程组的解的定义得到关于m、n的方程组并求出m、n的值是解题的关键．‎ ‎　‎ ‎8．已知是二元一次方程组的解，则‎2m﹣n的算术平方根为（　　）‎ A．±2 B． C．2 D．4‎ ‎【考点】二元一次方程组的解；算术平方根．‎ ‎【分析】由是二元一次方程组的解，根据二元一次方程根的定义，可得，即可求得m与n的值，继而求得‎2m﹣n的算术平方根．‎ ‎【解答】解：∵是二元一次方程组的解，‎ ‎∴，‎ 解得：，‎ ‎∴‎2m﹣n=4，‎ ‎∴‎2m﹣n的算术平方根为2．‎ 故选C．‎ ‎【点评】此题考查了二元一次方程组的解、二元一次方程组的解法以及算术平方根的定义．此题难度不大，注意理解方程组的解的定义．‎ ‎　‎ ‎9．无论m为何实数，直线y=2x+m与y=﹣x+4的交点不可能在（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎【考点】两条直线相交或平行问题．‎ ‎【专题】计算题．‎ ‎【分析】直线y=﹣x+4经过第一，二，四象限，一定不经过第三象限，因而直线y=2x+m与直线y=﹣x+4的交点不可能在第三象限．‎ ‎【解答】解：由于直线y=﹣x+4的图象不经过第三象限．‎ 因此无论m取何值，直线y=2x+m与直线y=﹣x+3的交点不可能在第三象限．‎ 故选C．‎ ‎【点评】本题考查了两条直线相交的问题，需注意应找到完整的函数，进而找到它不经过的象限，那么交点就一定不在那个象限．‎ ‎　‎ ‎10．一副三角板按如图方式摆放，且∠1的度数比∠2的度数大50°，若设∠1=x°，∠2=y°，则可得到方程组为（　　）‎ A． B．‎ C． D．‎ ‎【考点】由实际问题抽象出二元一次方程组；余角和补角．‎ ‎【分析】此题中的等量关系有：‎ ‎①三角板中最大的角是90°，从图中可看出∠1+∠2+90°=180°；‎ ‎②∠1比∠2的度数大50°，则∠1=∠2+50°．‎ ‎【解答】解：根据平角和直角定义，得方程x+y=90；‎ 根据∠1比∠2的度数大50°，得方程x=y+50．‎ 可列方程组为，‎ 故选：C．‎ ‎【点评】此题考查了学生对二元一次方程组的灵活运用，学生应该重视培养对应用题的理解能力，准确地列出二元一次方程组．‎ ‎　‎ 二、填空题 ‎11．若关于x，y的二元一次方程组的解满足x+y=1，则k=　2　．‎ ‎【考点】二元一次方程组的解．‎ ‎【分析】直接将方程组中两方程相加得出3x+3y=3k﹣3，进而求出k的值．‎ ‎【解答】解：∵关于x，y的二元一次方程组的解满足x+y=1，‎ ‎∴3x+3y=3k﹣3，‎ ‎∴x+y=k﹣1=1，‎ 解得：k=2．‎ 故答案为：2．‎ ‎【点评】此题主要考查了二元一次方程组的解，将两方程相加得出k的值是解题关键．‎ ‎　‎ ‎12．若直线y=ax+7经过一次函数y=4﹣3x和y=2x﹣1的交点，则a的值是　﹣6　．‎ ‎【考点】两条直线相交或平行问题；待定系数法求一次函数解析式．‎ ‎【分析】首先联立解方程组，求得直线y=4﹣3x和y=2x﹣1的交点，再进一步代入y=ax+7中求解．‎ ‎【解答】解：根据题意，得 ‎4﹣3x=2x﹣1，‎ 解得x=1，‎ ‎∴y=1．‎ 把（1，1）代入y=ax+7，‎ 得a+7=1，‎ 解得a=﹣6．‎ 故答案为：﹣6．‎ ‎【点评】此题考查了两条直线的交点的求法，即联立解方程组求解即可．‎ ‎　‎ ‎13．已知2x﹣3y=1，用含x的代数式表示y，则y=　　，当x=0时，y=　﹣　．‎ ‎【考点】解二元一次方程．‎ ‎【专题】计算题．‎ ‎【分析】将x看做已知数，求出y即可；将x=0代入计算即可求出y的值．‎ ‎【解答】解：2x﹣3y=1，‎ 变形得：y=，‎ 将x=0代入，得：y=﹣．‎ 故答案为：；﹣‎ ‎【点评】此题考查了解二元一次方程，解题的关键是将x看做已知数，y看做未知数．‎ ‎　‎ ‎14．一个两位数的十位数字与个位数字的和为8，若把这个两位数加上18，正好等于将这个两位数的十位数字与个位数字对调后所组成的新两位数，则原来的两位数为　35　．‎ ‎【考点】二元一次方程组的应用．‎ ‎【分析】设这个两位数的十位数字为x，个位数字为y，等量关系为：十位数字与个位数字的和为8，两位数加上18=这个两位数的十位数字与个位数字对调后所组成的新两位数，列方程组求解．‎ ‎【解答】解：设这个两位数的十位数字为x，个位数字为y，‎ 由题意得，，‎ 解得：，‎ 则这个两位数为：35．‎ 故答案为：35．‎ ‎【点评】本题考查了二元一次方程组的应用，解答本题的关键是找出等量关系，根据等量关系列方程组求解．‎ ‎　‎ ‎15．已知x=‎2a+4，y=‎2a+3，如果用x表示y，则y=　x﹣1　．‎ ‎【考点】解二元一次方程．‎ ‎【专题】计算题．‎ ‎【分析】由x=‎2a+4，y=‎2a+3，两式相减，即可得出关于x与y的关系式，然后移项即可得出答案．‎ ‎【解答】解：由x=‎2a+4，y=‎2a+3，‎ 两式相减得：x﹣y=1，移项得：y=x﹣1．‎ 故答案为：x﹣1．‎ ‎【点评】本题考查了解二元一次方程，难度不大，关键是两式相减后建立关于x与y的关系式．‎ ‎　‎ 三、解答题 ‎16．解方程组．‎ ‎【考点】解二元一次方程组．‎ ‎【专题】计算题．‎ ‎【分析】方程组整理后两方程相减消去y求出x的值，进而求出y的值，即可确定出方程组的解．‎ ‎【解答】解：方程组整理得：，‎ ‎①﹣②得：2x=﹣6，‎ 即x=﹣3，‎ 将x=﹣3代入①，得：y=﹣，‎ 则方程组的解为．‎ ‎【点评】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：加减消元法与代入消元法．‎ ‎　‎ ‎17．某高校共有5个大餐厅和2个小餐厅．经过测试：同时开放1个大餐厅、2个小餐厅，可供1680名学生就餐；同时开放2个大餐厅、1个小餐厅，可供2280名学生就餐．‎ ‎（1）求1个大餐厅、1个小餐厅分别可供多少名学生就餐；‎ ‎（2）若7个餐厅同时开放，能否供全校的5300名学生就餐？请说明理由．‎ ‎【考点】二元一次方程组的应用．‎ ‎【分析】（1）根据题意可知本题的等量关系有，1个大餐厅容纳的学生人数+2个小餐厅容纳的学生人数=1680，2个大餐厅容纳的学生人数+1个小餐厅容纳的学生人数=2280．根据这两个等量关系，可列出方程组．‎ ‎（2）根据题（1）得到1个大餐厅和1个小餐厅分别可容纳学生的人数，可以求出5个大餐厅和2个小餐厅一共可容纳学生的人数，再和5300比较．‎ ‎【解答】解：（1）设1个大餐厅可供x名学生就餐，1个小餐厅可供y名学生就餐，根据题意，得 解这个方程组，得 答：1个大餐厅可供960名学生就餐，1个小餐厅可供360名学生就餐．‎ ‎（2）因为960×5+360×2=5520＞5300，‎ 所以如果同时开放7个餐厅，能够供全校的5300名学生就餐．‎ ‎【点评】本题考查二元一次方程的应用，属于比较基本的应用问题．注意根据题目给出的已知条件，找出合适的等量关系，列出方程组，再求解．‎ ‎　‎ ‎18． 甲对乙说：“当我的岁数是你现在的岁数时，你才4岁”．乙对甲说：“当我的岁数是你现在的岁数时，你将61岁”．请你算一算，甲、乙现在各多少岁．‎ ‎【考点】二元一次方程组的应用．‎ ‎【专题】年龄问题．‎ ‎【分析】根据题意，有“当我的岁数是你现在的岁数时，你才4岁”可得出：乙的年龄﹣两人的年龄差=4，‎ 由“当我的岁数是你现在的岁数时，你将61岁”，可得出：甲的年龄+两人的年龄差=61．由此列出方程组求解．‎ ‎【解答】解：设甲现在年龄x岁，乙现在年龄y岁，‎ 则，‎ 整理得 ‎①+②×2得3y=69，即y=23，‎ 把y=23代入②得x=42．‎ ‎∴原方程的解为．‎ 答：甲现在42岁，乙现在23岁．‎ ‎【点评】解题关键是弄清题意，合适的等量关系，直接设未知数，列出二元一次方程组求解．‎ ‎　‎ ‎19． 有甲乙两种铜和银的合金，甲种合金含银25%，乙种合金含银37.5%，现在要熔制含银30%的合金100千克，甲、乙两种合金各应取多少？‎ ‎【考点】二元一次方程组的应用．‎ ‎【专题】应用题．‎ ‎【分析】先设甲、乙两种合金各应取x千克和y千克，再根据混合物中某物质的质量=混合物的质量×混合物中该物质的质量分数进行求解即可得出答案．‎ ‎【解答】解：设需甲合金的质量为x千克，乙合金的质量为y千克，由题意得：‎ ‎，‎ 解得：．‎ 答：甲合金应取60千克，乙合金应取40千克．‎ ‎【点评】本题主要考查了二元一次方程组的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．本题用到的等量关系是混合物中某物质的质量=混合物的质量×混合物中该物质的质量分数．‎ ‎　‎ ‎20． 甲乙两地相距160千米，一辆汽车和一辆拖拉机从两地同时出发相向而行，1小时20分后相遇．相遇后，拖拉机继续前进，汽车在相遇处停留1小时后原速返回，在汽车再次出发半小时后追上了拖拉机，这时汽车、拖拉机从开始到现在各自行驶了多少千米？‎ ‎【考点】二元一次方程组的应用．‎ ‎【分析】设汽车的速度是x千米每小时，拖拉机速度y千米每小时，根据甲乙两地相距160千米1小时20分后相遇和拖拉机继续前进，汽车在相遇处停留1小时后原速返回，在汽车再次出发半小时后追上了拖拉机，列出方程，求出x，y的值，再根据路程=速度×时间即可得出答案．‎ ‎【解答】解：设汽车的速度是x千米每小时，拖拉机速度y千米每小时，根据题意得：‎ ‎，‎ 解得：，‎ 则汽车汽车行驶的路程是：（ +）×90=165（千米），‎ 拖拉机行驶的路程是：（ +）×30=85（千米）．‎ 答：汽车、拖拉机从开始到现在各自行驶了165千米和85千米．‎ ‎【点评】本题主要考查了二元一次方程组的应用的知识点，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．利用二元一次方程组求解的应用题一般情况下题中要给出2个等量关系，准确的找到等量关系并用方程组表示出来是解题的关键；本题用到的知识点是路程=速度×时间．‎ ‎　‎ ‎21． 如图，某化工厂与A，B两地有公路和铁路相连，这家工厂从A地购买一批每吨1 000元的原料运回工厂，制成每吨8 000元的产品运到B地．已知公路运价为1.5元/（吨•千米），铁路运价为1.2元/（吨•千米），这两次运输共支出公路运费15 000元，铁路运费97 200元，请计算这批产品的销售款比原料费和运输费的和多多少元？‎ ‎（1）根据题意，甲、乙两名同学分别列出尚不完整的方程组如下：‎ 甲：‎ 乙：‎ 根据甲，乙两名同学所列方程组，请你分别指出未知数x，y表示的意义，然后在等式右边的方框内补全甲、乙两名同学所列方程组．‎ 甲：x表示　产品的重量　，y表示　原料的重量　‎ 乙：x表示　产品销售额　，y表示　原料费　‎ ‎（2）甲同学根据他所列方程组解得x=300，请你帮他解出y的值，并解决该实际问题．‎ ‎【考点】二元一次方程组的应用．‎ ‎【分析】（1）仔细分析题意根据题目中的两个方程表示出x，y的值并补全方程组即可；‎ ‎（2）将x的值代入方程组即可得到结论．‎ ‎【解答】解：（1）甲：x表示产品的重量，y表示原料的重量，‎ 乙：x表示产品销售额，y表示原料费，‎ 甲方程组右边方框内的数分别为：15000，97200，乙同甲；‎ 则，‎ ‎．‎ ‎（2）将x=300代入原方程组解得y=400‎ ‎∴产品销售额为300×8000=2400000元 原料费为400×1000=400000元 ‎∴运费为15000+97200=112200元，‎ ‎∴2400000﹣（400000+112200）=1887800（元）‎ 答：这批产品的销售额比原料费和运费的和多1887800元．‎ ‎【点评】本题考查了二元一次方程组的应用，解题的关键是从题目中找到等量关系并写出表示出x、y所表示的实际意义．‎ ‎　‎ ‎ ‎