中考复习专题训练一次函数图像应用题 11页

中考复习专题训练：一次函数图像应用题 ‎1、有六个学生分成甲、乙两组（每组三个人），分乘两辆出租车同时从学校出发去距学校60km的博物馆参观，10分钟后到达距离学校12km处有一辆汽车出现故障，接着正常行驶的一辆车先把第一批学生送到博物馆再回头接第二批学生，同时第二批学生步行12km后停下休息10分钟恰好与回头接他们的小汽车相遇，当第二批学生到达博物馆时，恰好已到原计划时间．设汽车载人和空载时的速度不变，学生步行速度不变，汽车离开学校的路程s（千米）与汽车行驶时间t（分钟）之间的函数关系如图，假设学生上下车时间忽略不计．‎ ‎(1)原计划从学校出发到达博物馆的时间是　　 　分钟；‎ ‎(2)求汽车在回头接第二批学生途中的速度；‎ ‎(3)假设学生在步行途中不休息且步行速度每分钟减小0.04km，汽车载人时和空载时速度不变，问能否经过合理的安排，使得学生从学校出发全部到达目的地的时间比原计划时间早10分钟？如果能，请简要说出方案，并通过计算说明；如果不能，简要说明理由．‎ ‎2、我市某校根据规划设计，修建一条1200米长的校园道路。甲队单独施工5天后，为了能提前完成任务，邀请乙队加入施工，乙队的工作效率是甲队的，图中线段OA、AB分别表示甲队单独施工与两队合作施工所完成的工作量与施工天数之间的函数关系。‎ ‎(1)求甲队每天铺路多少米？‎ ‎(2)求图中线段AB所表示的函数关系式？‎ ‎(3)若甲队施工一天，需付工程款8000元，乙队施工一天需付工程款5000元，该工程计划在26天内完成，请你设计方案：在不超过计划天数的前提下，如何安排甲乙两队的施工天数(天数为正整数)，使完成该项工程的费用最省？‎ 第 11 页 共 11 页 ‎3、某客船往返于A、B两码头，在A、B间有旅游码头C．客船往返过程中，船在C、B处停留时间忽略不计，设客船离开码头A的距离s（千米）与航行的时间t（小时）之间的函数关系如图所示．根据图象提供的信息，解答下列问题：‎ ‎⑴船只从码头A→B，航行的速度为 千米/时；船只从码头B→A，航行的速度为 千米/时；‎ ‎⑵过点C作CH∥t轴，分别交AD、DF于点G、H，设AC=，GH=y，求出y与之间的函数关系式；‎ ‎⑶若旅游码头C设在离A码头30千米处， 一旅游团队在旅游码头C分两组行动，一组乘橡皮艇漂流而下，另一组乘船到达码头B后，立即返回．‎ ‎①求船只往返C、B两处所用的时间；‎ ‎②两组在途中相遇，求相遇时船只离旅游码头C有多远．‎ A C G H F ‎7.5‎ t（小时）‎ S(千米)‎ D B ‎90‎ E ‎3‎ ‎4．南宁市狮山公园计划在健身区铺设广场砖．现有甲、乙两个工程队参加竞标，甲工程队铺设广场砖的造价（元）与铺设面积的函数关系如图12所示；乙工程队铺设广场砖的造价（元）与铺设面积满足函数关系式：．‎ ‎（1）根据图12写出甲工程队铺设广场砖的造价（元）与铺设面积的函数关系式；‎ ‎（2）如果狮山公园铺设广场砖的面积为，那么公园应选择哪个工程队施工更合算？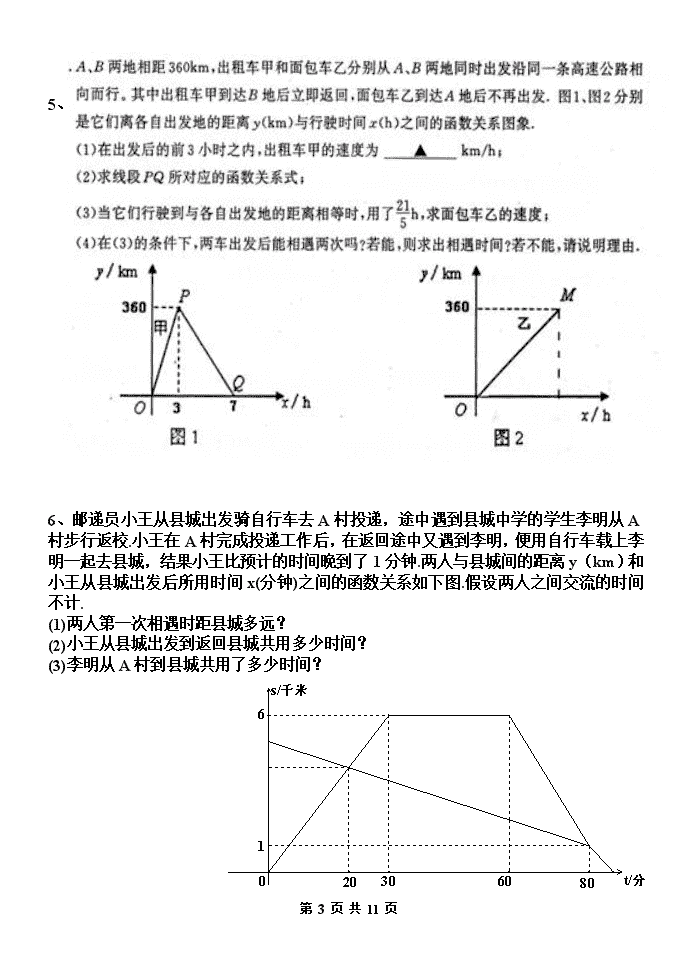‎ 图12‎ y元 ‎48000‎ ‎48000‎ ‎28000‎ ‎0‎ ‎500‎ ‎1000‎ 第 11 页 共 11 页 ‎5、‎ ‎6、邮递员小王从县城出发骑自行车去A村投递，途中遇到县城中学的学生李明从A村步行返校.小王在A村完成投递工作后，在返回途中又遇到李明，便用自行车载上李明一起去县城，结果小王比预计的时间晚到了1分钟.两人与县城间的距离y（km）和小王从县城出发后所用时间x(分钟)之间的函数关系如下图.假设两人之间交流的时间不计.‎ ‎(1)两人第一次相遇时距县城多远？‎ ‎(2)小王从县城出发到返回县城共用多少时间？‎ ‎(3)李明从A村到县城共用了多少时间？‎ 第 11 页 共 11 页 ‎4‎ ‎5‎ ‎300‎ ‎（小时）‎ ‎（千米）‎ O ‎7、已知A、B两地相距300千米，甲、乙两车同时从地出发，以各自的速度匀速往返两地．甲车先到达地，停留1小时后按原路返回．设两车行驶的时间为小时，离开地的距离是千米，如图是 与的函数图 ‎(1)计算甲、乙两车的速度；‎ ‎(2)几小时后两车相遇；‎ ‎(3)在从开始出发到两车相遇的过程中，设两车之间的距离为千米，乙车行驶的时间为 小时，求与之间的函数关系式．‎ ‎8、、两座城市之间有一条高速公路，甲、乙两辆汽车同时分别从这条路两端的入口处驶入，并始终在高速公路上正常行驶．甲车驶往城，乙车驶往城，甲车在行驶过程中速度始终不变．甲车距城高速公路入口处的距离（千米）与行驶时间（时）之间的关系如图．‎ ‎1‎ ‎2‎ ‎33‎ ‎43‎ ‎53‎ ‎60‎ ‎120‎ ‎180‎ ‎240‎ ‎300‎ ‎360‎ O ‎/千米 ‎/时 ‎(1)求关于的表达式；‎ ‎(2)已知乙车以60千米/时的速度匀速行驶，设行驶过程中，两车相距的路程为（千米）．请直接写出关于的表达式；‎ ‎(3)当乙车按（2）中的状态行驶与甲车相遇后，速度随即改为（千米/时）并保持匀速行驶，结果比甲车晚40分钟到达终点，求乙车变化后的速度．在下图中画出乙车离开城高速公路入口处的距离（千米）与行驶时间（时）之间的函数图象．‎ ‎9、‎ 第 11 页 共 11 页 ‎10、甲车从A地驶往C地，在C停留一段时间后，返回A地，乙车从B地经C地驶往A地，两车同时出发，相向而行，同时到达C地。设乙车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系。信息读取：‎ ‎(1)A、B两地之间的距离为_______km；甲车的速度_________；乙车的速度__________；请解释图中点D的实际意义是_________________________________；‎ ‎(2)求出当时，y与x之间的函数关系式，并在图中补全函数图象。‎ ‎11、甲、乙两城市之间开通了动车组高速列车．已知每隔2‎ 第 11 页 共 11 页 ‎ h有一列速度相同的动车组列车从甲城开往乙城．如图，OA是第一列动车组列车离开甲城的路程s（km）与运行时间t（h）的函数图象，BC是一列从乙城开往甲城的普通快车距甲城的路程s（km）与运行时间t（h）的函数图象．请根据图中的信息，解答下列问题：‎ ‎(1)从图象看，普通快车发车时间比第一列动车组列车发车时间 1 h(填”早”或”晚”)，‎ 点B的纵坐标600的实际意义是 ；‎ A B C M O ‎2‎ ‎4‎ ‎6‎ ‎1‎ ‎200‎ ‎400‎ ‎600‎ s/km t/h ‎(2)请直接在图中画出第二列动车组列车离开甲城的路程s（km）与时间t（h）的函数图象；‎ ‎(3)若普通快车的速度为100 km/h，‎ ‎①求BC的表达式，并写出自变量的取值范围；‎ ‎②第二列动车组列车出发多长时间后与普通快车相遇？‎ ‎③请直接写出这列普通快车在行驶途中与迎面而来的相邻两列动车组列车相遇的时间间隔．‎ ‎12、在一次远足活动中，小聪由甲地步行到乙地后原路返回，小明由甲地步行到乙地后原路返回，到达途中的丙地时发现物品可能遗忘在乙地，于是从丙返回乙地，然后沿原路返回．两人同时出发，步行过程中保持匀速．设步行的时间为t（h），两人离甲地的距离分别为S1（km）和S2(km)，图中的折线分别表示S1、S2与t之间的函数关系．‎ ‎(1)甲、乙两地之间的距离为 km，乙、丙两地之间的距离为 km；‎ ‎(2)分别求出小明由甲地出发首次到达乙地及由乙地到达丙地所用的时间．‎ ‎(3)求图中线段AB所表示的S2与t间的函数关系式，并写出自变量t的取值范围．‎ ‎2‎ t(h)‎ O A B C S(km)‎ ‎10‎ ‎8‎ ‎（第25题图）‎ ‎13、甲、乙两地相距720‎ 第 11 页 共 11 页 ‎ km，一列快车和一列慢车都从甲地驶往乙地，慢车先行驶1小时后，快车才开始行驶．已知快车的速度是120 km/h，以快车开始行驶计时，设时间为x（h），两车之间的距离为y（km），图中的折线是y与x之间的函数关系的部分图象．‎ 根据函数图象解决以下问题：‎ ‎(1)慢车的速度是 ，点B的坐标是 ；‎ ‎(2)求线段AB所表示的y与x之间的函数关系式；‎ ‎(3)试在图中补全点B以后的图象．‎ y∕km ‎2 ‎ x∕h O ‎12‎ A B ‎80‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎14、(本小题满分8分）‎ 甲、乙两人骑自行车前往A地，他们距A地的路程s（km）与行驶时间t（h）之间的关系如图所示，请根据图象所提供的信息解答下列问题：‎ ‎（1）甲、乙两人的速度各是多少？ ‎ ‎（2）求出甲距地的路程与行驶时间之间的函数关系式．‎ ‎（3）在什么时间段内乙比甲离地更近？‎ ‎0‎ ‎1‎ ‎2‎ ‎2.5‎ ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ ‎60‎ 乙 甲 ‎15．（本小题满分8分）‎ 第 11 页 共 11 页 甲、乙两辆汽车沿同一路线赶赴距出发地480千米的目的地，乙车比甲车晚出发2小时（从甲车出发时开始计时）．图中折线、线段分别表示甲、乙两车所行路程（千米）与时间（小时）之间的函数关系对应的图象（线段表示甲出发不足2小时因故停车检修）．请根据图象所提供的信息，解决如下问题：‎ ‎（1）求乙车所行路程与时间的函数关系式；‎ ‎（2）求两车在途中第二次相遇时，它们距出发地的路程；‎ ‎（3）乙车出发多长时间，两车在途中第一次相遇？（写出解题过程）‎ A O D P B F G E y（千米）‎ x（小时）‎ ‎480‎ ‎6‎ ‎8‎ ‎10‎ ‎2‎ ‎4.5‎ ‎16、（本小题满分7分）为迎接2008年北京奥运会，某学校组织了一次野外长跑活动，参加长跑的同学出发后，另一些同学从同地骑自行车前去加油助威。如图，线段L1，L2分别表示长跑的同学和骑自行车的同学行进的路程y（千米）随时间x（分钟）变化的函数图象。根据图象，解答下列问题：‎ ‎（1）分别求出长跑的同学和骑自行车的同学的行进路程y与时间x的函数表达式；‎ ‎（2）求长跑的同学出发多少时间后，骑自行车的同学就追上了长跑的同学？‎ 第 11 页 共 11 页 参考答案 ‎1.（1）100 （2）1.8km/min (3)能够合理安排.　 ‎ 方案：从故障点开始，在第二批学生步行的同时出租车先把第一批学生送到途中放下，让他们步行，再回头接第二批学生，当两批学生同时到达博物馆，时间可提前10分钟． ………6分 理由：设从故障点开始第一批学生乘车t1分钟，汽车回头时间为t2分钟，由题意得：‎ ‎.解得：.　 ………7分 从出发到达博物馆的总时间为：10+2×32+16=90(分钟) .‎ 即时间可提前100-90=10(分钟) . 　 ………8分 ‎5.‎ ‎6.‎ ‎（1）甲车速度为100千米/小时，‎ 乙车速度为60千米/小时 ‎ ‎(2)小时两车相遇 ‎ 第 11 页 共 11 页 法一：= 法二：联立两个函数关系式，解得 ‎ ‎(3)当时，，当时，，当时， ‎ ‎7.（1）方法一：由图知是的一次函数，设 ‎ 图象经过点（0，300），（2，120），∴2分 解得3分 ‎∴即关于的表达式为 ‎ 方法二：由图知，当时，；时，‎ 所以，这条高速公路长为300千米．　　　　　甲车2小时的行程为300－120=180（千米）．‎ ‎∴甲车的行驶速度为180÷2=90（千米／时）．‎ ‎∴关于的表达式为（）．‎ ‎（2） ‎ ‎（3）在中．当时，即甲乙两车经过2小时相遇． ‎ ‎1‎ ‎2‎ ‎33‎ ‎43‎ ‎53‎ ‎60‎ ‎120‎ ‎180‎ ‎240‎ ‎300‎ ‎360‎ O ‎/千米 ‎/时 在中，当．‎ 所以，相遇后乙车到达终点所用的时间为（小时）．‎ 乙车与甲车相遇后的速度 ‎（千米/时）．∴（千米/时）．‎ 乙车离开城高速公路入口处的距离（千米）与行驶时间 ‎（时）之间的函数图象如图所示． ‎ ‎9.（1）960；　100km/h；　60km/h； 乙车行驶11小时后被甲车追上； ‎ ‎（2）y＝40(x-11)＝40x－440， 过(11,0)、(16,200)的线段； ‎ ‎11.（1）10，2 ‎ ‎（2）解：v2＝(10＋2)÷1＝12，t1＝10÷12＝，t2＝2÷12＝，‎ ‎∴小明由甲地出发首次到达乙地用了小时，由乙地到达丙地用了小时． ‎ ‎（3）解：设线段AB所表示的S2与之间的函数关系式为S2＝kt＋b()．由（1）可知点A、B的坐标为A(，10)，B(1，8)，代入，得 解得：，∴S2＝－12t＋20‎ 第 11 页 共 11 页 ‎ ()‎ ‎12.解：（1）80km/h ， (6,160) ‎ y∕km ‎2 ‎ x∕h O ‎12‎ A B ‎80‎ ‎4‎ ‎6‎ ‎8‎ ‎10‎ ‎(2) 设线段AB所表示的y与x之间的函数关系式为:‎ y＝kx＋b（k≠0），根据题意得: ‎ 解得：k＝40,b＝－80 ‎ ‎∴y＝40x－80 ‎ ‎（3）见图 ‎ 第 11 页 共 11 页